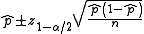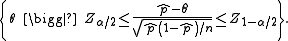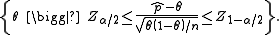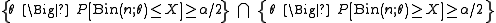Binomial proportion confidence interval
Encyclopedia
In statistics
, a binomial proportion confidence interval is a confidence interval
for a proportion in a statistical population
. It uses the proportion estimated in a statistical sample and allows for sampling error
. There are several formulas for a binomial confidence interval, but all of them rely on the assumption of a binomial distribution. In general, a binomial distribution applies when an experiment is repeated a fixed number of times, each trial of the experiment has two possible outcomes (labeled arbitrarily success and failure), the probability of success is the same for each trial, and the trials are statistically independent.
A simple example of a binomial distribution is the set of various possible outcomes, and their probabilities, for the number of heads observed when a (not necessarily fair) coin is flipped ten times. The observed binomial proportion is the fraction of the flips which turn out to be heads. Given this observed proportion, the confidence interval for the true proportion innate in that coin is a range of possible proportions which may contain the true proportion. A 95% confidence interval for the proportion, for instance, will contain the true proportion 95% of the times that the procedure for constructing the confidence interval is employed.
There are several ways to compute a confidence interval for a binomial proportion. The normal approximation interval is the simplest formula, and the one introduced in most basic Statistics classes and textbooks. This formula, however, is based on an approximation that does not always work well. Several competing formulas are available that perform better, especially for situations with a small sample size and a proportion very close to zero or one. The choice of interval will depend on how important it is to use a simple and easy-to-explain interval versus the desire for better accuracy.
. The formula is
where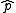 is the proportion of successes in a Bernoulli trial
is the proportion of successes in a Bernoulli trial
process estimated from the statistical sample,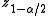 is the
is the 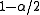 percentile
percentile
of a standard normal distribution, is the error percentile and n is the sample size. For example, for a 95% confidence level the error (
is the error percentile and n is the sample size. For example, for a 95% confidence level the error ( ) is 5%, so
) is 5%, so 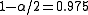 and
and 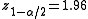 .
.
The central limit theorem
applies well to a binomial distribution, even with a sample size less than 30, as long as the proportion is not too close to 0 or 1. For very extreme probabilities, though, a sample size of 30 or more may still be inadequate. The normal approximation fails totally when the sample proportion is exactly zero or exactly one. A frequently cited rule of thumb is that the normal approximation works well as long as np > 5 and n(1 − p) > 5; see however Brown et al. 2001. In practice there is little reason to use this method rather than one of the other, better performing, methods.
An important theoretical derivation of this confidence interval involves the inversion of a hypothesis test. Under this formulation, the confidence interval represents those values of the population parameter that would have large p-values if they were tested as a hypothesized population proportion. The collection of values,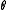 , for which the normal approximation is valid can be represented as
, for which the normal approximation is valid can be represented as
Since the test in the middle of the inequality is a Wald test
, the normal approximation interval is sometimes called the Wald
interval, but Pierre-Simon Laplace
described it 1812 in Théorie analytique des probabilités (pag. 283).
is closer to the nominal value) over the normal approximation interval and was first developed by Edwin Bidwell Wilson
(1927).
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, a binomial proportion confidence interval is a confidence interval
Confidence interval
In statistics, a confidence interval is a particular kind of interval estimate of a population parameter and is used to indicate the reliability of an estimate. It is an observed interval , in principle different from sample to sample, that frequently includes the parameter of interest, if the...
for a proportion in a statistical population
Statistical population
A statistical population is a set of entities concerning which statistical inferences are to be drawn, often based on a random sample taken from the population. For example, if we were interested in generalizations about crows, then we would describe the set of crows that is of interest...
. It uses the proportion estimated in a statistical sample and allows for sampling error
Sampling error
-Random sampling:In statistics, sampling error or estimation error is the error caused by observing a sample instead of the whole population. The sampling error can be found by subtracting the value of a parameter from the value of a statistic...
. There are several formulas for a binomial confidence interval, but all of them rely on the assumption of a binomial distribution. In general, a binomial distribution applies when an experiment is repeated a fixed number of times, each trial of the experiment has two possible outcomes (labeled arbitrarily success and failure), the probability of success is the same for each trial, and the trials are statistically independent.
A simple example of a binomial distribution is the set of various possible outcomes, and their probabilities, for the number of heads observed when a (not necessarily fair) coin is flipped ten times. The observed binomial proportion is the fraction of the flips which turn out to be heads. Given this observed proportion, the confidence interval for the true proportion innate in that coin is a range of possible proportions which may contain the true proportion. A 95% confidence interval for the proportion, for instance, will contain the true proportion 95% of the times that the procedure for constructing the confidence interval is employed.
There are several ways to compute a confidence interval for a binomial proportion. The normal approximation interval is the simplest formula, and the one introduced in most basic Statistics classes and textbooks. This formula, however, is based on an approximation that does not always work well. Several competing formulas are available that perform better, especially for situations with a small sample size and a proportion very close to zero or one. The choice of interval will depend on how important it is to use a simple and easy-to-explain interval versus the desire for better accuracy.
Normal approximation interval
The simplest and most commonly used formula for a binomial confidence interval relies on approximating the binomial distribution with a normal distribution. This approximation is justified by the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
. The formula is
where
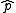 is the proportion of successes in a Bernoulli trial
is the proportion of successes in a Bernoulli trialBernoulli trial
In the theory of probability and statistics, a Bernoulli trial is an experiment whose outcome is random and can be either of two possible outcomes, "success" and "failure"....
process estimated from the statistical sample,
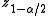 is the
is the 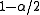 percentile
percentilePercentile rank
The percentile rank of a score is the percentage of scores in its frequency distribution that are the same or lower than it. For example, a test score that is greater than 75% of the scores of people taking the test is said to be at the 75th percentile....
of a standard normal distribution,
 is the error percentile and n is the sample size. For example, for a 95% confidence level the error (
is the error percentile and n is the sample size. For example, for a 95% confidence level the error ( ) is 5%, so
) is 5%, so 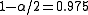 and
and 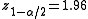 .
.The central limit theorem
Central limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
applies well to a binomial distribution, even with a sample size less than 30, as long as the proportion is not too close to 0 or 1. For very extreme probabilities, though, a sample size of 30 or more may still be inadequate. The normal approximation fails totally when the sample proportion is exactly zero or exactly one. A frequently cited rule of thumb is that the normal approximation works well as long as np > 5 and n(1 − p) > 5; see however Brown et al. 2001. In practice there is little reason to use this method rather than one of the other, better performing, methods.
An important theoretical derivation of this confidence interval involves the inversion of a hypothesis test. Under this formulation, the confidence interval represents those values of the population parameter that would have large p-values if they were tested as a hypothesized population proportion. The collection of values,
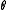 , for which the normal approximation is valid can be represented as
, for which the normal approximation is valid can be represented asSince the test in the middle of the inequality is a Wald test
Wald test
The Wald test is a parametric statistical test named after Abraham Wald with a great variety of uses. Whenever a relationship within or between data items can be expressed as a statistical model with parameters to be estimated from a sample, the Wald test can be used to test the true value of the...
, the normal approximation interval is sometimes called the Wald
Abraham Wald
- See also :* Sequential probability ratio test * Wald distribution* Wald–Wolfowitz runs test...
interval, but Pierre-Simon Laplace
Pierre-Simon Laplace
Pierre-Simon, marquis de Laplace was a French mathematician and astronomer whose work was pivotal to the development of mathematical astronomy and statistics. He summarized and extended the work of his predecessors in his five volume Mécanique Céleste...
described it 1812 in Théorie analytique des probabilités (pag. 283).
Wilson score interval
The Wilson interval is an improvement (the actual coverage probabilityCoverage probability
In statistics, the coverage probability of a confidence interval is the proportion of the time that the interval contains the true value of interest. For example, suppose our interest is in the mean number of months that people with a particular type of cancer remain in remission following...
is closer to the nominal value) over the normal approximation interval and was first developed by Edwin Bidwell Wilson
Edwin Bidwell Wilson
Edwin Bidwell Wilson was an American mathematician and polymath. He was the sole protégé of Yale's physicist Josiah Willard Gibbs and was mentor to MIT economist Paul Samuelson. He received his AB from Harvard College in 1899 and his PhD from Yale University in 1901, working under Gibbs.E.B...
(1927).
-
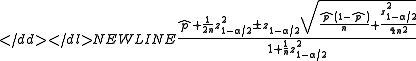
This interval has good properties even for a small number of trials and/or an extreme probability. The center of the Wilson interval
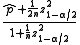
can be shown to be a weighted average of and
and 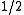 , with
, with 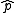 receiving greater weight as the sample size increases. For the 95% interval, the Wilson interval is nearly identical to the normal approximation interval using
receiving greater weight as the sample size increases. For the 95% interval, the Wilson interval is nearly identical to the normal approximation interval using  instead of
instead of 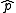 .
.
The Wilson interval can be derived from
by solving for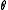 .
.
The test in the middle of the inequality is a score testScore testA score test is a statistical test of a simple null hypothesis that a parameter of interest \theta isequal to some particular value \theta_0. It is the most powerful test when the true value of \theta is close to \theta_0. The main advantage of the Score-test is that it does not require an...
, so the Wilson interval is sometimes called the Wilson score interval.
Clopper-Pearson interval
The Clopper-Pearson interval is an early and very common method for calculating binomial confidence intervals. This is often called an 'exact' method, but that is because it is based on the cumulative probabilities of the binomial distribution (i.e. exactly the correct distribution rather than an approximation), but the intervals are not exact in the way that one might assume: the discontinuous nature of the binomial distribution precludes any interval with exact coverage for all population proportions. The Clopper-Pearson interval can be written as
where X is the number of successes observed in the sample and Bin(n; θ) is a binomial random variable with n trials and probability of success θ.
Because of a relationship between the cumulative binomial distribution and the beta distribution, the Clopper-Pearson interval is sometimes presented in an alternate format that uses percentiles from the beta distribution. The beta distribution is, in turn, related to the F-distribution so a third formulation of the Clopper-Pearson interval uses F percentiles.
The Clopper-Pearson interval is an exact interval since it is based directly on the binomial distribution rather than any approximation to the binomial distribution. This interval never has less than the nominal coverage for any population proportion, but that means that it is usually conservative. For example, the true coverage rate of a 95% Clopper-Pearson interval may be well above 95%, depending on n and θ. Thus the interval may be wider than it needs to be to achieve 95% confidence. In contrast, it is worth noting that other confidence bounds may be narrower than their nominal confidence with, i.e., the Normal Approximation (or "Standard") Interval, Wilson Interval, Agresti-Coull Interval, etc., with a nominal coverage of 95% may in fact cover less than 95%.
Agresti-Coull Interval
The Agresti-Coull interval is another approximate binomial confidence interval.
Given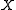 successes in
successes in  trials, define
trials, define
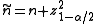
and
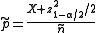
Then, a confidence interval for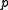 is given by
is given by
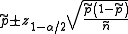
where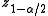 is the
is the 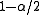 percentile of a standard normal distribution, as before. For example, for a 95% confidence interval, let
percentile of a standard normal distribution, as before. For example, for a 95% confidence interval, let 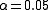 , so
, so  = 1.96 and
= 1.96 and 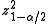 = 3.84. If we use 2 instead of 1.96 for
= 3.84. If we use 2 instead of 1.96 for 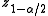 , this is the "add 2 successes and 2 failures" interval in
, this is the "add 2 successes and 2 failures" interval in
Jeffreys interval
The 'Jeffreys interval' is the Bayesian credible intervalCredible intervalIn Bayesian statistics, a credible interval is an interval in the domain of a posterior probability distribution used for interval estimation. The generalisation to multivariate problems is the credible region...
obtained when using the non-informative Jeffreys priorJeffreys priorIn Bayesian probability, the Jeffreys prior, named after Harold Jeffreys, is a non-informative prior distribution on parameter space that is proportional to the square root of the determinant of the Fisher information:...
for the binomial proportion . The Jeffreys prior for this problem is a Beta distribution with parameters . After observing successes in trials, the posterior distribution for is a Beta distribution with parameters . When and , the Jeffreys interval is taken to be the equal-tailed
posterior probability interval, i.e. the and quantiles of a Beta distribution with parameters
. These quantiles need to be computed numerically. In order to avoid the
coverage probability tending to zero when or , when the upper limit is calculated as before but the lower limit is set to 0, and when the lower limit is calculated as before but the upper limit is set to 1.
Comparison of different intervals
There are several research papers that compare these and other confidence intervals for the binomial proportion. A good starting point is Agresti and Coull (1998) or Ross (2003) which point out that exact methods such as the Clopper-Pearson interval may not work as well as certain approximations. But it is still used today for many studies.
See also
- Coverage probabilityCoverage probabilityIn statistics, the coverage probability of a confidence interval is the proportion of the time that the interval contains the true value of interest. For example, suppose our interest is in the mean number of months that people with a particular type of cancer remain in remission following...
- Estimation theoryEstimation theoryEstimation theory is a branch of statistics and signal processing that deals with estimating the values of parameters based on measured/empirical data that has a random component. The parameters describe an underlying physical setting in such a way that their value affects the distribution of the...
- Krichevsky–Trofimov estimatorKrichevsky–Trofimov estimatorIn information theory, given an unknown stationary source π with alphabet A, and a sample w from π, the Krichevsky–Trofimov estimator produces an estimate πi of the probabilities of each symbol i ∈ A...
- Rule of threeRule of three (medicine)In the statistical analysis of clinical trials, the rule of three states that if no major adverse events occurred in a group of n people, there can be 95% confidence that the chance of major adverse events is less than one in n / 3...
Further reading
- Reiczigel J. (2003) Confidence intervals for the binomial parameter: some new considerations. Statistics in Medicine, 22, 611–621.
-