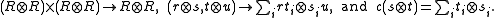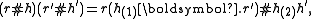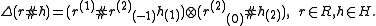Braided Hopf algebra
Encyclopedia
In mathematics
a braided Hopf algebra is a Hopf algebra
in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.
The notion should not be confused with quasitriangular Hopf algebra.
 if
if
A braided bialgebra in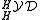 is called a braided Hopf algebra, if there is a morphism
is called a braided Hopf algebra, if there is a morphism 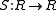 of Yetter–Drinfel'd modules such that
of Yetter–Drinfel'd modules such that
where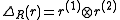 in slightly modified Sweedler notation
in slightly modified Sweedler notation
– a change of notation is performed in order to avoid confusion in Radford's biproduct below.
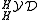 there exists a natural Hopf algebra
there exists a natural Hopf algebra 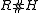 which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn Majid
which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn Majid
, who called it bosonization.
As a vector space,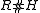 is just
is just 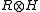 . The algebra structure of
. The algebra structure of 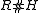 is given by
is given by
where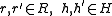 ,
, 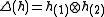 (Sweedler notation
(Sweedler notation
) is the coproduct of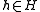 , and
, and 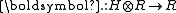 is the left action of H on R. Further, the coproduct of
is the left action of H on R. Further, the coproduct of 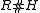 is determined by the formula
is determined by the formula
Here denotes the coproduct of r in R, and
denotes the coproduct of r in R, and 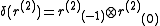 is the left coaction of H on
is the left coaction of H on 
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
a braided Hopf algebra is a Hopf algebra
Hopf algebra
In mathematics, a Hopf algebra, named after Heinz Hopf, is a structure that is simultaneously an algebra and a coalgebra, with these structures' compatibility making it a bialgebra, and that moreover is equipped with an antiautomorphism satisfying a certain property.Hopf algebras occur naturally...
in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.
The notion should not be confused with quasitriangular Hopf algebra.
Definition
Let H be a Hopf algebra over a field k, and assume that the antipode of H is bijective. A Yetter–Drinfel'd module R over H is called a braided bialgebra in the Yetter–Drinfel'd category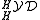 if
if
-
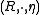 is a unital associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
is a unital associative algebraAssociative algebraIn mathematics, an associative algebra A is an associative ring that has a compatible structure of a vector space over a certain field K or, more generally, of a module over a commutative ring R...
, where the multiplication map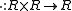 and the unit
and the unit 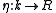 are maps of Yetter–Drinfel'd modules,
are maps of Yetter–Drinfel'd modules, -
 is a coassociative coalgebraCoalgebraIn mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
is a coassociative coalgebraCoalgebraIn mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
with counit , and both
, and both 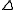 and
and  are maps of Yetter–Drinfel'd modules,
are maps of Yetter–Drinfel'd modules, - the maps
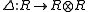 and
and  are algebra maps in the category
are algebra maps in the category 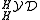 , where the algebra structure of
, where the algebra structure of 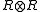 is determined by the unit
is determined by the unit 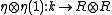 and the multiplication map
and the multiplication map
-
-
- Here c is the canonical braiding in the Yetter–Drinfel'd category
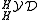 .
.
A braided bialgebra in
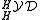 is called a braided Hopf algebra, if there is a morphism
is called a braided Hopf algebra, if there is a morphism 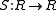 of Yetter–Drinfel'd modules such that
of Yetter–Drinfel'd modules such that
-
-
 for all
for all 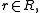
-
where
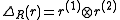 in slightly modified Sweedler notation
in slightly modified Sweedler notationCoalgebra
In mathematics, coalgebras or cogebras are structures that are dual to unital associative algebras. The axioms of unital associative algebras can be formulated in terms of commutative diagrams...
– a change of notation is performed in order to avoid confusion in Radford's biproduct below.
Examples
- Any Hopf algebra is also a braided Hopf algebra over
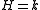
- A super Hopf algebra is nothing but a braided Hopf algebra over the group algebraGroup ringIn algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
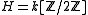 .
. - The tensor algebraTensor algebraIn mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
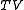 of a Yetter–Drinfeld module
of a Yetter–Drinfeld module 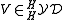 is always a braided Hopf algebra. The coproduct
is always a braided Hopf algebra. The coproduct 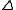 of
of  is defined in such a way that the elements of V are primitive, that is
is defined in such a way that the elements of V are primitive, that is
-
- The counit
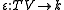 then satisfies the equation
then satisfies the equation 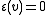 for all
for all 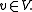
- The universal quotient of
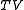 , that is still a braided Hopf algebra containing
, that is still a braided Hopf algebra containing 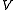 as primitive elements is called the Nichols algebra. They take the role of quantum Borel algebras in the classification of pointed Hopf algebras, analogously to the classical Lie algebra case.
as primitive elements is called the Nichols algebra. They take the role of quantum Borel algebras in the classification of pointed Hopf algebras, analogously to the classical Lie algebra case.
- The universal quotient of
Radford's biproduct
For any braided Hopf algebra R in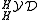 there exists a natural Hopf algebra
there exists a natural Hopf algebra 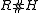 which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn Majid
which contains R as a subalgebra and H as a Hopf subalgebra. It is called Radford's biproduct, named after its discoverer, the Hopf algebraist David Radford. It was rediscovered by Shahn MajidShahn Majid
Born in 1960 in Patna, Bihar, India Shahn Majid is an English pure mathematician and theoretical physicist, trained at Cambridge University and Harvard and since 2001 a Professor of Mathematics at the School of Mathematical Sciences, Queen Mary, University of London.Majid is best known for his...
, who called it bosonization.
As a vector space,
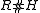 is just
is just 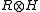 . The algebra structure of
. The algebra structure of 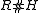 is given by
is given by
where
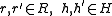 ,
, 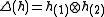 (Sweedler notation
(Sweedler notationCoproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
) is the coproduct of
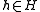 , and
, and 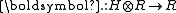 is the left action of H on R. Further, the coproduct of
is the left action of H on R. Further, the coproduct of 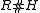 is determined by the formula
is determined by the formula
Here
 denotes the coproduct of r in R, and
denotes the coproduct of r in R, and 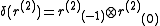 is the left coaction of H on
is the left coaction of H on