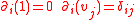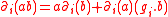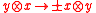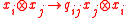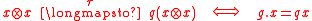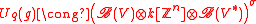Nichols algebra
Encyclopedia
The Nichols algebra of a braided vector space
(with the braiding often induced by a finite group) is a braided Hopf algebra
which is denoted by
and named after the mathematician Warren Nichols. It takes the role of quantum Borel part of a pointed Hopf algebra such as a quantum groups and their well known finite-dimensional truncations. Nichols algebras can immediately be used to write down new such quantum groups by using the Radford biproduct
Susan Montgomory asked to classify. which finite groups admit at all finite dimensional indecomposable Nichols algebras over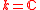
. The answering of this question, moreover the classification of all such Nichols algebras and even all associated quantum groups (see Application) is recently progressing rapidly, although still much is open: The case of an abelian group has been solved 2005, but otherwise this phenomenon seems to be a very rare occasion, with a handfull examples known and powerful negation criteria established (see below).
The finite dimensional theory is greatly governed by a theory of root system
s and Dynkin diagrams, strikingly similar to those of semisimple Lie algebras.. A comprehensive introduction is found in the lecture of Heckenberger
. This is especially a braided vectorspace, see Braided monoidal category.
The tensor algebra
of a Yetter–Drinfeld module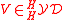 
is always a Braided Hopf algebra
. The coproduct
of 
is defined in such a way that the elements of 
are primitive, that is
As an example, all universal envelopings
of Lie algebras are (trivially braided) quotients thereof for
by Serre relations: The basis consists of derivational elements (=primitives), the higher powers usually solemnly of higher derivations and there are no further quotients still preserving V ("universal"). In the braided context, the "true" enveloping turns out to be often much smaller:
(note that in the further development of the theory, see below, the Nichols algebra takes rather the role of the quantum Borel part of the enveloping!)
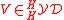. There exists a largest ideal
of
with the following properties:
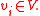(i.e. coaction/graduation 
) one may define skew derivations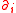 
, using the universal property of the tensor algebra:
Then the Nichols algebra is the quotient of TV by the largest homogeneous ideal which contains no constants and is invariant under all derivations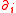
.
This ideal is larger (and in some cases strictly larger) than the ideal generated by the intersection of
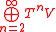with the kernels of the skew derivations 
.
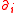over the Group Hopf algebra
with the Cyclic group
multiplicatively denoted (as usual in algebra) and generated by some g.
Then, depending on the sign choice, the Nichols algebras are:
Note that the first is as expected (the non-braided case), while the second has been truncated to the point that it's finite dimensional! Similarly,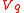
over a higher cyclic group with g acting by some 
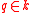has Nichols algebra 
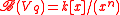if 
is a primitive n-th root of unity, and 
otherwise.
(from a physical perspective, the
corresponds to a boson, while 
represents a fermion restricted by Pauli exclusion principle
; an analogy that repeats when considering braided commutators, being (anti)commutators in these cases, see also Supersymmetry as a quantum group
and discussion)
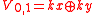over the group Hopf algebra
with the Klein four group multiplicatively denoted and generated by some g,h.
Then, depending on the sign choice, the Nichols algebras are of dimension 4 and 8 (they appear in the classification under
):
There one can see the striking resemblance to Semisimple Lie algebras: In the first case, the braided commutator
[x,y] (here: anticommutator) is zero, while in the second, the root string
is longer [x,[x,y]] = 0. Hence these two belong to Dynkin diagrams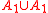
and 
.
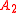One also constructs examples with even longer root strings
corresponding to Dynkin diagrams 
(but as well no higher ones!)
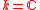are known so far. It is known that in this case each irreducible Yetter–Drinfel'd module 
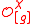corresponds to Conjugacy class
of the group (together with a irreducible representation of the centralizer
of g). An arbitrary Yetter–Drinfel'd module is a direct sum
of such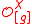
, the number of summands is called rank; each summand corresponds to anode in the Dynkin diagram (see below). Note that for the abelian groups as above, the irreducible summands are 1-dimensional, hence rank and dimension coinncide!
Some more examples are found e.g. in the "zoo" on M. Grana's Webpace page (please add more information, see discussion).
Recently, a family of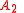
example of rank 2 over extensions of 
has been constructed
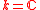were classified by Istvan Heckenberger in the years 2004–2005 by classifying arithmetic root system
s and generalized Dynkin diagrams; where already Kharchenko had proven them to posess a Poincare–Birkhoff–Witt basis
of iterated (braided) commutators. The only information one requires is the braiding matrix, which is diagonal in this setting (see examples above)
While mostly only the classical Cartan-cases appear, there are several exotic diagrams possible for small primes, such as a triangle
In these cases the Weyl reflections
of one diagram may not land in the "same" diagram, but a so-called Weyl equivalent. This is also the exact reason, that these exotic cases possess a Weyl-groupoid
instead of a usual group (picture?).
This ansatz puts sometimes strong conditions especially on the braiding
of any
-graded element 
with itself (e.g the first example above shows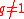 
). Note that because 
is central in the centralizer, it acts on the irreducible representation by a scalar as a consequence of the Schur lemma; hence this selfbraiding resp. 1-dim sub-Yetter-Drinfel'd-module / braided vectorspace / 1-dim subrack is diagonal
It is usually used to excludes
e.g. of being of odd order and/or 
of high dimension:
oid and a Poincare–Birkhoff–Witt basis
of iterated (braided) commutators
Immediate consequences are implied for rank 2 Nichols algebras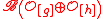
which g, h discommuting; then:
This implies roughly, that finite dimensional Nichols algebras over nonabelian groups have to be (if at all) of very low rank.
A specific case where this is highly successful is type D, i.e. for
in this case the Nichols algebra of the subrack is infinite dimensional and so is the entire Nichols algebra
Usually a large amount of conjugacy classes ae of type D ("not commutative enough"), while the others tend to posess sufficient abelian subracks and can be excluded by their consideration. Several cases have to be done by-hand. Note that the open cases tend to have very small centralizers (usually cyclic) and representations
(usually the 1-dimensional sign representation). Significant exceptions are the conjugacy classes of order 16, 32 having as centralizers p-groups
of order 2048 resp. 128 and currently no restrictions on
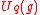and their well known truncations for q a root of unity decompose just like an ordinary Semisimple Lie algebra into E´s (Borel part), dual F´s and K´s (Cartan algebra):
Here, as in the classical theory V is a vectorspace of dimension n (the rank of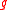
) spanned by the E´s, and 
(a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. See cit. loc. for an exotic example with 4 parts of type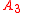 
.
The classification roughly reduces a given hypothetical example to a Radford biproduct
of the (coradical-) group and the (connected-) part, which contains the Nichols algebra, by taking the corresponding "graded object" (killing all linkings). With the knowledge from the classification of finite dimensional Nichols algebras above, the authors prove no additional elements to appear in the connected part (generation in degree 1), and finally describe all possible liftings as "dotted lines" in generalized Dynkin diagrams.
Recently, this correspondence has been greatly extended to identify certain so-called coideal subalgebras to be in 1:1 correspondence to the Weyl group
, which has been conjectued as "numercal coincidence" earlier and proven in certain cases by-hand.
Braided vector space
In mathematics, a braided vectorspace \;V is a vectorspace together with an additional structure map \tau\; symbolizing interchanging of two vector tensor copies:such that the Yang–Baxter equation is fulfilled...
(with the braiding often induced by a finite group) is a braided Hopf algebra
Braided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
which is denoted by
and named after the mathematician Warren Nichols. It takes the role of quantum Borel part of a pointed Hopf algebra such as a quantum groups and their well known finite-dimensional truncations. Nichols algebras can immediately be used to write down new such quantum groups by using the Radford biproductBraided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
Susan Montgomory asked to classify. which finite groups admit at all finite dimensional indecomposable Nichols algebras over
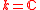. The answering of this question, moreover the classification of all such Nichols algebras and even all associated quantum groups (see Application) is recently progressing rapidly, although still much is open: The case of an abelian group has been solved 2005, but otherwise this phenomenon seems to be a very rare occasion, with a handfull examples known and powerful negation criteria established (see below). The finite dimensional theory is greatly governed by a theory of root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s and Dynkin diagrams, strikingly similar to those of semisimple Lie algebras.. A comprehensive introduction is found in the lecture of Heckenberger
Definition
Consider a Yetter–Drinfel'd module V in the Yetter–Drinfel'd category. This is especially a braided vectorspace, see Braided monoidal category.The tensor algebra
Tensor algebra
In mathematics, the tensor algebra of a vector space V, denoted T or T•, is the algebra of tensors on V with multiplication being the tensor product...
of a Yetter–Drinfeld module 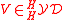is always a Braided Hopf algebraBraided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
. The coproduct
of is defined in such a way that the elements of are primitive, that is
-
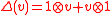for all 
- The counit
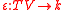then satisfies the equation 
for all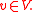 
As an example, all universal envelopings
Universal enveloping algebra
In mathematics, for any Lie algebra L one can construct its universal enveloping algebra U. This construction passes from the non-associative structure L to a unital associative algebra which captures the important properties of L.Any associative algebra A over the field K becomes a Lie algebra...
of Lie algebras are (trivially braided) quotients thereof for
by Serre relations: The basis consists of derivational elements (=primitives), the higher powers usually solemnly of higher derivations and there are no further quotients still preserving V ("universal"). In the braided context, the "true" enveloping turns out to be often much smaller:(note that in the further development of the theory, see below, the Nichols algebra takes rather the role of the quantum Borel part of the enveloping!)
-
- There are three equivalent characterizations, as proven by W. Nichols around 1978 (better source ? see discussion) They essentially means, that the "superfluous elements" in the braided Hopf algebra TV are exactly corresponding to "extra-primitives" arrising in higher degree, and are exactly detected by all partial skew-derivations being zero "as if it were a constant".
Definition I: Universal quotient
Let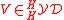. There exists a largest idealIdeal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
of
with the following properties:
-
-
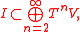
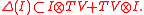One has 
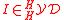, and the quotient 
is a braided Hopf algebra in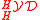 
, the Nichols algebra. It is the "smallest" braided Hopf algebra containing V as a primitive elements (a-priori among others, but see below!)
-
Definition II: Prescribed primitives
There's a unique braided Hopf algebra, generated by V being primitives, which contains no other primitive elements. It is as well the Nichols algebra.Definition III: Skew derivatives
Chosen a homogeneous basis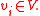 (i.e. coaction/graduation ) one may define skew derivations 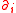, using the universal property of the tensor algebra:
Then the Nichols algebra is the quotient of TV by the largest homogeneous ideal which contains no constants and is invariant under all derivations
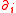.This ideal is larger (and in some cases strictly larger) than the ideal generated by the intersection of
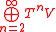with the kernels of the skew derivations 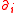.Examples
We give examples of finite dimensional Nichols algebras. Over characteristic p, this effect already may appear in the non-braided situation, namely the truncated universal envelopings of p-restricted Lie algebras. In characteristic zero and with a braiding coming from an abelian group, this seems to be a similarly frequent occurrence (however more involved, see Classification). For G nonabelian on the other side, only very few examples are known so far, and powerful negation criteria exclude many groups at all (see Classification).1-dimensional examples
As a first example, consider the 1-dimensional Yetter–Drinfel'd module over the Group Hopf algebraGroup Hopf algebra
In mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.-Definition:...
with the Cyclic groupCyclic group
In group theory, a cyclic group is a group that can be generated by a single element, in the sense that the group has an element g such that, when written multiplicatively, every element of the group is a power of g .-Definition:A group G is called cyclic if there exists an element g...
multiplicatively denoted (as usual in algebra) and generated by some g.
- Take as H-coaction (resp.
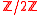-graduation) on 
: 
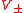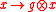
- Take as H-action (resp.
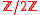-action) on 
: 
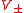- Thus the braiding is
Then, depending on the sign choice, the Nichols algebras are:
Note that the first is as expected (the non-braided case), while the second has been truncated to the point that it's finite dimensional! Similarly,
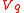over a higher cyclic group with g acting by some 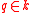has Nichols algebra 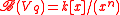if is a primitive n-th root of unity, and otherwise.(from a physical perspective, the
corresponds to a boson, while represents a fermion restricted by Pauli exclusion principlePauli exclusion principle
The Pauli exclusion principle is the quantum mechanical principle that no two identical fermions may occupy the same quantum state simultaneously. A more rigorous statement is that the total wave function for two identical fermions is anti-symmetric with respect to exchange of the particles...
; an analogy that repeats when considering braided commutators, being (anti)commutators in these cases, see also Supersymmetry as a quantum group
Supersymmetry as a quantum group
The concept in theoretical physics of supersymmetry can be reinterpreted in the language of noncommutative geometry and quantum groups. In particular, it involves a mild form of noncommutativity, namely supercommutativity.-F:...
and discussion)
Higher-rank examples over G abelian: braided commutators
The next examples show the interaction of two basis elements: Consider the 2-dimensional Yetter–Drinfel'd module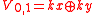 over the group Hopf algebraGroup Hopf algebra
In mathematics, the group Hopf algebra of a given group is a certain construct related to the symmetries of group actions. Deformations of group Hopf algebras are foundational in the theory of quantum groups.-Definition:...
with the Klein four group multiplicatively denoted and generated by some g,h.
- Take as H-coaction/graduation on
: 
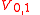and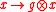 
- Take as H-action (resp.
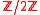-action) on 
:
-
-
-
-
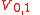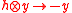
with "+" for 
(symmetric) and "−" for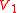 
(assymmetric)
-
- Thus the braiding is
-
Then, depending on the sign choice, the Nichols algebras are of dimension 4 and 8 (they appear in the classification under
):
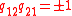There one can see the striking resemblance to Semisimple Lie algebras: In the first case, the braided commutator
Braided vector space
In mathematics, a braided vectorspace \;V is a vectorspace together with an additional structure map \tau\; symbolizing interchanging of two vector tensor copies:such that the Yang–Baxter equation is fulfilled...
[x,y] (here: anticommutator) is zero, while in the second, the root string
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
is longer [x,[x,y]] = 0. Hence these two belong to Dynkin diagrams
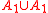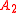and .One also constructs examples with even longer root strings
corresponding to Dynkin diagrams (but as well no higher ones!)Known examples over G nonabelian
Only a handfull of finite dimensional Nichols algebras over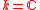 are known so far. It is known that in this case each irreducible Yetter–Drinfel'd module 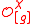corresponds to Conjugacy classConjugacy class
In mathematics, especially group theory, the elements of any group may be partitioned into conjugacy classes; members of the same conjugacy class share many properties, and study of conjugacy classes of non-abelian groups reveals many important features of their structure...
of the group (together with a irreducible representation of the centralizer
Centralizer and normalizer
In group theory, the centralizer and normalizer of a subset S of a group G are subgroups of G which have a restricted action on the elements of S and S as a whole, respectively...
of g). An arbitrary Yetter–Drinfel'd module is a direct sum
Direct sum
In mathematics, one can often define a direct sum of objectsalready known, giving a new one. This is generally the Cartesian product of the underlying sets , together with a suitably defined structure. More abstractly, the direct sum is often, but not always, the coproduct in the category in question...
of such
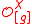, the number of summands is called rank; each summand corresponds to anode in the Dynkin diagram (see below). Note that for the abelian groups as above, the irreducible summands are 1-dimensional, hence rank and dimension coinncide!| Group G | Conjugacy class | Dimension of  | Dimension of 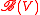 | Source |
|---|---|---|---|---|
| Symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... 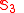 | 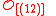 | 3 | 12 | |
| Symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... 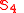 | 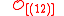 | 6 | 576 | |
| Symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself... 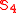 | 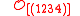 | 6 | 576 | |
| Symmetric group Symmetric group In mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...  | 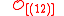 | 10 | 8294400 | |
| Dihedral group Dihedral group In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three... 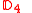 |  | 4 | 64 |
Some more examples are found e.g. in the "zoo" on M. Grana's Webpace page (please add more information, see discussion).
Recently, a family of
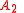example of rank 2 over extensions of has been constructedClassification
the following section could use more details. Please add to it, see discussionOver abelian groups
The Nichols algebras of finite dimension over abelian groups in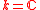 were classified by Istvan Heckenberger in the years 2004–2005 by classifying arithmetic root systemRoot system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
s and generalized Dynkin diagrams; where already Kharchenko had proven them to posess a Poincare–Birkhoff–Witt basis
Poincaré–Birkhoff–Witt theorem
In the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra...
of iterated (braided) commutators. The only information one requires is the braiding matrix, which is diagonal in this setting (see examples above)
While mostly only the classical Cartan-cases appear, there are several exotic diagrams possible for small primes, such as a triangle
In these cases the Weyl reflections
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of one diagram may not land in the "same" diagram, but a so-called Weyl equivalent. This is also the exact reason, that these exotic cases possess a Weyl-groupoid
Groupoid
In mathematics, especially in category theory and homotopy theory, a groupoid generalises the notion of group in several equivalent ways. A groupoid can be seen as a:...
instead of a usual group (picture?).
Negative criteria: abelian subracks
Especially for irreducible V there are no submodules; however one may use the more abstract notion of subrack only reflecting the braiding of two contained elements. In several papers, Nicolas Andruskiewitsch et al. gave negative criteria excluding groups at all from possessing (indecomposable) Nichols algebras. Their techniques can be roughly summarized (more details!):-
- Consider a subrack that is abelian, check which representation my be inherited from the larger rack, and looked up in Heckenbegers List
This ansatz puts sometimes strong conditions especially on the braiding
Yetter-Drinfeld category
In mathematics a Yetter–Drinfel'd category is a special type of braided monoidal category. It consists of modules over a Hopf algebra which satisfy some additional axioms.- Definition :...
of any
-graded element with itself (e.g the first example above shows 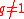). Note that because is central in the centralizer, it acts on the irreducible representation by a scalar as a consequence of the Schur lemma; hence this selfbraiding resp. 1-dim sub-Yetter-Drinfel'd-module / braided vectorspace / 1-dim subrack is diagonal
It is usually used to excludes
e.g. of being of odd order and/or of high dimension:
- If
is real (i.e. conjugated to its inverse) then 
(especially 
has to be of even order) - If
is quasi-real (i.e. conugated to some 
-th power) then
- either
as above - or
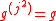and the representation 
is one-dimensional with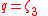 
a primitive 3rd root of unityRoot of unityIn mathematics, a root of unity, or de Moivre number, is any complex number that equals 1 when raised to some integer power n. Roots of unity are used in many branches of mathematics, and are especially important in number theory, the theory of group characters, field theory, and the discrete...
(especially the order of
is divisible by 3)
- either
- If contrary
is an involution and some centralizing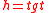 
, then the eigenvalues of the 
(viewed as matrix) acting on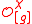 
is strongly restricted.
Root systems over nonabelian groups
On the other hand, Schneider and Heckenberger established the existence an arithmetic root system over nonabelian groups (as in the abelian case), including again a Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
oid and a Poincare–Birkhoff–Witt basis
Poincaré–Birkhoff–Witt theorem
In the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra...
of iterated (braided) commutators
Immediate consequences are implied for rank 2 Nichols algebras
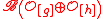which g, h discommuting; then:
- The braided commutators
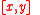of elements 
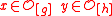are not all zero. - The space of braided commutators
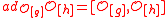form an irreducible sub-Yetter–Drinfel'd module 
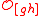(i.e. the root is unique as in the Lie algebra case) - They're "close to commuting"
This implies roughly, that finite dimensional Nichols algebras over nonabelian groups have to be (if at all) of very low rank.
Negative criteria: nonabelian subracks (type D)
As the abelian subracks use the structural classification of Heckenberger for Nichols algebras over abelian groups (see above) one can also consider nonabelian subracks. If such a subrack decomposes into several pieces (because now less element are present to conjugate), then the above results on root systems apply.A specific case where this is highly successful is type D, i.e. for
-
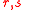not conjugate in the generated subgroup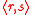 
-
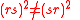
in this case the Nichols algebra of the subrack is infinite dimensional and so is the entire Nichols algebra
Known groups not admitting finite dimensional Nichols algebras
Both negation techniques above have been very fruitful to negate (indecomposable) finite-dimensional Nichols algebras:- for Symmetric groupSymmetric groupIn mathematics, the symmetric group Sn on a finite set of n symbols is the group whose elements are all the permutations of the n symbols, and whose group operation is the composition of such permutations, which are treated as bijective functions from the set of symbols to itself...
s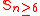
and Alternating groupss 
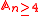(type D) - some group of Lie typeGroup of Lie typeIn mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
(sources, complete list?) - all Sporadic groupSporadic groupIn the mathematical field of group theory, a sporadic group is one of the 26 exceptional groups in the classification of finite simple groups. A simple group is a group G that does not have any normal subgroups except for the subgroup consisting only of the identity element, and G itself...
s except a short list of possibilities (resp. conjugacy classes in ATLAS notation) that are all real or
-quasireal: - ...for the Fisher group
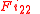the classes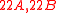 
- ...for the baby monster groupBaby Monster groupIn the mathematical field of group theory, the Baby Monster group B is a group of orderThe Baby Monster group is one of the sporadic groups, and has the second highest order of these, with the highest order being that of the Monster group...
the classes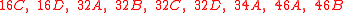 
- ...for the monster groupMonster groupIn the mathematical field of group theory, the Monster group M or F1 is a group of finite order:...
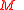the classes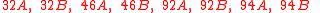 
Usually a large amount of conjugacy classes ae of type D ("not commutative enough"), while the others tend to posess sufficient abelian subracks and can be excluded by their consideration. Several cases have to be done by-hand. Note that the open cases tend to have very small centralizers (usually cyclic) and representations
(usually the 1-dimensional sign representation). Significant exceptions are the conjugacy classes of order 16, 32 having as centralizers p-groupsP-group
In mathematics, given a prime number p, a p-group is a periodic group in which each element has a power of p as its order: each element is of prime power order. That is, for each element g of the group, there exists a nonnegative integer n such that g to the power pn is equal to the identity element...
of order 2048 resp. 128 and currently no restrictions on
Applications
The Nichols algebra appears as quantum Borel part in the classification of finite-dimensional pointed Hopf algebras (without small primes) by Nicolas Andruskiewitsch and Hans-Jürgen Schneider, especially Quantum groupss. For example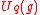 and their well known truncations for q a root of unity decompose just like an ordinary Semisimple Lie algebra into E´s (Borel part), dual F´s and K´s (Cartan algebra):
Here, as in the classical theory V is a vectorspace of dimension n (the rank of
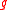) spanned by the E´s, and (a so-called cocylce twist) creates the nontrivial linking between E´s and F´s. Note that in contrast to classical theory, more than two linked components may appear. See cit. loc. for an exotic example with 4 parts of type 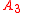.The classification roughly reduces a given hypothetical example to a Radford biproduct
Braided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
of the (coradical-) group and the (connected-) part, which contains the Nichols algebra, by taking the corresponding "graded object" (killing all linkings). With the knowledge from the classification of finite dimensional Nichols algebras above, the authors prove no additional elements to appear in the connected part (generation in degree 1), and finally describe all possible liftings as "dotted lines" in generalized Dynkin diagrams.
Recently, this correspondence has been greatly extended to identify certain so-called coideal subalgebras to be in 1:1 correspondence to the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
, which has been conjectued as "numercal coincidence" earlier and proven in certain cases by-hand.