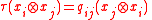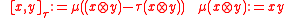Braided vector space
Encyclopedia
In mathematics, a braided vectorspace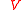 
is a vectorspace together with an additional structure map 
symbolizing interchanging of two vector tensor copies
:
such that the Yang–Baxter equation is fulfilled. Hence drawing tensor diagram
s with
an overcorssing the corresponding composed morphism is unchanged when a Reidemeister move
is applied to the tensor diagram and thus they present a representation of the braid group
.
As first example, every vector space is braided via the trivial braiding (simply flipping). A superspace
has a braiding with negative sign in braiding two odd vectors. More generally, a diagonal braiding means that for a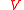
-base 
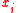we have
A good source for braided vector spaces entire braided monoidal categories with braidings between any objects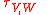
, most importantly the modules over quasitriangular Hopf algebras and Yetter–Drinfel'd modules over finite groups (such as 
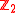above)
If
additionally possesses an algebra structure inside the braided category
("braided algebra") one has a braided commutator (e.g. for a superspace
the anticommutator
):
Examples of such braided algebras (and even Hopf algbebras
) are the Nichols algebras, that are by definition generated by a given braided vectorspace. They appear as quantum Borel part of quantum group
s and oten (eg. when finite or over an abelian group) posess a arithmetic root system
, multiple Dynkin diagrams und a PBW-basis
made up of braided commutators just like the ones in semisimple lie algebras.
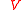is a vectorspace together with an additional structure map symbolizing interchanging of two vector tensor copiesTensor product
In mathematics, the tensor product, denoted by ⊗, may be applied in different contexts to vectors, matrices, tensors, vector spaces, algebras, topological vector spaces, and modules, among many other structures or objects. In each case the significance of the symbol is the same: the most general...
:
such that the Yang–Baxter equation is fulfilled. Hence drawing tensor diagram
Penrose graphical notation
In mathematics and physics, Penrose graphical notation or tensor diagram notation is a visual depiction of multilinear functions or tensors proposed by Roger Penrose. A diagram in the notation consists of several shapes linked together by lines, much like tinker toys...
s with
an overcorssing the corresponding composed morphism is unchanged when a Reidemeister moveReidemeister move
In the mathematical area of knot theory, a Reidemeister move refers to one of three local moves on a link diagram. In 1926, Kurt Reidemeister and independently, in 1927, J.W. Alexander and G.B...
is applied to the tensor diagram and thus they present a representation of the braid group
Braid group
In mathematics, the braid group on n strands, denoted by Bn, is a group which has an intuitive geometrical representation, and in a sense generalizes the symmetric group Sn. Here, n is a natural number; if n > 1, then Bn is an infinite group...
.
As first example, every vector space is braided via the trivial braiding (simply flipping). A superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
has a braiding with negative sign in braiding two odd vectors. More generally, a diagonal braiding means that for a
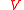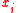-base we have
A good source for braided vector spaces entire braided monoidal categories with braidings between any objects
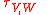, most importantly the modules over quasitriangular Hopf algebras and Yetter–Drinfel'd modules over finite groups (such as 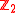above)If
additionally possesses an algebra structure inside the braided categoryBraided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
("braided algebra") one has a braided commutator (e.g. for a superspace
Superspace
"Superspace" has had two meanings in physics. The word was first used by John Wheeler to describe the configuration space of general relativity; for example, this usage may be seen in his famous 1973 textbook Gravitation....
the anticommutator
Commutator
In mathematics, the commutator gives an indication of the extent to which a certain binary operation fails to be commutative. There are different definitions used in group theory and ring theory.-Group theory:...
):
Examples of such braided algebras (and even Hopf algbebras
Braided Hopf algebra
In mathematics a braided Hopf algebra is a Hopf algebra in a braided monoidal category. The most common braided Hopf algebras are objects in a Yetter–Drinfel'd category of a Hopf algebra H, particurlarly the Nichols algebra of a braided vectorspace in that category.The notion should not be confused...
) are the Nichols algebras, that are by definition generated by a given braided vectorspace. They appear as quantum Borel part of quantum group
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
s and oten (eg. when finite or over an abelian group) posess a arithmetic root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, multiple Dynkin diagrams und a PBW-basis
Poincaré–Birkhoff–Witt theorem
In the theory of Lie algebras, the Poincaré–Birkhoff–Witt theorem is a result giving an explicit description of the universal enveloping algebra of a Lie algebra...
made up of braided commutators just like the ones in semisimple lie algebras.