
Brownian Model of Financial Markets
Encyclopedia
The Brownian motion
models for financial markets are based on the work of Robert C. Merton
and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William Sharpe
, and are concerned with defining the concepts of financial assets and markets, portfolios
, gains and wealth
in terms of continuous-time stochastic processes.
Under this model, these assets have continuous prices evolving continuously in time and are driven by Brownian motion processes. This model requires an assumption of perfectly divisible assets and a frictionless market
(i.e. that no transaction costs occur either for buying or selling). Another assumption is that asset prices have no jumps, that is there are no surprises in the market. This last assumption is removed in jump diffusion models.
 financial assets, where one of these assets, called a bond
financial assets, where one of these assets, called a bond
or money-market, is risk
free while the remaining assets, called stocks
assets, called stocks
, are risky.
 :
:
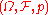 be a probability space
be a probability space
, and a
 be
be
D-dimensional Brownian motion stochastic process
, with the natural filtration:
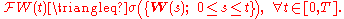
If are the measure 0 (i.e. null under
are the measure 0 (i.e. null under
measure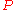 ) subsets of
) subsets of  , then define
, then define
the augmented filtration:
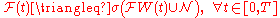
The difference between and
and  is that the
is that the
latter is both left-continuous, in the sense that:
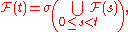
and right-continuous, such that:

while the former is only left-continuous .
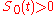 at time
at time
 with
with  , is continuous,
, is continuous,  adapted, and has finite variation
adapted, and has finite variation
. Because it has finite variation, it can be decomposed into an absolutely continuous
part and a singularly continuous part
and a singularly continuous part  , by Lebesgue's decomposition theorem
, by Lebesgue's decomposition theorem
. Define:
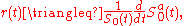 and
and
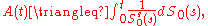
resulting in the SDE
:

which gives:
Thus, it can be easily seen that if is absolutely continuous (i.e.
is absolutely continuous (i.e. 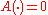 ), then the price of the bond evolves like the value of a risk-free savings account with instantaneous interest rate
), then the price of the bond evolves like the value of a risk-free savings account with instantaneous interest rate 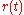 , which is random, time-dependendent and
, which is random, time-dependendent and  measurable.
measurable.
). As a premium for the risk originating from these random fluctuations, the mean rate of return of a stock is higher than that of a bond.
Let be the strictly positive prices per share of the
be the strictly positive prices per share of the  stocks, which are continuous stochastic processes satisfying:
stocks, which are continuous stochastic processes satisfying:

Here,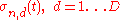 gives the volatility of the
gives the volatility of the  -th stock, while
-th stock, while 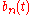 is its mean rate of return.
is its mean rate of return.
In order for an arbitrage
-free pricing scenario,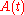 must be as defined above. The solution to this is:
must be as defined above. The solution to this is:

and the discounted stock prices are:
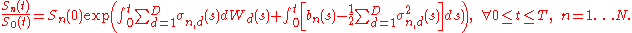
Note that the contribution due to the discontinuites in the bond price does not appear in this equation.
does not appear in this equation.
rate process giving the rate of divident payment per unit price of the stock at time
giving the rate of divident payment per unit price of the stock at time  . Accounting for this in the model, gives the yield process
. Accounting for this in the model, gives the yield process  :
:

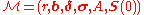 .
.
A portfolio process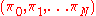 for this market is an
for this market is an 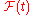 measurable,
measurable, 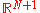 valued process such that:
valued process such that:
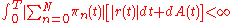 , almost surely
, almost surely
,
 , almost surely, and
, almost surely, and
 , almost surely.
, almost surely.
The gains process for this porfolio is:
We say that the porfolio is self-financed
if:
 .
.
It turns out that for a self-financed portfolio, the appropriate value of is determined from
is determined from 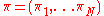 and therefore sometimes
and therefore sometimes  is referred to as the portfolio process. Also,
is referred to as the portfolio process. Also,  implies borrowing money from the money-market, while
implies borrowing money from the money-market, while  implies taking a short position on the stock.
implies taking a short position on the stock.
The term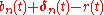 in the SDE of
in the SDE of 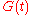 is the risk premium
is the risk premium
process, and it is the compensation received in return for investing in the -th stock.
-th stock.
 , and let
, and let 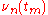 be the number of shares of asset
be the number of shares of asset 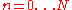 , held in a portfolio during time interval at time
, held in a portfolio during time interval at time  . To avoid the case of insider trading
. To avoid the case of insider trading
(i.e. foreknowledge of the future), it is required that is
is  measurable.
measurable.
Therefore, the incremental gains at each trading interval from such a portfolio is:
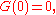
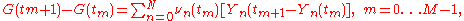
and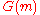 is the total gain over time
is the total gain over time 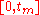 , while the total value of the portfolio is
, while the total value of the portfolio is  .
.
Define , let the time partition go to zero, and substitute for
, let the time partition go to zero, and substitute for 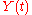 as defined earlier, to get the corresponding SDE for the gains process. Here
as defined earlier, to get the corresponding SDE for the gains process. Here  denotes the dollar amount invested in asset
denotes the dollar amount invested in asset  at time
at time  , not the number of shares held.
, not the number of shares held.
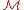 , then a cumulative income process
, then a cumulative income process  is a semimartingale
is a semimartingale
and represents the income accumulated over time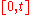 , due to sources other than the investments in the
, due to sources other than the investments in the  assets of the financial market.
assets of the financial market.
A wealth process is then defined as:
is then defined as:

and represents the total wealth of an investor at time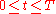 . The portfolio is said to be
. The portfolio is said to be 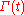 -financed if:
-financed if:

The corresponding SDE for the wealth process, through appropriate substitutions, becomes:
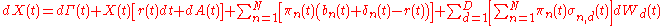 .
.
Note, that again in this case, the value of can be determined from
can be determined from  .
.
. If such opportunities exists, it implies the possibility of making an arbitrarily large risk-free profit.
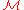 , a self-financed portfolio process
, a self-financed portfolio process  is said to be an arbitrage
is said to be an arbitrage
opportunity if the associated gains process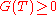 , almost surely and
, almost surely and 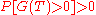 strictly. A market
strictly. A market  in which no such portfolio exists is said to be viable.
in which no such portfolio exists is said to be viable.
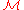 , there exists a
, there exists a 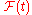 adapted process
adapted process  such that for almost every
such that for almost every 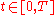 :
:
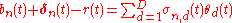 .
.
This is called the market price of risk and relates the premium for the
is called the market price of risk and relates the premium for the  -the stock with its volatility
-the stock with its volatility  .
.
Conversely, if there exists a D-dimensional process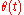 such that it satifies the above requirement, and:
such that it satifies the above requirement, and:

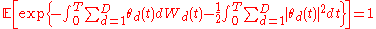 ,
,
then the market is viable.
Also, a viable market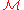 can have only one money-market (bond) and hence only one risk-free rate. Therefore, if the
can have only one money-market (bond) and hence only one risk-free rate. Therefore, if the  -th stock entails no risk (i.e.
-th stock entails no risk (i.e. 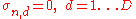 ) and pays no dividend (i.e.
) and pays no dividend (i.e. ), then its rate of return is equal to the money market rate (i.e.
), then its rate of return is equal to the money market rate (i.e.  ) and its price tracks that of the bond (i.e.
) and its price tracks that of the bond (i.e. 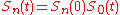 ).
).
 is said to be standard if: It is viable. The number of stocks
is said to be standard if: It is viable. The number of stocks  is not greater than the dimension
is not greater than the dimension  of the underlying Brownian motion process
of the underlying Brownian motion process 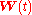 . The market price of risk process
. The market price of risk process 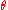 satisfies:
satisfies:
 is greater than the dimension
is greater than the dimension  , in violation of point (ii), from linear algebra, it can be seen that there are
, in violation of point (ii), from linear algebra, it can be seen that there are  stocks whose volatilies (given by the vector
stocks whose volatilies (given by the vector 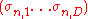 ) are linear combination of the volatilities of
) are linear combination of the volatilities of  other stocks (because the rank of
other stocks (because the rank of  is
is  ). Therefore, the
). Therefore, the  stocks can be replaced by
stocks can be replaced by  equivalent mutual funds.
equivalent mutual funds.
The standard martingale measure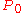 on
on 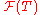 for the standard market, is defined as:
for the standard market, is defined as: .
.
Note that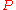 and
and 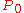 are absolutely continuous with respect to each other, i.e. they are equivalent. Also, according to Girsanov's theorem,
are absolutely continuous with respect to each other, i.e. they are equivalent. Also, according to Girsanov's theorem,
 ,
,
is a -dimensional Brownian motion process on the filtration
-dimensional Brownian motion process on the filtration  with respect to
with respect to 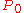 .
.
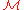 be a standard financial market, and
be a standard financial market, and  be an
be an 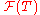 -measurable random variable, such that:
-measurable random variable, such that:
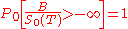 .
.
 ,
,
The market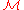 is said to be complete if every such
is said to be complete if every such  is financeable, i.e. if there is an
is financeable, i.e. if there is an  -financed portfolio process
-financed portfolio process 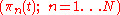 , such that its associated wealth process
, such that its associated wealth process 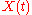 satisfies
satisfies
 , almost surely.
, almost surely.
 at time
at time  , the amount of which is unknown at time
, the amount of which is unknown at time  , then a conservative strategy would be to set aside an amount
, then a conservative strategy would be to set aside an amount 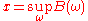 in order to cover the payment. However, in a complete market it is possible to set aside less capital (viz.
in order to cover the payment. However, in a complete market it is possible to set aside less capital (viz.  ) and invest it so that at time
) and invest it so that at time  it has grown to match the size of
it has grown to match the size of  .
.
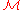 is complete if and only if
is complete if and only if  , and the
, and the 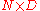 volalatily process
volalatily process  is non-singular for almost every
is non-singular for almost every  , with respect to the Lebesgue measure
, with respect to the Lebesgue measure
.
Brownian motion
Brownian motion or pedesis is the presumably random drifting of particles suspended in a fluid or the mathematical model used to describe such random movements, which is often called a particle theory.The mathematical model of Brownian motion has several real-world applications...
models for financial markets are based on the work of Robert C. Merton
Robert C. Merton
Robert Carhart Merton is an American economist, Nobel laureate in Economics, and professor at the MIT Sloan School of Management.-Biography:...
and Paul A. Samuelson, as extensions to the one-period market models of Harold Markowitz and William Sharpe
William Forsyth Sharpe
William Forsyth Sharpe is the STANCO 25 Professor of Finance, Emeritus at Stanford University's Graduate School of Business and the winner of the 1990 Nobel Memorial Prize in Economic Sciences....
, and are concerned with defining the concepts of financial assets and markets, portfolios
Portfolio (finance)
Portfolio is a financial term denoting a collection of investments held by an investment company, hedge fund, financial institution or individual.-Definition:The term portfolio refers to any collection of financial assets such as stocks, bonds and cash...
, gains and wealth
Wealth
Wealth is the abundance of valuable resources or material possessions. The word wealth is derived from the old English wela, which is from an Indo-European word stem...
in terms of continuous-time stochastic processes.
Under this model, these assets have continuous prices evolving continuously in time and are driven by Brownian motion processes. This model requires an assumption of perfectly divisible assets and a frictionless market
Frictionless market
A Frictionless market is a financial market without transaction costs. Friction is a type of market incompleteness. Every complete market is frictionless, but the converse does not hold. In a frictionless market the solvency cone is the halfspace normal to the unique price vector. The...
(i.e. that no transaction costs occur either for buying or selling). Another assumption is that asset prices have no jumps, that is there are no surprises in the market. This last assumption is removed in jump diffusion models.
Financial market processes
Consider a financial market consisting of financial assets, where one of these assets, called a bond
financial assets, where one of these assets, called a bondBond (finance)
In finance, a bond is a debt security, in which the authorized issuer owes the holders a debt and, depending on the terms of the bond, is obliged to pay interest to use and/or to repay the principal at a later date, termed maturity...
or money-market, is risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
free while the remaining
 assets, called stocks
assets, called stocksStocks
Stocks are devices used in the medieval and colonial American times as a form of physical punishment involving public humiliation. The stocks partially immobilized its victims and they were often exposed in a public place such as the site of a market to the scorn of those who passed by...
, are risky.
Definition
A financial market is defined as :
:
- A probability space

- A time interval
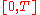
- A
 -dimensional Brownian process
-dimensional Brownian process  adapted to the augmented filtration
adapted to the augmented filtration 
- A measurable risk-free money market rate process

- A measurable mean rate of return process
 .
. - A measurable dividend rate of return process
 .
. - A measurable volatility process
 such that
such that  .
. - A measurable, finite variation, singularly continuous stochastic
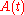
- The initial conditions given by

The augmented filtration
Let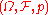 be a probability space
be a probability spaceProbability space
In probability theory, a probability space or a probability triple is a mathematical construct that models a real-world process consisting of states that occur randomly. A probability space is constructed with a specific kind of situation or experiment in mind...
, and a
 be
beD-dimensional Brownian motion stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
, with the natural filtration:
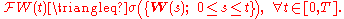
If
 are the measure 0 (i.e. null under
are the measure 0 (i.e. null undermeasure
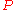 ) subsets of
) subsets of  , then define
, then definethe augmented filtration:
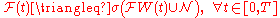
The difference between
 and
and  is that the
is that thelatter is both left-continuous, in the sense that:
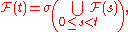
and right-continuous, such that:

while the former is only left-continuous .
Bond
A share of a bond (money market) has price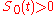 at time
at time with
with  , is continuous,
, is continuous,  adapted, and has finite variation
adapted, and has finite variationBounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
. Because it has finite variation, it can be decomposed into an absolutely continuous
Absolute continuity
In mathematics, the relationship between the two central operations of calculus, differentiation and integration, stated by fundamental theorem of calculus in the framework of Riemann integration, is generalized in several directions, using Lebesgue integration and absolute continuity...
part
 and a singularly continuous part
and a singularly continuous part  , by Lebesgue's decomposition theorem
, by Lebesgue's decomposition theoremLebesgue's decomposition theorem
In mathematics, more precisely in measure theory, Lebesgue's decomposition theorem is a theorem which states that given \mu and \nu two σ-finite signed measures on a measurable space , there exist two σ-finite signed measures \nu_0 and \nu_1 such that:* \nu=\nu_0+\nu_1\, * \nu_0\ll\mu *...
. Define:
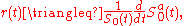 and
and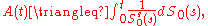
resulting in the SDE
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
:

which gives:

Thus, it can be easily seen that if
 is absolutely continuous (i.e.
is absolutely continuous (i.e. 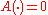 ), then the price of the bond evolves like the value of a risk-free savings account with instantaneous interest rate
), then the price of the bond evolves like the value of a risk-free savings account with instantaneous interest rate 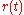 , which is random, time-dependendent and
, which is random, time-dependendent and  measurable.
measurable.Stocks
Stock prices are modeled as being similar to that of bonds, except with a randomly fluctuating component (called its volatilityVolatility (finance)
In finance, volatility is a measure for variation of price of a financial instrument over time. Historic volatility is derived from time series of past market prices...
). As a premium for the risk originating from these random fluctuations, the mean rate of return of a stock is higher than that of a bond.
Let
 be the strictly positive prices per share of the
be the strictly positive prices per share of the  stocks, which are continuous stochastic processes satisfying:
stocks, which are continuous stochastic processes satisfying:
Here,
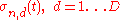 gives the volatility of the
gives the volatility of the  -th stock, while
-th stock, while 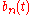 is its mean rate of return.
is its mean rate of return.In order for an arbitrage
Arbitrage
In economics and finance, arbitrage is the practice of taking advantage of a price difference between two or more markets: striking a combination of matching deals that capitalize upon the imbalance, the profit being the difference between the market prices...
-free pricing scenario,
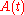 must be as defined above. The solution to this is:
must be as defined above. The solution to this is:
and the discounted stock prices are:
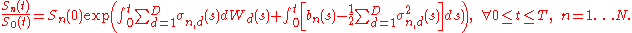
Note that the contribution due to the discontinuites in the bond price
 does not appear in this equation.
does not appear in this equation.Dividend rate
Each stock may have an associated dividendDividend
Dividends are payments made by a corporation to its shareholder members. It is the portion of corporate profits paid out to stockholders. When a corporation earns a profit or surplus, that money can be put to two uses: it can either be re-invested in the business , or it can be distributed to...
rate process
 giving the rate of divident payment per unit price of the stock at time
giving the rate of divident payment per unit price of the stock at time  . Accounting for this in the model, gives the yield process
. Accounting for this in the model, gives the yield process  :
:
Definition
Consider a financial market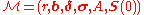 .
.A portfolio process
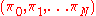 for this market is an
for this market is an 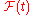 measurable,
measurable, 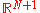 valued process such that:
valued process such that: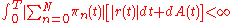 , almost surely
, almost surelyAlmost surely
In probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
,
 , almost surely, and
, almost surely, and , almost surely.
, almost surely.The gains process for this porfolio is:

We say that the porfolio is self-financed
Self-financing portfolio
Self-financing portfolio, an important concept in financial mathematics.A portfolio is self-financing if there is no exogenous infusion or withdrawal of money; the purchase of a new asset must be financed by the sale of an old one.- Mathematical definition :...
if:
 .
.It turns out that for a self-financed portfolio, the appropriate value of
 is determined from
is determined from 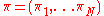 and therefore sometimes
and therefore sometimes  is referred to as the portfolio process. Also,
is referred to as the portfolio process. Also,  implies borrowing money from the money-market, while
implies borrowing money from the money-market, while  implies taking a short position on the stock.
implies taking a short position on the stock.The term
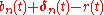 in the SDE of
in the SDE of 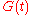 is the risk premium
is the risk premiumRisk premium
A risk premium is the minimum amount of money by which the expected return on a risky asset must exceed the known return on a risk-free asset, in order to induce an individual to hold the risky asset rather than the risk-free asset...
process, and it is the compensation received in return for investing in the
 -th stock.
-th stock.Motivation
Consider time intervals , and let
, and let 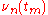 be the number of shares of asset
be the number of shares of asset 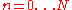 , held in a portfolio during time interval at time
, held in a portfolio during time interval at time  . To avoid the case of insider trading
. To avoid the case of insider tradingInsider trading
Insider trading is the trading of a corporation's stock or other securities by individuals with potential access to non-public information about the company...
(i.e. foreknowledge of the future), it is required that
 is
is  measurable.
measurable.Therefore, the incremental gains at each trading interval from such a portfolio is:
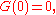
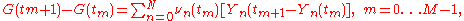
and
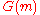 is the total gain over time
is the total gain over time 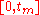 , while the total value of the portfolio is
, while the total value of the portfolio is  .
.Define
 , let the time partition go to zero, and substitute for
, let the time partition go to zero, and substitute for 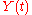 as defined earlier, to get the corresponding SDE for the gains process. Here
as defined earlier, to get the corresponding SDE for the gains process. Here  denotes the dollar amount invested in asset
denotes the dollar amount invested in asset  at time
at time  , not the number of shares held.
, not the number of shares held.Definition
Given a financial market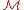 , then a cumulative income process
, then a cumulative income process  is a semimartingale
is a semimartingaleSemimartingale
In probability theory, a real valued process X is called a semimartingale if it can be decomposed as the sum of a local martingale and an adapted finite-variation process....
and represents the income accumulated over time
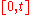 , due to sources other than the investments in the
, due to sources other than the investments in the  assets of the financial market.
assets of the financial market.A wealth process
 is then defined as:
is then defined as:
and represents the total wealth of an investor at time
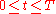 . The portfolio is said to be
. The portfolio is said to be 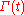 -financed if:
-financed if:
The corresponding SDE for the wealth process, through appropriate substitutions, becomes:
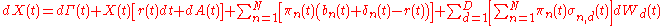 .
.Note, that again in this case, the value of
 can be determined from
can be determined from  .
.Viable markets
The standard theory of mathematical finance is restricted to viable financial markets, i.e. those in which there are no opportunities for arbitrageArbitrage
In economics and finance, arbitrage is the practice of taking advantage of a price difference between two or more markets: striking a combination of matching deals that capitalize upon the imbalance, the profit being the difference between the market prices...
. If such opportunities exists, it implies the possibility of making an arbitrarily large risk-free profit.
Definition
In a financial market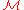 , a self-financed portfolio process
, a self-financed portfolio process  is said to be an arbitrage
is said to be an arbitrageArbitrage
In economics and finance, arbitrage is the practice of taking advantage of a price difference between two or more markets: striking a combination of matching deals that capitalize upon the imbalance, the profit being the difference between the market prices...
opportunity if the associated gains process
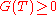 , almost surely and
, almost surely and 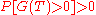 strictly. A market
strictly. A market  in which no such portfolio exists is said to be viable.
in which no such portfolio exists is said to be viable.Implications
In a viable market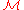 , there exists a
, there exists a 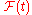 adapted process
adapted process  such that for almost every
such that for almost every 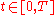 :
: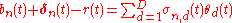 .
.This
 is called the market price of risk and relates the premium for the
is called the market price of risk and relates the premium for the  -the stock with its volatility
-the stock with its volatility  .
.Conversely, if there exists a D-dimensional process
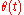 such that it satifies the above requirement, and:
such that it satifies the above requirement, and:
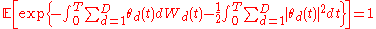 ,
,then the market is viable.
Also, a viable market
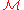 can have only one money-market (bond) and hence only one risk-free rate. Therefore, if the
can have only one money-market (bond) and hence only one risk-free rate. Therefore, if the  -th stock entails no risk (i.e.
-th stock entails no risk (i.e. 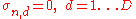 ) and pays no dividend (i.e.
) and pays no dividend (i.e. ), then its rate of return is equal to the money market rate (i.e.
), then its rate of return is equal to the money market rate (i.e.  ) and its price tracks that of the bond (i.e.
) and its price tracks that of the bond (i.e. 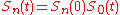 ).
).Definition
A financial market is said to be standard if: It is viable. The number of stocks
is said to be standard if: It is viable. The number of stocks  is not greater than the dimension
is not greater than the dimension  of the underlying Brownian motion process
of the underlying Brownian motion process 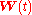 . The market price of risk process
. The market price of risk process 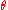 satisfies:
satisfies:
-
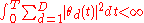 , almost surely. The positive process
, almost surely. The positive process  is a martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
is a martingaleMartingale (probability theory)In probability theory, a martingale is a model of a fair game where no knowledge of past events can help to predict future winnings. In particular, a martingale is a sequence of random variables for which, at a particular time in the realized sequence, the expectation of the next value in the...
.
Comments
In case the number of stocks is greater than the dimension
is greater than the dimension  , in violation of point (ii), from linear algebra, it can be seen that there are
, in violation of point (ii), from linear algebra, it can be seen that there are  stocks whose volatilies (given by the vector
stocks whose volatilies (given by the vector 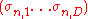 ) are linear combination of the volatilities of
) are linear combination of the volatilities of  other stocks (because the rank of
other stocks (because the rank of  is
is  ). Therefore, the
). Therefore, the  stocks can be replaced by
stocks can be replaced by  equivalent mutual funds.
equivalent mutual funds.The standard martingale measure
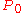 on
on 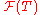 for the standard market, is defined as:
for the standard market, is defined as: .
.Note that
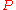 and
and 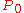 are absolutely continuous with respect to each other, i.e. they are equivalent. Also, according to Girsanov's theorem,
are absolutely continuous with respect to each other, i.e. they are equivalent. Also, according to Girsanov's theorem, ,
,is a
 -dimensional Brownian motion process on the filtration
-dimensional Brownian motion process on the filtration  with respect to
with respect to 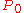 .
.Complete financial markets
A complete financial market is one that allows effective hedging of the risk inherent in any investment strategy.Definition
Let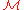 be a standard financial market, and
be a standard financial market, and  be an
be an 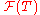 -measurable random variable, such that:
-measurable random variable, such that: .
. ,
,The market
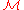 is said to be complete if every such
is said to be complete if every such  is financeable, i.e. if there is an
is financeable, i.e. if there is an  -financed portfolio process
-financed portfolio process 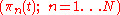 , such that its associated wealth process
, such that its associated wealth process 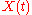 satisfies
satisfies , almost surely.
, almost surely.Motivation
If a particular investment strategy calls for a payment at time
at time  , the amount of which is unknown at time
, the amount of which is unknown at time  , then a conservative strategy would be to set aside an amount
, then a conservative strategy would be to set aside an amount 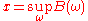 in order to cover the payment. However, in a complete market it is possible to set aside less capital (viz.
in order to cover the payment. However, in a complete market it is possible to set aside less capital (viz.  ) and invest it so that at time
) and invest it so that at time  it has grown to match the size of
it has grown to match the size of  .
.Corollary
A standard financial market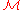 is complete if and only if
is complete if and only if  , and the
, and the 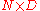 volalatily process
volalatily process  is non-singular for almost every
is non-singular for almost every  , with respect to the Lebesgue measure
, with respect to the Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
See also
- Black-Scholes model
- Martingale pricingMartingale pricingMartingale pricing is a pricing approach based on the notions of martingale and risk neutrality. The martingale pricing approach is a cornerstone of modern quantitative finance and can be applied to a variety of derivatives contracts, e.g...
- Mathematical financeMathematical financeMathematical finance is a field of applied mathematics, concerned with financial markets. The subject has a close relationship with the discipline of financial economics, which is concerned with much of the underlying theory. Generally, mathematical finance will derive and extend the mathematical...
- Monte Carlo methodMonte Carlo methodMonte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...

