
Bruhat–Tits building
Encyclopedia
In mathematics
, a building (also Tits building, Bruhat–Tits building, named after François Bruhat
and Jacques Tits
) is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifold
s, finite projective plane
s, and Riemannian symmetric space
s. Initially introduced by Jacques Tits as a means to understand the structure of exceptional groups of Lie type
, the theory has also been used to study the geometry and topology of homogeneous space
s of p-adic Lie groups and their discrete subgroups of symmetries, in the same way that trees have been used to study free group
s.
as a means of describing simple algebraic groups
over an arbitrary field
. Tits demonstrated how to every such group
G one can associate a simplicial complex
Δ = Δ(G) with an action
of G, called the spherical building of G. The group G imposes very strong combinatorial regularity conditions on the complexes Δ that can arise in this fashion. By treating these conditions as axioms for a class of simplicial complexes, Tits arrived at his first definition of a building. A part of the data defining a building Δ is a Coxeter group
W, which determines a highly symmetrical simplicial complex Σ = Σ(W,S), called the Coxeter complex. A building Δ is glued together from multiple copies of Σ, called its apartments, in a certain regular fashion. When W is a finite Coxeter group, the Coxeter complex is a topological sphere, and the corresponding buildings are said to be of spherical type. When W is an affine Weyl group, the Coxeter complex is a subdivision of the affine plane and one speaks of affine, or Euclidean, buildings. An affine building of type is the same as an infinite tree
is the same as an infinite tree
without terminal vertices.
Although the theory of semisimple algebraic groups provided the initial motivation for the notion of a building, not all buildings arise from a group. In particular, projective planes and generalized quadrangle
s form two classes of graphs studied in incidence geometry which satisfy the axioms of a building, but may not be connected with any group. This phenomenon turns out to be related to the low rank of the corresponding Coxeter system (namely, two). Tits proved a remarkable theorem: all spherical buildings of rank at least three are connected with a group; moreover, if a building of rank at least two is connected with a group then the group is essentially determined by the building.
Iwahori–Matsumoto, Borel–Tits and Bruhat–Tits demonstrated that in analogy with Tits' construction of spherical buildings, affine buildings can also be constructed from certain groups, namely, reductive algebraic groups over a local non-Archimedean field
. Furthermore, if the split rank of the group is at least three, it is essentially determined by its building. Tits later reworked the foundational aspects of the theory of buildings using the notion of a chamber system, encoding the building solely in terms of adjacency properties of simplices of maximal dimension; this leads to simplifications in both spherical and affine cases. He proved that, in analogy with the spherical case, every building of affine type and rank at least four arises from a group.
which is a union of subcomplexes A called apartments such that
An n-simplex in A is called a chamber (originally chambre, i.e. room in French
).
The rank of the building is defined to be n + 1.
W, called the Weyl group
of A, and the simplicial complex A corresponds to the standard geometric realization of W. Standard generators of the Coxeter group are given by the reflections in the walls of a fixed chamber in A. Since
the apartment A is determined up to isomorphism by the building, the same is true of any two simplices in X lie in some common apartment A. When W is finite, the building is said to be spherical. When it is an affine Weyl group, the building is said to be affine or euclidean.
The chamber system is given by the adjacency graph formed by the chambers; each pair of adjacent chambers can in addition be labelled by one of the standard
generators of the Coxeter group (see ).
Every building has a canonical length metric
inherited from the geometric realisation obtained by identifying the vertices with an orthonormal basis
of a Hilbert space
. For affine buildings, this metric satisfies the CAT(0)
comparison inequality of Alexandrov
, known in this setting as the Bruhat-Tits non-positive curvature condition for geodesic triangles: the distance from a vertex to the midpoint of the opposite side is no greater than the distance in the corresponding Euclidean triangle with the same side-lengths (see ).
satisfies the axioms of a BN pair and the Weyl group can identified with N / N B.
B.
Conversely the building can be recovered from the BN pair, so that every BN pair canonically defines a building.
In fact, using the terminology of BN pairs and calling any conjugate of B a Borel subgroup
and any group containing a Borel subgroup a parabolic subgroup,
The same building can often be described by different BN pairs. Moreover not every building comes from a BN pair: this corresponds to the failure of classification results in low rank and dimension (see below).
and geometry
(see ). In this case there are three different buildings, two spherical and one affine. Each is a union of apartments, themselves simplicial complexes. For the affine group, an apartment is just the simplicial complex obtained from the standard tessellation
of Euclidean space En-1 by equilateral (n-1)-simplices; while for a spherical building it is the finite simplicial complex
formed by all (n-1)! simplices with a given common vertex in the analogous tessellation in En-2.
Each building is a simplicial complex X which has to satisfy the following axioms:
and let X be the simplicial complex with vertices the non-trivial vector subspaces of V=Fn. Two subspaces U1 and U2 are connected if one of them is a subset of the other. The k-simplices of X are formed by sets of k + 1
mutually connected subspaces. Maximal connectivity is obtained by taking n - 1 subspaces and the corresponding (n-2)-simplex corresponds to a complete flag
Lower dimensional simplices correspond to partial flags with fewer intermediary subspaces Ui.
To define the apartments in X, it is convenient to define a frame in V as a basis (vi) determined up to scalar multiplication of each of its vectors vi; in other words a frame is a set of one-dimensional subspaces Li = F·vi such that any k of them generate a k-dimensional subspace. Now an ordered frame L1, ..., Ln defines a complete flag via
Since reorderings of the Li's also give a frame, it is straightforward to see that the subspaces, obtained as sums of the Li's,
form a simplicial complex of the type required for an apartment of a spherical building. The axioms for a building can easily be verified using the classical Schreier refinement argument
used to prove the uniqueness of the Jordan-Hölder decomposition.
Qp with respect to the usual non-Archimedean
p-adic norm
||x||p on Q for some prime p. Let R be the subring
of K defined by
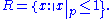
When K = Q, R is the localization
of Z at p and, when K = Qp, R = Zp, the p-adic integers, i.e. the closure of Z in Qp.
The vertices of the building X are the R-lattices in V = Kn, i.e. R-submodules of the form
where (vi) is a basis of V over K. Two lattices are said to be equivalent if one is a scalar multiple of the other by an element of
the multiplicative group K* of K (in fact only integer powers of p need be used). Two lattice L1 and L2 are said to be adjacent if some lattice equivalent to L2 lies between L1 and its sublattice p·L1: this relation is symmetric. The k-simplices of X are equivalence classes of k + 1 mutually adjacent lattices, The (n - 1)- simplices correspond, after relabelling, to chains
where each successive quotient has order p. Apartments are defined by fixing a basis (vi) of V and taking all lattices with basis
(pai vi) where (ai) lies in Zn and is uniquely determined up to addition
of the same integer to each entry.
By definition each apartment has the required form and their union is the whole of X. The second axiom follows by a variant of the Schreier refinement argument. The last
axiom follows by a simple counting argument based on the orders of finite Abelian groups of the form
A standard compactness argument shows that X is in fact independent of the choice of K. In particular taking K = Q, it follows that X is countable. On the other hand taking K = Qp, the definition shows that GLn(Qp) admits a natural simplicial action on the building.
The building comes equipped with a labelling of its vertices with values in Z / n Z. Indeed, fixing a reference lattice L, the label of M is given by
for k sufficiently large. The vertices of any (n – 1)-simplex in X have distinct labels, running through the whole of Z / n Z. Any simplicial automorphism φ of X defines a permutation π of Z / n Z such that label (φ(M)) = π(label (M)). In particular for g in GLn (Qp),
Thus g preserves labels if g lies in SLn(Qp).
of the affine building arises from an element of SLn(Qp). Since automorphisms of the building permute the labels, there is a natural homomorphism
The action of GLn(Qp) gives rise to an n-cycle
τ. Other automorphisms of the building arise from outer automorphisms of SLn(Qp) associated with automorphisms of the Dynkin diagram. Taking the standard
symmetric bilinear form with orthonormal basis vi, the map sending a lattice to its dual lattice gives an automorphism with square the identity, giving the permutation σ that sends each label to its negative modulo n. The image of the above homomorphism is generated by σ and τ and is isomorphic to the dihedral group
Dn of order 2n; when n = 3, it gives the whole of S3.
If E is a finite Galois extension
of Qp and the building is constructed from SLn(E) instead of SLn(Qp), the Galois group
Gal (E/Qp) will also act by automorphisms on the building.
) of rank greater than 2 are associated to simple algebraic or classical groups.
A similar result holds for irreducible affine buildings of dimension greater than two (their buildings "at infinity" are spherical of rank greater than two). In lower rank or dimension, there is no such classification. Indeed each incidence structure
gives a spherical building of rank 2 (see ); and Ballmann and Brin proved that every 2-dimensional simplicial complex in which the links of vertices are isomorphic to the flag complex of a finite projective plane has the structure of a building, not necessarily classical. Many 2-dimensional affine buildings have been constructed using hyperbolic reflection group
s or other more exotic constructions connected with orbifold
s.
Tits also proved that every time a building is described by a BN pair in a group, then in almost all cases the automorphisms of the building correspond to automorphisms of the group (see ).
. The results of Tits on determination of a group by its building have deep connections with rigidity theorems
of George Mostow
and Grigory Margulis
, and with Margulis arithmeticity.
Special types of buildings are studied in discrete mathematics, and the idea of a geometric approach to characterizing simple groups proved very fruitful in the classification of finite simple groups
. The theory of buildings of type more general than spherical or affine is still relatively undeveloped, but these generalized buildings have already found applications to construction of Kac-Moody groups in algebra, and to nonpositively curved manifolds and hyperbolic group
s in topology and geometric group theory
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a building (also Tits building, Bruhat–Tits building, named after François Bruhat
François Bruhat
François Georges René Bruhat was a French mathematician who worked on algebraic groups. The Bruhat order of a Weyl group, the Bruhat decomposition, and the Schwartz–Bruhat functions are named after him....
and Jacques Tits
Jacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
) is a combinatorial and geometric structure which simultaneously generalizes certain aspects of flag manifold
Flag manifold
In mathematics, a generalized flag variety is a homogeneous space whose points are flags in a finite-dimensional vector space V over a field F. When F is the real or complex numbers, a generalized flag variety is a smooth or complex manifold, called a real or complex flag manifold...
s, finite projective plane
Projective plane
In mathematics, a projective plane is a geometric structure that extends the concept of a plane. In the ordinary Euclidean plane, two lines typically intersect in a single point, but there are some pairs of lines that do not intersect...
s, and Riemannian symmetric space
Riemannian symmetric space
In differential geometry, representation theory and harmonic analysis, a symmetric space is a smooth manifold whose group of symmetries contains an inversion symmetry about every point. There are two ways to formulate the inversion symmetry, via Riemannian geometry or via Lie theory...
s. Initially introduced by Jacques Tits as a means to understand the structure of exceptional groups of Lie type
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
, the theory has also been used to study the geometry and topology of homogeneous space
Homogeneous space
In mathematics, particularly in the theories of Lie groups, algebraic groups and topological groups, a homogeneous space for a group G is a non-empty manifold or topological space X on which G acts continuously by symmetry in a transitive way. A special case of this is when the topological group,...
s of p-adic Lie groups and their discrete subgroups of symmetries, in the same way that trees have been used to study free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
s.
Overview
The notion of a building was invented by Jacques TitsJacques Tits
Jacques Tits is a Belgian and French mathematician who works on group theory and geometry and who introduced Tits buildings, the Tits alternative, and the Tits group.- Career :Tits received his doctorate in mathematics at the age of 20...
as a means of describing simple algebraic groups
Group of Lie type
In mathematics, a group of Lie type G is a group of rational points of a reductive linear algebraic group G with values in the field k. Finite groups of Lie type form the bulk of nonabelian finite simple groups...
over an arbitrary field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
. Tits demonstrated how to every such group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G one can associate a simplicial complex
Simplicial complex
In mathematics, a simplicial complex is a topological space of a certain kind, constructed by "gluing together" points, line segments, triangles, and their n-dimensional counterparts...
Δ = Δ(G) with an action
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of G, called the spherical building of G. The group G imposes very strong combinatorial regularity conditions on the complexes Δ that can arise in this fashion. By treating these conditions as axioms for a class of simplicial complexes, Tits arrived at his first definition of a building. A part of the data defining a building Δ is a Coxeter group
Coxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
W, which determines a highly symmetrical simplicial complex Σ = Σ(W,S), called the Coxeter complex. A building Δ is glued together from multiple copies of Σ, called its apartments, in a certain regular fashion. When W is a finite Coxeter group, the Coxeter complex is a topological sphere, and the corresponding buildings are said to be of spherical type. When W is an affine Weyl group, the Coxeter complex is a subdivision of the affine plane and one speaks of affine, or Euclidean, buildings. An affine building of type
 is the same as an infinite tree
is the same as an infinite treeTree (graph theory)
In mathematics, more specifically graph theory, a tree is an undirected graph in which any two vertices are connected by exactly one simple path. In other words, any connected graph without cycles is a tree...
without terminal vertices.
Although the theory of semisimple algebraic groups provided the initial motivation for the notion of a building, not all buildings arise from a group. In particular, projective planes and generalized quadrangle
Generalized quadrangle
A generalized quadrangle is an incidence structure. A generalized quadrangle is by definition a polar space of rank two. They are the generalized n-gons with n=4...
s form two classes of graphs studied in incidence geometry which satisfy the axioms of a building, but may not be connected with any group. This phenomenon turns out to be related to the low rank of the corresponding Coxeter system (namely, two). Tits proved a remarkable theorem: all spherical buildings of rank at least three are connected with a group; moreover, if a building of rank at least two is connected with a group then the group is essentially determined by the building.
Iwahori–Matsumoto, Borel–Tits and Bruhat–Tits demonstrated that in analogy with Tits' construction of spherical buildings, affine buildings can also be constructed from certain groups, namely, reductive algebraic groups over a local non-Archimedean field
Local field
In mathematics, a local field is a special type of field that is a locally compact topological field with respect to a non-discrete topology.Given such a field, an absolute value can be defined on it. There are two basic types of local field: those in which the absolute value is archimedean and...
. Furthermore, if the split rank of the group is at least three, it is essentially determined by its building. Tits later reworked the foundational aspects of the theory of buildings using the notion of a chamber system, encoding the building solely in terms of adjacency properties of simplices of maximal dimension; this leads to simplifications in both spherical and affine cases. He proved that, in analogy with the spherical case, every building of affine type and rank at least four arises from a group.
Definition
An n-dimensional building X is an abstract simplicial complexAbstract simplicial complex
In mathematics, an abstract simplicial complex is a purely combinatorial description of the geometric notion of a simplicial complex, consisting of a family of finite sets closed under the operation of taking subsets...
which is a union of subcomplexes A called apartments such that
- every k-simplex of X is within at least three n-simplices if k < n;
- any (n – 1 )-simplex in an apartment A lies in exactly two adjacent n-simplices of A and the graphGraph theoryIn mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
of adjacent n-simplices is connected; - any two simplices in X lie in some common apartment A;
- if two simplices both lie in apartments A and A ', then there is a simplicial isomorphism of A onto A ' fixing the vertices of the two simplices.
An n-simplex in A is called a chamber (originally chambre, i.e. room in French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
).
The rank of the building is defined to be n + 1.
Elementary properties
Every apartment A in a building is a Coxeter complex. In fact, for every two n-simplices intersecting in an (n – 1)-simplex or panel, there is a unique period two simplicial automorphism of A, called a reflection, carrying one n-simplex onto the other and fixing their common points. These reflections generate a Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
W, called the Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
of A, and the simplicial complex A corresponds to the standard geometric realization of W. Standard generators of the Coxeter group are given by the reflections in the walls of a fixed chamber in A. Since
the apartment A is determined up to isomorphism by the building, the same is true of any two simplices in X lie in some common apartment A. When W is finite, the building is said to be spherical. When it is an affine Weyl group, the building is said to be affine or euclidean.
The chamber system is given by the adjacency graph formed by the chambers; each pair of adjacent chambers can in addition be labelled by one of the standard
generators of the Coxeter group (see ).
Every building has a canonical length metric
Intrinsic metric
In the mathematical study of metric spaces, one can consider the arclength of paths in the space. If two points are a given distance from each other, it is natural to expect that one should be able to get from one point to another along a path whose arclength is equal to that distance...
inherited from the geometric realisation obtained by identifying the vertices with an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
. For affine buildings, this metric satisfies the CAT(0)
CAT(k) space
In mathematics, a CAT space is a specific type of metric space. Intuitively, triangles in a CAT space are "slimmer" than corresponding "model triangles" in a standard space of constant curvature k. In a CAT space, the curvature is bounded from above by k...
comparison inequality of Alexandrov
Aleksandr Danilovich Aleksandrov
Aleksandr Danilovich Aleksandrov , and Alexandrov ) , was a Soviet/Russian mathematician, physicist, philosopher and mountaineer.- Scientific career :...
, known in this setting as the Bruhat-Tits non-positive curvature condition for geodesic triangles: the distance from a vertex to the midpoint of the opposite side is no greater than the distance in the corresponding Euclidean triangle with the same side-lengths (see ).
Connection with BN pairs
If a group G acts simplicially on a building X, transitively on pairs of chambers C and apartments A containing them, then the stabilisers of such a pair define a BN pair or Tits system. In fact the pair of subgroups- B = GC and N = GA
satisfies the axioms of a BN pair and the Weyl group can identified with N / N
 B.
B.Conversely the building can be recovered from the BN pair, so that every BN pair canonically defines a building.
In fact, using the terminology of BN pairs and calling any conjugate of B a Borel subgroup
Borel subgroup
In the theory of algebraic groups, a Borel subgroup of an algebraic group G is a maximal Zariski closed and connected solvable algebraic subgroup.For example, in the group GLn ,...
and any group containing a Borel subgroup a parabolic subgroup,
- the vertices of the building X correspond to maximal parabolic subgroups;
- k + 1 vertices form a k-simplex whenever the intersection of the corresponding maximal parabolic subgroups is also parabolic;
- apartments are conjugates under G of the simplicial subcomplex with vertices given by conjugates under N of maximal parabolics containing B.
The same building can often be described by different BN pairs. Moreover not every building comes from a BN pair: this corresponds to the failure of classification results in low rank and dimension (see below).
Spherical and affine buildings for SLn
The simplicial structure of the affine and spherical buildings associated to SLn(Qp), as well as their interconnections, are easy to explain directly using only concepts from elementary algebraAlgebra
Algebra is the branch of mathematics concerning the study of the rules of operations and relations, and the constructions and concepts arising from them, including terms, polynomials, equations and algebraic structures...
and geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
(see ). In this case there are three different buildings, two spherical and one affine. Each is a union of apartments, themselves simplicial complexes. For the affine group, an apartment is just the simplicial complex obtained from the standard tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of Euclidean space En-1 by equilateral (n-1)-simplices; while for a spherical building it is the finite simplicial complex
formed by all (n-1)! simplices with a given common vertex in the analogous tessellation in En-2.
Each building is a simplicial complex X which has to satisfy the following axioms:
- X is a union of apartments.
- Any two simplices in X are contained in a common apartment.
- If a simplex is contained in two apartments, there is a simplicial isomorphism of one onto the other fixing all common points.
Spherical building
Let F be a fieldField (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
and let X be the simplicial complex with vertices the non-trivial vector subspaces of V=Fn. Two subspaces U1 and U2 are connected if one of them is a subset of the other. The k-simplices of X are formed by sets of k + 1
mutually connected subspaces. Maximal connectivity is obtained by taking n - 1 subspaces and the corresponding (n-2)-simplex corresponds to a complete flag
- (0)
 U1
U1  ···
···  Un – 1
Un – 1  V
V
Lower dimensional simplices correspond to partial flags with fewer intermediary subspaces Ui.
To define the apartments in X, it is convenient to define a frame in V as a basis (vi) determined up to scalar multiplication of each of its vectors vi; in other words a frame is a set of one-dimensional subspaces Li = F·vi such that any k of them generate a k-dimensional subspace. Now an ordered frame L1, ..., Ln defines a complete flag via
- Ui = L1
 ···
···  Li
Li
Since reorderings of the Li's also give a frame, it is straightforward to see that the subspaces, obtained as sums of the Li's,
form a simplicial complex of the type required for an apartment of a spherical building. The axioms for a building can easily be verified using the classical Schreier refinement argument
Schreier refinement theorem
In mathematics, the Schreier refinement theorem of group theory states that any two normal series of subgroups of a given group have equivalent refinements....
used to prove the uniqueness of the Jordan-Hölder decomposition.
Affine building
Let K be a field lying between Q and its p-adic completionP-adic number
In mathematics, and chiefly number theory, the p-adic number system for any prime number p extends the ordinary arithmetic of the rational numbers in a way different from the extension of the rational number system to the real and complex number systems...
Qp with respect to the usual non-Archimedean
Archimedean property
In abstract algebra and analysis, the Archimedean property, named after the ancient Greek mathematician Archimedes of Syracuse, is a property held by some ordered or normed groups, fields, and other algebraic structures. Roughly speaking, it is the property of having no infinitely large or...
p-adic norm
||x||p on Q for some prime p. Let R be the subring
Subring
In mathematics, a subring of R is a subset of a ring, is itself a ring with the restrictions of the binary operations of addition and multiplication of R, and which contains the multiplicative identity of R...
of K defined by
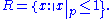
When K = Q, R is the localization
Localization of a ring
In abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
of Z at p and, when K = Qp, R = Zp, the p-adic integers, i.e. the closure of Z in Qp.
The vertices of the building X are the R-lattices in V = Kn, i.e. R-submodules of the form
- L = R·v1
 ···
··· R·vn
R·vn
where (vi) is a basis of V over K. Two lattices are said to be equivalent if one is a scalar multiple of the other by an element of
the multiplicative group K* of K (in fact only integer powers of p need be used). Two lattice L1 and L2 are said to be adjacent if some lattice equivalent to L2 lies between L1 and its sublattice p·L1: this relation is symmetric. The k-simplices of X are equivalence classes of k + 1 mutually adjacent lattices, The (n - 1)- simplices correspond, after relabelling, to chains
- p·Ln
 L1
L1  L2
L2  ···
···  Ln – 1
Ln – 1  Ln
Ln
where each successive quotient has order p. Apartments are defined by fixing a basis (vi) of V and taking all lattices with basis
(pai vi) where (ai) lies in Zn and is uniquely determined up to addition
of the same integer to each entry.
By definition each apartment has the required form and their union is the whole of X. The second axiom follows by a variant of the Schreier refinement argument. The last
axiom follows by a simple counting argument based on the orders of finite Abelian groups of the form
- L + pk ·Li / pk ·Li .
A standard compactness argument shows that X is in fact independent of the choice of K. In particular taking K = Q, it follows that X is countable. On the other hand taking K = Qp, the definition shows that GLn(Qp) admits a natural simplicial action on the building.
The building comes equipped with a labelling of its vertices with values in Z / n Z. Indeed, fixing a reference lattice L, the label of M is given by
- label (M) = logp |M/ pk L| modulo n
for k sufficiently large. The vertices of any (n – 1)-simplex in X have distinct labels, running through the whole of Z / n Z. Any simplicial automorphism φ of X defines a permutation π of Z / n Z such that label (φ(M)) = π(label (M)). In particular for g in GLn (Qp),
- label (g·M) = label (M) + logp || det g ||p modulo n.
Thus g preserves labels if g lies in SLn(Qp).
Automorphisms
Tits proved that any label-preserving automorphismAutomorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
of the affine building arises from an element of SLn(Qp). Since automorphisms of the building permute the labels, there is a natural homomorphism
- Aut X
 Sn.
Sn.
The action of GLn(Qp) gives rise to an n-cycle
Cycle (mathematics)
In mathematics, and in particular in group theory, a cycle is a permutation of the elements of some set X which maps the elements of some subset S to each other in a cyclic fashion, while fixing all other elements...
τ. Other automorphisms of the building arise from outer automorphisms of SLn(Qp) associated with automorphisms of the Dynkin diagram. Taking the standard
symmetric bilinear form with orthonormal basis vi, the map sending a lattice to its dual lattice gives an automorphism with square the identity, giving the permutation σ that sends each label to its negative modulo n. The image of the above homomorphism is generated by σ and τ and is isomorphic to the dihedral group
Dihedral group
In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...
Dn of order 2n; when n = 3, it gives the whole of S3.
If E is a finite Galois extension
Galois extension
In mathematics, a Galois extension is an algebraic field extension E/F satisfying certain conditions ; one also says that the extension is Galois. The significance of being a Galois extension is that the extension has a Galois group and obeys the fundamental theorem of Galois theory.The definition...
of Qp and the building is constructed from SLn(E) instead of SLn(Qp), the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
Gal (E/Qp) will also act by automorphisms on the building.
Geometric relations
Spherical buildings arise in two quite different ways in connection with the affine building X for SLn(Qp):- The link of each vertex L in the affine building corresponds to submodules of L/p·L under the finite field F = R/p·R = Z/(p). This is just the spherical building for SLn(F).
- The building X can be compactifiedCompactification (mathematics)In mathematics, compactification is the process or result of making a topological space compact. The methods of compactification are various, but each is a way of controlling points from "going off to infinity" by in some way adding "points at infinity" or preventing such an "escape".-An...
by adding the spherical building for SLn(Qp) as boundary "at infinity" (see or ).
Classification
Tits proved that all irreducible spherical buildings (i.e. with finite Weyl groupWeyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
) of rank greater than 2 are associated to simple algebraic or classical groups.
A similar result holds for irreducible affine buildings of dimension greater than two (their buildings "at infinity" are spherical of rank greater than two). In lower rank or dimension, there is no such classification. Indeed each incidence structure
Incidence structure
In mathematics, an incidence structure is a tripleC=.\,where P is a set of "points", L is a set of "lines" and I \subseteq P \times L is the incidence relation. The elements of I are called flags. If \in I,...
gives a spherical building of rank 2 (see ); and Ballmann and Brin proved that every 2-dimensional simplicial complex in which the links of vertices are isomorphic to the flag complex of a finite projective plane has the structure of a building, not necessarily classical. Many 2-dimensional affine buildings have been constructed using hyperbolic reflection group
Reflection group
In group theory and geometry, a reflection group is a discrete group which is generated by a set of reflections of a finite-dimensional Euclidean space. The symmetry group of a regular polytope or of a tiling of the Euclidean space by congruent copies of a regular polytope is necessarily a...
s or other more exotic constructions connected with orbifold
Orbifold
In the mathematical disciplines of topology, geometry, and geometric group theory, an orbifold is a generalization of a manifold...
s.
Tits also proved that every time a building is described by a BN pair in a group, then in almost all cases the automorphisms of the building correspond to automorphisms of the group (see ).
Applications
The theory of buildings has important applications in several rather disparate fields. Besides the already mentioned connections with the structure of reductive algebraic groups over general and local fields, buildings are used to study their representationsGroup representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
. The results of Tits on determination of a group by its building have deep connections with rigidity theorems
Mostow rigidity theorem
In mathematics, Mostow's rigidity theorem, or strong rigidity theorem, or Mostow–Prasad rigidity theorem, essentially states that the geometry of a finite-volume hyperbolic manifold of dimension greater than two is determined by the fundamental group and hence unique...
of George Mostow
George Mostow
George Mostow is an American mathematician, a member of the National Academy of Sciences, Henry Ford II Professor of Mathematics at Yale University, the 49th President of the American Mathematical Society ,...
and Grigory Margulis
Grigory Margulis
Gregori Aleksandrovich Margulis is a Russian mathematician known for his far-reaching work on lattices in Lie groups, and the introduction of methods from ergodic theory into diophantine approximation. He was awarded a Fields Medal in 1978 and a Wolf Prize in Mathematics in 2005, becoming the...
, and with Margulis arithmeticity.
Special types of buildings are studied in discrete mathematics, and the idea of a geometric approach to characterizing simple groups proved very fruitful in the classification of finite simple groups
Classification of finite simple groups
In mathematics, the classification of the finite simple groups is a theorem stating that every finite simple group belongs to one of four categories described below. These groups can be seen as the basic building blocks of all finite groups, in much the same way as the prime numbers are the basic...
. The theory of buildings of type more general than spherical or affine is still relatively undeveloped, but these generalized buildings have already found applications to construction of Kac-Moody groups in algebra, and to nonpositively curved manifolds and hyperbolic group
Hyperbolic group
In group theory, a hyperbolic group, also known as a word hyperbolic group, Gromov hyperbolic group, negatively curved group is a finitely generated group equipped with a word metric satisfying certain properties characteristic of hyperbolic geometry. The notion of a hyperbolic group was introduced...
s in topology and geometric group theory
Geometric group theory
Geometric group theory is an area in mathematics devoted to the study of finitely generated groups via exploring the connections between algebraic properties of such groups and topological and geometric properties of spaces on which these groups act .Another important...
.

