Brumer–Stark conjecture
Encyclopedia
The Brumer–Stark conjecture is a conjecture
in algebraic number theory
giving a rough generalization of both the analytic class number formula for Dedekind zeta function
s, and also of Stickelberger's theorem
about the factorization
of Gauss sums. It is named after Armand Brumer and Harold Stark
.
It arises as a special case (abelian and first-order) of Stark's conjecture
, when the place that splits completely in the extension is finite. There are very few cases where the conjecture is known to be valid. Its importance arises, for instance, from its connection with Hilbert's twelfth problem
.
of global field
s, and let S be a set of places of k containing the Archimedean places and the prime ideal
s that ramify in K/k. The S-imprimitive equivariant Artin L-function
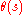is obtained from the usual equivariant Artin L-function by removing the Euler factors corresponding to the primes in S from the Artin L-function
s from which the equivariant function is built. It is a function on the complex number
s taking values in the complex group ring
where G is the Galois group
of K/k. It is analytic on the entire plane, excepting a lone simple pole at s = 1.
Let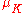
be the group of roots of unity in K. The group G acts on 
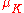; let A be the annihilator
of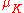
as a 
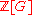-module
. An important theorem, first proved by C. L. Siegel and later independently by Takuro Shintani
, states that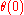
is actually in 
. A deeper theorem, proved independently by Pierre Deligne
and Ken Ribet, Daniel Barsky, and Pierette Cassou-Nogues, states that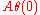
is in 
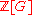. In particular, 
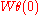is in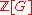 
, where 
is the cardinality of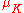
.
The ideal class group
of K is a G-module
. From the above discussion, we can let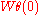
act on it. The Brumer–Stark conjecture says the following:
Brumer–Stark conjecture:
For each nonzero fractional ideal
of K, there is an anti-unit 
such that
The first part of this conjecture is due to Armand Brumer, and Harold Stark originally suggested that the second condition might hold. The conjecture was first stated in published form by John Tate
.
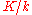where
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
in algebraic number theory
Algebraic number theory
Algebraic number theory is a major branch of number theory which studies algebraic structures related to algebraic integers. This is generally accomplished by considering a ring of algebraic integers O in an algebraic number field K/Q, and studying their algebraic properties such as factorization,...
giving a rough generalization of both the analytic class number formula for Dedekind zeta function
Dedekind zeta function
In mathematics, the Dedekind zeta function of an algebraic number field K, generally denoted ζK, is a generalization of the Riemann zeta function—which is obtained by specializing to the case where K is the rational numbers Q...
s, and also of Stickelberger's theorem
Stickelberger's theorem
In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields...
about the factorization
Factorization
In mathematics, factorization or factoring is the decomposition of an object into a product of other objects, or factors, which when multiplied together give the original...
of Gauss sums. It is named after Armand Brumer and Harold Stark
Harold Stark
Harold Mead Stark is an American mathematician, specializing in number theory. He is best known for his solution of the Gauss class number 1 problem, in effect correcting and completing the earlier work of Kurt Heegner; and for Stark's conjecture. He has recently collaborated with Audrey Terras on...
.
It arises as a special case (abelian and first-order) of Stark's conjecture
Stark's conjecture
In number theory, the Stark conjectures, the first of which were introduced in a series of papers in the 1970s by American mathematician Harold Stark and later greatly expanded by John Tate, give conjectural information about the coefficient of the leading term in the Taylor expansion of an Artin...
, when the place that splits completely in the extension is finite. There are very few cases where the conjecture is known to be valid. Its importance arises, for instance, from its connection with Hilbert's twelfth problem
Hilbert's twelfth problem
Kronecker's Jugendtraum or Hilbert's twelfth problem, of the 23 mathematical Hilbert problems, is the extension of Kronecker–Weber theorem on abelian extensions of the rational numbers, to any base number field...
.
Statement of the conjecture
Let K/k be an abelian extensionAbelian extension
In abstract algebra, an abelian extension is a Galois extension whose Galois group is abelian. When the Galois group is a cyclic group, we have a cyclic extension. More generally, a Galois extension is called solvable if its Galois group is solvable....
of global field
Global field
In mathematics, the term global field refers to either of the following:*an algebraic number field, i.e., a finite extension of Q, or*a global function field, i.e., the function field of an algebraic curve over a finite field, equivalently, a finite extension of Fq, the field of rational functions...
s, and let S be a set of places of k containing the Archimedean places and the prime ideal
Prime ideal
In algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s that ramify in K/k. The S-imprimitive equivariant Artin L-function
Equivariant L-function
In algebraic number theory, an equivariant Artin L-function is a function associated to a finite Galois extension of global fields created by packaging together the various Artin L-functions associated with the extension. Each extension has many traditional Artin L-functions associated with it,...
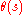is obtained from the usual equivariant Artin L-function by removing the Euler factors corresponding to the primes in S from the Artin L-functionArtin L-function
In mathematics, an Artin L-function is a type of Dirichlet series associated to a linear representation ρ of a Galois group G. These functions were introduced in the 1923 by Emil Artin, in connection with his research into class field theory. Their fundamental properties, in particular the Artin...
s from which the equivariant function is built. It is a function on the complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s taking values in the complex group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
where G is the Galois group
Galois group
In mathematics, more specifically in the area of modern algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension...
of K/k. It is analytic on the entire plane, excepting a lone simple pole at s = 1.
Let
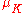be the group of roots of unity in K. The group G acts on 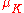; let A be the annihilatorAnnihilator (ring theory)
In mathematics, specifically module theory, annihilators are a concept that generalizes torsion and orthogonal complement.-Definitions:Let R be a ring, and let M be a left R-module. Choose a nonempty subset S of M...
of
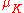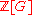as a -moduleModule (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
. An important theorem, first proved by C. L. Siegel and later independently by Takuro Shintani
Takuro Shintani
was a Japanese mathematician working in number theory who introduced Shintani zeta functions.-References:...
, states that
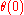is actually in . A deeper theorem, proved independently by Pierre DelignePierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
and Ken Ribet, Daniel Barsky, and Pierette Cassou-Nogues, states that
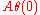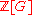is in . In particular, 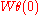is in 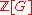, where is the cardinality of
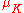.The ideal class group
Ideal class group
In mathematics, the extent to which unique factorization fails in the ring of integers of an algebraic number field can be described by a certain group known as an ideal class group...
of K is a G-module
G-module
In mathematics, given a group G, a G-module is an abelian group M on which G acts compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G...
. From the above discussion, we can let
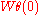act on it. The Brumer–Stark conjecture says the following:Brumer–Stark conjecture:
For each nonzero fractional ideal
Fractional ideal
In mathematics, in particular commutative algebra, the concept of fractional ideal is introduced in the context of integral domains and is particularly fruitful in the study of Dedekind domains. In some sense, fractional ideals of an integral domain are like ideals where denominators are allowed...
of K, there is an anti-unit such that
- The extension
is abelian.
The first part of this conjecture is due to Armand Brumer, and Harold Stark originally suggested that the second condition might hold. The conjecture was first stated in published form by John Tate
John Tate
John Torrence Tate Jr. is an American mathematician, distinguished for many fundamental contributions in algebraic number theory, arithmetic geometry and related areas in algebraic geometry.-Biography:...
.
Progress
The Brumer Stark conjecture is known to be true for extensions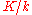 where- k is abelian over
-
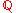
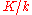is a quadratic extension - K/k is a biquadratic extension