
G-module
Encyclopedia
In mathematics
, given a group
G, a G-module is an abelian group
M on which G acts
compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G
. Group (co)homology
provides an important set of tools for studying general G-modules.
The term G-module is also used for the more general notion of an R-module
on which G acts linearly (i.e. as a group of R-module automorphism
s).
ρ : G×M → M such that
(where g·a denotes ρ(g,a)). A right G-module is defined similarly. Given a left G-module M, it can be turned into a right G-module by defining a·g = g−1·a.
A function
f : M → N is called a morphism of G-modules (or a G-linear map, or a G-homomorphism) if f is both a group homomorphism
and G-equivariant
.
The collection of left (respectively right) G-modules and their morphisms form an abelian category
G-Mod (resp. Mod-G). The category G-Mod (resp. Mod-G) can be identified with the category of left (resp. right) modules
over the group ring
Z[G].
A submodule of a G-module M is a subgroup A ⊆ M that is stable under the action of G, i.e. g·a ∈ A for all g ∈ G and a ∈ A. Given a submodule A of M, the quotient module M/A is the quotient group
with action g·(m + A) = g·m + A.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, given a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G, a G-module is an abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
M on which G acts
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
compatibly with the abelian group structure on M. This widely applicable notion generalizes that of a representation of G
Group representation
In the mathematical field of representation theory, group representations describe abstract groups in terms of linear transformations of vector spaces; in particular, they can be used to represent group elements as matrices so that the group operation can be represented by matrix multiplication...
. Group (co)homology
Group cohomology
In abstract algebra, homological algebra, algebraic topology and algebraic number theory, as well as in applications to group theory proper, group cohomology is a way to study groups using a sequence of functors H n. The study of fixed points of groups acting on modules and quotient modules...
provides an important set of tools for studying general G-modules.
The term G-module is also used for the more general notion of an R-module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
on which G acts linearly (i.e. as a group of R-module automorphism
Automorphism
In mathematics, an automorphism is an isomorphism from a mathematical object to itself. It is, in some sense, a symmetry of the object, and a way of mapping the object to itself while preserving all of its structure. The set of all automorphisms of an object forms a group, called the automorphism...
s).
Definition and basics
Let G be a group. A left G-module consists of an abelian group M together with a left group actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
ρ : G×M → M such that
- g·(a + b) = g·a + g·b
(where g·a denotes ρ(g,a)). A right G-module is defined similarly. Given a left G-module M, it can be turned into a right G-module by defining a·g = g−1·a.
A function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
f : M → N is called a morphism of G-modules (or a G-linear map, or a G-homomorphism) if f is both a group homomorphism
Group homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
and G-equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
.
The collection of left (respectively right) G-modules and their morphisms form an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
G-Mod (resp. Mod-G). The category G-Mod (resp. Mod-G) can be identified with the category of left (resp. right) modules
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
over the group ring
Group ring
In algebra, a group ring is a free module and at the same time a ring, constructed in a natural way from any given ring and any given group. As a free module, its ring of scalars is the given ring and its basis is one-to-one with the given group. As a ring, its addition law is that of the free...
Z[G].
A submodule of a G-module M is a subgroup A ⊆ M that is stable under the action of G, i.e. g·a ∈ A for all g ∈ G and a ∈ A. Given a submodule A of M, the quotient module M/A is the quotient group
Quotient group
In mathematics, specifically group theory, a quotient group is a group obtained by identifying together elements of a larger group using an equivalence relation...
with action g·(m + A) = g·m + A.
Examples
- Given a group G, the abelian group Z is a G-module with the trivial action g·a = a.
- Let M be the set of binary quadratic formBinary quadratic formIn mathematics, a binary quadratic form is a quadratic form in two variables. More concretely, it is a homogeneous polynomial of degree 2 in two variableswhere a, b, c are the coefficients...
s f(x, y) = ax2 + 2bxy + cy2 with a, b, c integerIntegerThe integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
s and let G = SL(2, Z) (the two-by-two special linear groupSpecial linear groupIn mathematics, the special linear group of degree n over a field F is the set of n×n matrices with determinant 1, with the group operations of ordinary matrix multiplication and matrix inversion....
over Z). Define
-
- where
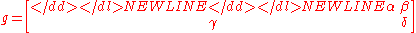
- and (x, y)g is matrix multiplicationMatrix multiplicationIn mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
. Then M is a G-module studied by GaussGaussGauss may refer to:*Carl Friedrich Gauss, German mathematician and physicist*Gauss , a unit of magnetic flux density or magnetic induction*GAUSS , a software package*Gauss , a crater on the moon...
.
- If V is a representation of G over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K, then V is a G-module (it is an abelian group under addition).
Topological groups
If G is a topological groupTopological groupIn mathematics, a topological group is a group G together with a topology on G such that the group's binary operation and the group's inverse function are continuous functions with respect to the topology. A topological group is a mathematical object with both an algebraic structure and a...
and M is an abelian topological group, then a topological G-module is a G-module where the action map G×M → M is continuousContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
(where the product topologyProduct topologyIn topology and related areas of mathematics, a product space is the cartesian product of a family of topological spaces equipped with a natural topology called the product topology...
is taken on G×M).- and (x, y)g is matrix multiplication


