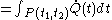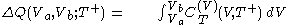Calorimetry
Encyclopedia
Science
Science is a systematic enterprise that builds and organizes knowledge in the form of testable explanations and predictions about the universe...
of measuring the heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
of chemical reaction
Chemical reaction
A chemical reaction is a process that leads to the transformation of one set of chemical substances to another. Chemical reactions can be either spontaneous, requiring no input of energy, or non-spontaneous, typically following the input of some type of energy, such as heat, light or electricity...
s or physical change
Physical change
Physical changes are changes affecting the form of a chemical substance, but do not change the chemical composition of that substance. Physical changes are used to separate mixtures into their component compounds, but can not usually be used to separate compounds into chemical elements or simpler...
s. Calorimetry is performed with a calorimeter
Calorimeter
A calorimeter is a device used for calorimetry, the science of measuring the heat of chemical reactions or physical changes as well as heat capacity. Differential scanning calorimeters, isothermal microcalorimeters, titration calorimeters and accelerated rate calorimeters are among the most common...
. The word calorimetry is derived from the Latin word calor, meaning heat. Scottish physician and scientist Joseph Black
Joseph Black
Joseph Black FRSE FRCPE FPSG was a Scottish physician and chemist, known for his discoveries of latent heat, specific heat, and carbon dioxide. He was professor of Medicine at University of Glasgow . James Watt, who was appointed as philosophical instrument maker at the same university...
, who was the first to recognize the distinction between heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
and temperature
Temperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
, is said to be the founder of calorimetry.
Indirect calorimetry calculates heat
Heat
In physics and thermodynamics, heat is energy transferred from one body, region, or thermodynamic system to another due to thermal contact or thermal radiation when the systems are at different temperatures. It is often described as one of the fundamental processes of energy transfer between...
that living organisms produce from their production of carbon dioxide
Carbon dioxide
Carbon dioxide is a naturally occurring chemical compound composed of two oxygen atoms covalently bonded to a single carbon atom...
and nitrogen waste (frequently ammonia
Ammonia
Ammonia is a compound of nitrogen and hydrogen with the formula . It is a colourless gas with a characteristic pungent odour. Ammonia contributes significantly to the nutritional needs of terrestrial organisms by serving as a precursor to food and fertilizers. Ammonia, either directly or...
in aquatic organisms, or urea
Urea
Urea or carbamide is an organic compound with the chemical formula CO2. The molecule has two —NH2 groups joined by a carbonyl functional group....
in terrestrial ones), OR from their consumption of oxygen
Oxygen
Oxygen is the element with atomic number 8 and represented by the symbol O. Its name derives from the Greek roots ὀξύς and -γενής , because at the time of naming, it was mistakenly thought that all acids required oxygen in their composition...
.
Lavoisier noted in 1780 that heat production can be predicted from oxygen consumption this way, using multiple regression. The Dynamic Energy Budget
Dynamic energy budget
The Dynamic Energy Budget theory aims to identify simple quantitative rules for the organization of metabolism of individual organisms that can be understood from basic first principles...
theory explains why this procedure is correct. Of course, heat generated by living organisms may also be measured by direct calorimetry, in which the entire organism is placed inside the calorimeter for the measurement.
A widely used modern instrument is the differential scanning calorimeter, a device which allows thermal data to be obtained on small amounts of material. It involves heating the sample at a controlled rate and recording the heat flow either into or from the specimen.
Basic classical calculation with respect to volume
Calorimetry requires that the material being heated have known definite thermal constitutive properties. The classical rule, recognized by ClausiusRudolf Clausius
Rudolf Julius Emanuel Clausius , was a German physicist and mathematician and is considered one of the central founders of the science of thermodynamics. By his restatement of Sadi Carnot's principle known as the Carnot cycle, he put the theory of heat on a truer and sounder basis...
and by Kelvin
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
, is that the pressure exerted by the calorimetric material is fully and rapidly determined solely by its temperature and volume; this rule is for changes that do not involve phase change, such as melting of ice. There are many materials that do not comply with this rule, and for them, the present formula of classical calorimetry does not provide an adequate account. Here the classical rule is assumed to hold for the calorimetric material being used, and the propositions are mathematically written:
The thermal response of the calorimetric material is fully described by its pressure
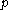 as the value of its constitutive function
as the value of its constitutive function 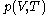 of just the volume
of just the volume 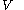 and the temperature
and the temperature 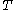 . All increments are here required to be very small.
. All increments are here required to be very small.When a small increment of heat is gained by a calorimetric body, with small increments,
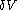 of its volume, and
of its volume, and 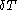 of its temperature, the increment of heat,
of its temperature, the increment of heat, 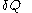 , gained by the body of calorimetric material, is given by
, gained by the body of calorimetric material, is given by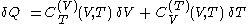
where
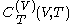 denotes the latent heat with respect to volume, of the calorimetric material at constant temperature, while the pressure and volume of the material are allowed to vary freely, at volume
denotes the latent heat with respect to volume, of the calorimetric material at constant temperature, while the pressure and volume of the material are allowed to vary freely, at volume 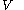 and temperature
and temperature 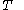 .
.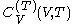 denotes the heat capacity, of the calorimetric material at constant volume, while the pressure and temperature of the material are allowed to vary freely, at volume
denotes the heat capacity, of the calorimetric material at constant volume, while the pressure and temperature of the material are allowed to vary freely, at volume 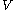 and temperature
and temperature 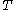 . It is customary to write
. It is customary to write 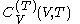 simply as
simply as 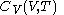 , or even more briefly as
, or even more briefly as 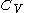 .
.The latent heat with respect to volume is the heat required for unit increment in volume at constant temperature. It can be said to be 'measured along an isotherm', and the pressure the material exerts is allowed to vary freely, according to its constitutive law
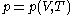 . For a given material, it can have a positive or negative sign or exceptionally it can be zero, and this can depend on the temperature, as it does for water about 4 C. The concept of latent heat with respect to volume was perhaps first recognized by Joseph Black
. For a given material, it can have a positive or negative sign or exceptionally it can be zero, and this can depend on the temperature, as it does for water about 4 C. The concept of latent heat with respect to volume was perhaps first recognized by Joseph BlackJoseph Black
Joseph Black FRSE FRCPE FPSG was a Scottish physician and chemist, known for his discoveries of latent heat, specific heat, and carbon dioxide. He was professor of Medicine at University of Glasgow . James Watt, who was appointed as philosophical instrument maker at the same university...
in 1762. The term 'latent heat of expansion' is also used. The latent heat with respect to volume can also be called the 'latent energy with respect to volume'. For all of these usages of 'latent heat', a more systematic terminology uses 'latent heat capacity'.
The heat capacity at constant volume is the heat required for unit increment in temperature at constant volume. It can be said to be 'measured along an isochor', and again, the pressure the material exerts is allowed to vary freely. It always has a positive sign. This means that for an increase in the temperature of a body without change of its volume, heat must be supplied to it. This is consistent with common experience.
Quantities like
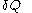 are sometimes called 'curve differentials', because they are measured along curves in the
are sometimes called 'curve differentials', because they are measured along curves in the  surface.
surface.Constant-volume calorimetry (Bomb Calorimetry)
Constant-volume calorimetry is calorimetry performed at a constant volumeVolume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
. This involves the use of a constant-volume calorimeter. Heat is still measured by the above-stated principle of calorimetry.
This means that in a suitably constructed calorimeter, the increment of volume
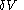 can be made to vanish,
can be made to vanish, 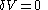 . For constant-volume calorimetry:
. For constant-volume calorimetry: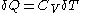
where
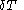 denotes the increment in temperature
denotes the increment in temperatureTemperature
Temperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
and
 denotes the heat capacity
denotes the heat capacityHeat capacity
Heat capacity , or thermal capacity, is the measurable physical quantity that characterizes the amount of heat required to change a substance's temperature by a given amount...
at constant volume.
Classical heat calculation with respect to pressure
From the above rule of calculation of heat with respect to volume, there follows one with respect to pressure.In a process of small increments,
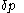 of its pressure, and
of its pressure, and 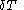 of its temperature, the increment of heat,
of its temperature, the increment of heat, 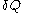 , gained by the body of calorimetric material, is given by
, gained by the body of calorimetric material, is given by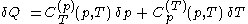
where
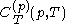 denotes the latent heat with respect to pressure, of the calorimetric material at constant temperature, while the volume and pressure of the body are allowed to vary freely, at pressure
denotes the latent heat with respect to pressure, of the calorimetric material at constant temperature, while the volume and pressure of the body are allowed to vary freely, at pressure 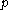 and temperature
and temperature 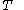 ;
;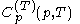 denotes the heat capacity, of the calorimetric material at constant pressure, while the temperature and volume of the body are allowed to vary freely, at pressure
denotes the heat capacity, of the calorimetric material at constant pressure, while the temperature and volume of the body are allowed to vary freely, at pressure 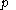 and temperature
and temperature 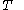 . It is customary to write
. It is customary to write 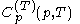 simply as
simply as 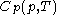 , or even more briefly as
, or even more briefly as 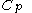 .
.The new quantities here are related to the previous ones:

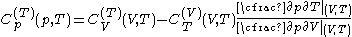
where
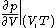 denotes the partial derivative
denotes the partial derivativePartial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
of
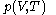 with respect to
with respect to 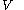 evaluated for
evaluated for 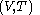
and
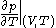 denotes the partial derivative of
denotes the partial derivative of 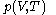 with respect to
with respect to 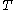 evaluated for
evaluated for 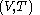 .
.The latent heats
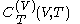 and
and 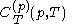 are always of opposite sign.
are always of opposite sign.It is common to refer to the ratio of specific heats as
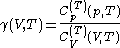 often just written as
often just written as 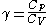 .
.Cumulation of heating
For a time-dependent process of heating of the calorimetric material, defined by a continuous joint progression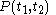 of
of 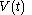 and
and 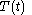 , starting at time
, starting at time 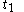 and ending at time
and ending at time 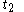 , there can be calculated an accumulated quantity of heat delivered,
, there can be calculated an accumulated quantity of heat delivered, 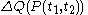 . This calculation is done by mathematical integration along the progression
. This calculation is done by mathematical integration along the progressionLine integral
In mathematics, a line integral is an integral where the function to be integrated is evaluated along a curve.The function to be integrated may be a scalar field or a vector field...
with respect to time. This is because increments of heat are 'additive'; but this does not mean that heat is a conservative quantity. The idea that heat was a conservative quantity was invented by Lavoisier
Antoine Lavoisier
Antoine-Laurent de Lavoisier , the "father of modern chemistry", was a French nobleman prominent in the histories of chemistry and biology...
, and is called the 'caloric theory
Caloric theory
The caloric theory is an obsolete scientific theory that heat consists of a self-repellent fluid called caloric that flows from hotter bodies to colder bodies. Caloric was also thought of as a weightless gas that could pass in and out of pores in solids and liquids...
'; by the middle of the nineteenth century it was recognized as mistaken. Written with the symbol
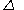 , the quantity
, the quantity 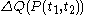 is not at all restricted to be an increment with very small values; this is in contrast with
is not at all restricted to be an increment with very small values; this is in contrast with 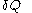 .
.One can write
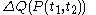
-
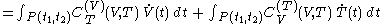 .
.
This expression uses quantities such as
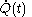 which are defined in the section below headed 'Mathematical aspects of the above rules'.
which are defined in the section below headed 'Mathematical aspects of the above rules'.Mathematical aspects of the above rules
The use of 'very small' quantities such as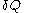 is related to the physical requirement for the quantity
is related to the physical requirement for the quantity 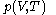 to be 'rapidly determined' by
to be 'rapidly determined' by 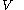 and
and 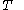 ; such 'rapid determination' refers to a physical process. These 'very small' quantities are used in the Leibniz
; such 'rapid determination' refers to a physical process. These 'very small' quantities are used in the LeibnizGottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
approach to the infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
. The Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
approach uses instead 'fluxion
Fluxion
Fluxion may refer to:* An alternate spelling of fluxon, a quantum of magnetic flux, such as in a superconductor* Fluxion was Isaac Newton's term for the derivative of a "fluent", or continuous function....
s' such as
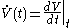 , which makes it more obvious that
, which makes it more obvious that  must be 'rapidly determined'.
must be 'rapidly determined'.In terms of fluxions, the above first rule of calculation can be written
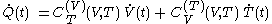
where
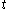 denotes the time
denotes the time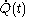 denotes the time rate of heating of the calorimetric material at time
denotes the time rate of heating of the calorimetric material at time 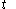
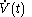 denotes the time rate of change of volume of the calorimetric material at time
denotes the time rate of change of volume of the calorimetric material at time 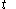
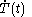 denotes the time rate of change of temperature of the calorimetric material.
denotes the time rate of change of temperature of the calorimetric material.The increment
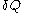 and the fluxion
and the fluxion 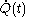 are obtained for a particular time
are obtained for a particular time 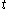 that determines the values of the quantities on the righthand sides of the above rules. But this is not a reason to expect that there should exist a mathematical function
that determines the values of the quantities on the righthand sides of the above rules. But this is not a reason to expect that there should exist a mathematical functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
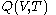 . For this reason, the increment
. For this reason, the increment 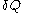 is said to be an 'imperfect differential' or an 'inexact differential
is said to be an 'imperfect differential' or an 'inexact differentialInexact differential
An inexact differential or imperfect differential is a specific type of differential used in thermodynamics to express the path dependence of a particular differential. It is contrasted with the concept of the exact differential in calculus, which can be expressed as the gradient of another...
'. Some books indicate this by writing
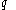 instead of
instead of 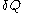 . Also, the notation đQ is used in some books. Carelessness about this can lead to error.
. Also, the notation đQ is used in some books. Carelessness about this can lead to error.The quantity
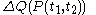 is properly said to be a functional
is properly said to be a functionalFunctional (mathematics)
In mathematics, and particularly in functional analysis, a functional is a map from a vector space into its underlying scalar field. In other words, it is a function that takes a vector as its input argument, and returns a scalar...
of the continuous joint progression
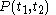 of
of 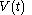 and
and 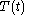 , but, in the mathematical definition of a function
, but, in the mathematical definition of a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
,
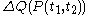 is not a function of
is not a function of 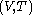 . Although the fluxion
. Although the fluxion 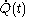 is defined here as a function of time
is defined here as a function of time 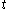 , the symbols
, the symbols 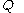 and
and 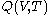 respectively standing alone are not defined here.
respectively standing alone are not defined here.Physical scope of the above rules of calorimetry
The above rules refer only to suitable calorimetric materials. The terms 'rapidly' and 'very small' call for empirical physical checking of the domain of validity of the above rules.The above rules for the calculation of heat belong to pure calorimetry. They make no reference to thermodynamics
Thermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
, and were mostly understood before the advent of thermodynamics. They are the basis of the 'thermo' contribution to thermodynamics. The 'dynamics' contribution is based on the idea of work, which is not used in the above rules of calculation.
Experimentally conveniently measured coefficients
Empirically, it is convenient to measure properties of calorimetric materials under experimentally controlled conditions.Pressure increase at constant volume
For measurements at experimentally controlled volume, one can use the assumption, stated above, that the pressure of the body of calorimetric material is can be expressed as a function of its volume and temperature.For measurement at constant experimentally controlled volume, the isochoric coefficient of pressure rise with temperature, is defined by
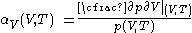 .
.Expansion at constant pressure
For measurements at experimentally controlled pressure, it is assumed that the volume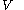 of the body of calorimetric material can be expressed as a function
of the body of calorimetric material can be expressed as a function 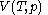 of its temperature
of its temperature 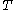 and pressure
and pressure 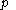 . This assumption is related to, but is not the same as, the above used assumption that the pressure of the body of calorimetric material is known as a function of its volume and temperature; anomalous behaviour of materials can affect this relation.
. This assumption is related to, but is not the same as, the above used assumption that the pressure of the body of calorimetric material is known as a function of its volume and temperature; anomalous behaviour of materials can affect this relation.The quantity that is conveniently measured at constant experimentally controlled pressure, the isobaric volume expansion coefficient, is defined by
 .
.Compressibility at constant temperature
For measurements at experimentally controlled temperature, it is again assumed that the volume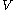 of the body of calorimetric material can be expressed as a function
of the body of calorimetric material can be expressed as a function 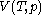 of its temperature
of its temperature 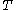 and pressure
and pressure 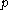 , with the same provisos as mentioned just above.
, with the same provisos as mentioned just above.The quantity that is conveniently measured at constant experimentally controlled temperature, the isothermal compressibility, is defined by
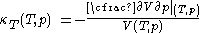 .
.Relation between classical calorimetric quantities
Assuming that the rule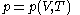 is known, one can derive the function
is known, one can derive the function 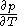 that is used above in the classical heat calculation with respect to pressure. This function can be found experimentally from the coefficients
that is used above in the classical heat calculation with respect to pressure. This function can be found experimentally from the coefficients 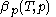 and
and 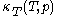 through the mathematically deducible relation
through the mathematically deducible relation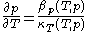 .
.Connection between calorimetry and thermodynamics
ThermodynamicsThermodynamics
Thermodynamics is a physical science that studies the effects on material bodies, and on radiation in regions of space, of transfer of heat and of work done on or by the bodies or radiation...
developed gradually over the first half of the nineteenth century, building on the above theory of calorimetry which had been worked out before it, and on other discoveries. According to Gislason and Craig (2005): "Most thermodynamic data come from calorimetry..." According to Kondepudi (2008): "Calorimetry is widely used in present day laboratories."
In terms of thermodynamics, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
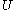 of the calorimetric material can be considered as the value of a function
of the calorimetric material can be considered as the value of a function 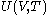 of
of 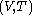 , with partial derivatives
, with partial derivatives 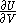 and
and 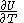 .
.Then it can be shown that one can write a thermodynamic version of the above calorimetric rules:
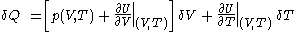
with
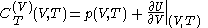
and
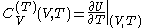 .
.Again, further in terms of thermodynamics, the internal energy
Internal energy
In thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
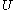 of the calorimetric material can sometimes, depending on the calorimetric material, be considered as the value of a function
of the calorimetric material can sometimes, depending on the calorimetric material, be considered as the value of a function 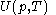 of
of 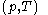 , with partial derivatives
, with partial derivatives 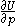 and
and 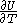 , and with
, and with 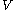 being expressible as the value of a function
being expressible as the value of a function 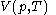 of
of 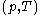 , with partial derivatives
, with partial derivatives 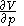 and
and 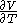 .
.Then, according to Adkins (1975), it can be shown that one can write a further thermodynamic version of the above calorimetric rules:
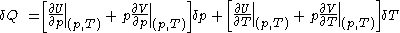
with
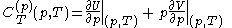
and
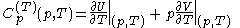 .
.Beyond the calorimetric fact noted above that the latent heats
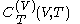 and
and 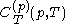 are always of opposite sign, it may be shown, using the thermodynamic concept of work, that also
are always of opposite sign, it may be shown, using the thermodynamic concept of work, that also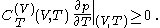
Special interest of thermodynamics in calorimetry: the isothermal segments of a Carnot cycle
Calorimetry has a special benefit for thermodynamics. It tells about the heat absorbed or emitted in the isothermal segment of a Carnot cycleCarnot cycle
The Carnot cycle is a theoretical thermodynamic cycle proposed by Nicolas Léonard Sadi Carnot in 1824 and expanded by Benoit Paul Émile Clapeyron in the 1830s and 40s. It can be shown that it is the most efficient cycle for converting a given amount of thermal energy into work, or conversely,...
.
A Carnot cycle is a special kind of cyclic process affecting a body composed of material suitable for use in a heat engine. Such a material is of the kind considered in calorimetry, as noted above, that exerts a pressure that is very rapidly determined just by temperature and volume. Such a body is said to change reversibly. A Carnot cycle consists of four successive stages or segments:
(1) a change in volume from a volume
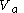 to a volume
to a volume 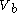 at constant temperature
at constant temperature 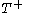 so as to incur a flow of heat into the body (known as an isothermal change)
so as to incur a flow of heat into the body (known as an isothermal change)(2) a change in volume from
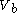 to a volume
to a volume 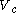 at a variable temperature just such as to incur no flow of heat (known as an adiabatic change)
at a variable temperature just such as to incur no flow of heat (known as an adiabatic change)(3) another isothermal change in volume from
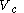 to a volume
to a volume 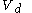 at constant temperature
at constant temperature  such as to incur a flow or heat out of the body and just such as to precisely prepare for the following change
such as to incur a flow or heat out of the body and just such as to precisely prepare for the following change(4) another adiabatic change of volume from
 back to
back to 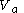 just such as to return the body to its starting temperature
just such as to return the body to its starting temperature 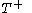 .
.In isothermal segment (1), the heat that flows into the body is given by
and in isothermal segment (3) the heat that flows out of the body is given by
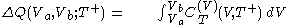 .
.Because the segments (2) and (4) are adiabats, no heat flows into or out of the body during them, and consequently the net heat supplied to the body during the cycle is given by
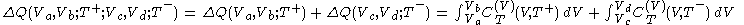 .
.This quantity is used by thermodynamics and is related in a special way to the net work
Work (thermodynamics)
In thermodynamics, work performed by a system is the energy transferred to another system that is measured by the external generalized mechanical constraints on the system. As such, thermodynamic work is a generalization of the concept of mechanical work in mechanics. Thermodynamic work encompasses...
done by the body during the Carnot cycle. The net change of the body's internal energy during the Carnot cycle,
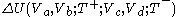 , is equal to zero, because the material of the working body has the special properties noted above.
, is equal to zero, because the material of the working body has the special properties noted above.Special interest of calorimetry in thermodynamics: relations between classical calorimetric quantities
Relation of latent heat with respect to volume, and the equation of state
The quantity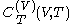 , the latent heat with respect to volume, belongs to classical calorimetry. It accounts for the occurrence of energy transfer by work in a process in which heat is also transferred; the quantity, however, was considered before the relation between heat and work transfers was clarified by the invention of thermodynamics. In the light of thermodynamics, the classical calorimetric quantity is revealed as being tightly linked to the calorimetric material's equation of state
, the latent heat with respect to volume, belongs to classical calorimetry. It accounts for the occurrence of energy transfer by work in a process in which heat is also transferred; the quantity, however, was considered before the relation between heat and work transfers was clarified by the invention of thermodynamics. In the light of thermodynamics, the classical calorimetric quantity is revealed as being tightly linked to the calorimetric material's equation of state 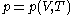 . Provided that the temperature
. Provided that the temperature 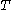 is measured in the thermodynamic absolute scale, the relation is expressed in the formula
is measured in the thermodynamic absolute scale, the relation is expressed in the formula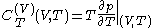 .
.Difference of specific heats
Advanced thermodynamics provides the relation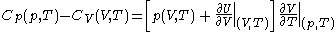 .
.From this, further mathematical and thermodynamic reasoning leads to another relation between classical calorimetric quantities. The difference of specific heats is given by
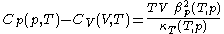 .
.Books
- Adkins, C.J. (1975). Equilibrium Thermodynamics, second edition, McGraw-Hill, London, ISBN 0-07-084057-1.
- Bailyn, M. (1994). A Survey of Thermodynamics, American Institute of Physics, New York, ISBN 0-88318-797-3.
- Callen, H.B. (1960/1985). Thermodynamics and an Introduction to Thermostatistics, second edition, Wiley, New York, ISBN 9812-53-185-8.
- Guggenheim, E.A. (1949/1967). Thermodynamics. An Advanced Treatment for Chemists and Physicists, North-Holland, Amsterdam.
- Iribarne, J.V., Godson, W.L. (1973/1981), Atmospheric Thermodynamics, second edition, D. Reidel, Kluwer Academic Publishers, Dordrecht, ISBN 90-277-1296-4.
- Kondepudi, D. (2008). Introduction to Modern Thermodynamics, Wiley, Chichester, ISBN 978-0-470-01598-8.
- Landsberg, P.T. (1978). Thermodynamics and Statistical Mechanics, Oxford University Press, Oxford, ISBN 0-19-851142-6.
- Lewis, G.N., Randall, M. (1923/1961). Thermodynamics, second edition revised by K.S Pitzer, L. Brewer, McGraw-Hill, New York.
- Maxwell, J.C. (1872). Theory of Heat, third edition, Longmans, Green, and Co., London.
- Planck, M. (1923/1926). Treatise on Thermodynamics, third English edition translated by A. Ogg from the seventh German edition, Longmans, Green & Co., London.
- Truesdell, C., Bharatha, S. (1977). The Concepts and Logic of Classical Thermodynamics as a Theory of Heat Engines, Rigorously Constructed upon the Foundation Laid by S. Carnot and F. Reech, Springer, New York, ISBN 0-387-07971-8.