Cantor's diagonal argument, also called the diagonalisation argument, the diagonal slash argument or the diagonal method, was published in 1891 by Georg Cantor

Georg Cantor

Georg Ferdinand Ludwig Philipp Cantor was a German mathematician, best known as the inventor of set theory, which has become a fundamental theory in mathematics. Cantor established the importance of one-to-one correspondence between the members of two sets, defined infinite and well-ordered sets,...

 as a mathematical proof

Mathematical proof

In mathematics, a proof is a convincing demonstration that some mathematical statement is necessarily true. Proofs are obtained from deductive reasoning, rather than from inductive or empirical arguments. That is, a proof must demonstrate that a statement is true in all cases, without a single...

 that there are infinite sets which cannot be put into one-to-one correspondence

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

 with the infinite set of natural number

Natural number

In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...

s. Such sets are now known as uncountable set

Uncountable set

In mathematics, an uncountable set is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers.-Characterizations:There...

s, and the size of infinite sets is now treated by the theory of cardinal number

Cardinal number

In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...

s which Cantor began.

The diagonal argument was not Cantor's first proof

Cantor's first uncountability proof

Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...

 of the uncountability of the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s; it was actually published much later than his first proof, which appeared in 1874. However, it demonstrates a powerful and general technique that has since been used in a wide range of proofs, also known as diagonal arguments by analogy with the argument used in this proof. The most famous examples are perhaps Russell's paradox

Russell's paradox

In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...

, the first of Gödel's incompleteness theorems

Gödel's incompleteness theorems

Gödel's incompleteness theorems are two theorems of mathematical logic that establish inherent limitations of all but the most trivial axiomatic systems capable of doing arithmetic. The theorems, proven by Kurt Gödel in 1931, are important both in mathematical logic and in the philosophy of...

, and Turing's answer to the Entscheidungsproblem

Entscheidungsproblem

In mathematics, the is a challenge posed by David Hilbert in 1928. The asks for an algorithm that will take as input a description of a formal language and a mathematical statement in the language and produce as output either "True" or "False" according to whether the statement is true or false...

.

An uncountable set

Cantor's original proof considers an infinite sequence

Sequence

In mathematics, a sequence is an ordered list of objects . Like a set, it contains members , and the number of terms is called the length of the sequence. Unlike a set, order matters, and exactly the same elements can appear multiple times at different positions in the sequence...

 S of the form (s₁, s₂, s₃, ...) where each element s_i is an infinite sequence of 1's or 0's. This sequence is countable, as to every natural number n we associate one and only one element of the sequence. We might write such a sequence as a numbered list:

s₁ = (0, 0, 0, 0, 0, 0, 0, ...)

s₂ = (1, 1, 1, 1, 1, 1, 1, ...)

s₃ = (0, 1, 0, 1, 0, 1, 0, ...)

s₄ = (1, 0, 1, 0, 1, 0, 1, ...)

s₅ = (1, 1, 0, 1, 0, 1, 1, ...)

s₆ = (0, 0, 1, 1, 0, 1, 1, ...)

s₇ = (1, 0, 0, 0, 1, 0, 0, ...)

...

For each m and n let s_n,m be the m^th element of the n^th sequence on the list. So, for instance, s_2,1 is the first element of the second sequence.

It is possible to build a sequence s₀ in such a way that its first element is different from the first element of the first sequence in the list, its second element is different from the second element of the second sequence in the list, and, in general, its n^th element is different from the n^th element of the n^th sequence in the list. That is to say, if s_n,n is 1, then s_0,n is 0, otherwise s_0,n is 1. For instance:

s₁ = (0, 0, 0, 0, 0, 0, 0, ...)

s₂ = (1, 1, 1, 1, 1, 1, 1, ...)

s₃ = (0, 1, 0, 1, 0, 1, 0, ...)

s₄ = (1, 0, 1, 0, 1, 0, 1, ...)

s₅ = (1, 1, 0, 1, 0, 1, 1, ...)

s₆ = (0, 0, 1, 1, 0, 1, 1, ...)

s₇ = (1, 0, 0, 0, 1, 0, 0, ...)

...

s₀ = (1, 0, 1, 1, 1, 0, 1, ...)

The elements s_1,1, s_2,2, s_3,3, and so on, are here highlighted, showing the origin of the name "diagonal argument". Each element in s₀ is, by definition, different from the highlighted element in the corresponding column of the table above it. In short, s_0,n ≠ s_n,n.

Therefore this new sequence s₀ is distinct from all the sequences in the list. This follows from the fact that if it were identical to, say, the 10th sequence in the list, then we would have s_0,10 = s_10,10. In general, we would have s_0,n = sn,n, which, due to the construction of s₀, is impossible. In short, by its definition s₀ is not contained in the countable sequence S.

Let T be a set consisting of all infinite sequences of 0s and 1s. By its definition, this set must contain not only the sequences included in S, but also s₀, which is just another sequence of 0s and 1s. However, s₀ does not appear anywhere in S. Hence, T cannot coincide with S.

Because this argument applies to any countable set S of sequences of 0s and 1s, it follows that T cannot be equal to any such set. Thus T is uncountable: it cannot be placed in one-to-one correspondence with the set of natural numbers .

Interpretation

The interpretation of Cantor's result will depend upon one's view of mathematics. To constructivists

Constructivism (mathematics)

In the philosophy of mathematics, constructivism asserts that it is necessary to find a mathematical object to prove that it exists. When one assumes that an object does not exist and derives a contradiction from that assumption, one still has not found the object and therefore not proved its...

, the argument shows no more than that there is no bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

 between the natural numbers and T. It does not rule out the possibility that the latter are subcountable. In the context of classical mathematics

Classical mathematics

In the foundations of mathematics, classical mathematics refers generally to the mainstream approach to mathematics, which is based on classical logic and ZFC set theory. It stands in contrast to other types of mathematics such as constructive mathematics or predicative mathematics; theories other...

, this is impossible, and the diagonal argument establishes that, although both sets are infinite, there are actually more infinite sequences of ones and zeros than there are natural numbers.

Real numbers

The uncountability of the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s was already established by Cantor's first uncountability proof

Cantor's first uncountability proof

Georg Cantor's first uncountability proof demonstrates that the set of all real numbers is uncountable. This proof differs from the more familiar proof that uses his diagonal argument...

, but it also follows from the above result. To see this, we will build a one-to-one correspondence between the set T of infinite binary strings and a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of R (the set of real numbers). Since T is uncountable, this subset of R must be uncountable. Hence R is uncountable.

To build this one-to-one correspondence (or bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

), observe that the string 0111… appears after the binary point in the binary expansion 0.0111…. This suggests defining the function f(t) = 0.t, where t is a string in T. Unfortunately, f(1000…) = 0.1000… = 1/2, and f(0111…) = 0.0111… = 1/4 + 1/8 + 1/16 + … = 1/2. So this function is not a bijection since two strings correspond to one number—a number having two binary expansions.

However, modifying this function produces a bijection from T to the interval

Interval (mathematics)

In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...

 (0, 1)—that is, the real numbers > 0 and < 1. The idea is to remove the "problem" elements from T and (0, 1), and handle them separately. From (0, 1), remove the numbers having two binary expansions. Put these numbers in a sequence: a = (1/2, 1/4, 3/4, 1/8, 3/8, 5/8, 7/8, …). From T, remove the strings appearing after the binary point in the binary expansions of 0, 1, and the numbers in sequence a. Put these eventually-constant strings in a sequence: b = (000…, 111…, 1000…, 0111…, 01000…, 00111…, …). A bijection g(t) from T to (0, 1) is defined by: If t is the n^th string in sequence b, let g(t) be the n^th number in sequence a; otherwise, let g(t) = 0.t.

To build a bijection from T to R: start with the tangent function tan(x), which provides a bijection from (−π/2, π/2) to R. Next observe that the linear function

Linear function

In mathematics, the term linear function can refer to either of two different but related concepts:* a first-degree polynomial function of one variable;* a map between two vector spaces that preserves vector addition and scalar multiplication....

 h(x) = πx - π/2 provides a bijection from (0, 1) to (−π/2, π/2). The composite function

Function composition

In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...

 tan(h(x)) = tan(πx - π/2) provides a bijection from (0, 1) to R. Compose this function with g(t) to obtain tan(h(g(t))) = tan(πg(t) - π/2), which is a bijection from T to R. This means that T and R have the same cardinality—this cardinality is called the "cardinality of the continuum

Cardinality of the continuum

In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....

."

General sets

A generalized form of the diagonal argument was used by Cantor to prove Cantor's theorem

Cantor's theorem

In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...

: for every set S the power set of S, i.e., the set of all subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

s of S (here written as P(S)), is larger than S itself. This proof proceeds as follows:

Let f be any function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 from S to P(S). It suffices to prove f cannot be surjective. That means that some member of P(S), i.e., some subset of S, is not in the image

Image (mathematics)

In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...

 of f. Consider the set:


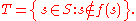
For every s in S, either s is in T or not. If s is in T, then by definition of T, s is not in f(s), so T is not equal to f(s). On the other hand, if s is not in T, then by definition of T, s is in f(s), so again T is not equal to f(s).
For a more complete account of this proof, see Cantor's theorem

Cantor's theorem

In elementary set theory, Cantor's theorem states that, for any set A, the set of all subsets of A has a strictly greater cardinality than A itself...

.

Consequences

This result implies that the notion of the set of all sets is an inconsistent notion. If S were the set of all sets then P(S) would at the same time be bigger than S and a subset of S.

Russell's Paradox

Russell's paradox

In the foundations of mathematics, Russell's paradox , discovered by Bertrand Russell in 1901, showed that the naive set theory created by Georg Cantor leads to a contradiction...

 has shown us that naive set theory

Naive set theory

Naive set theory is one of several theories of sets used in the discussion of the foundations of mathematics. The informal content of this naive set theory supports both the aspects of mathematical sets familiar in discrete mathematics , and the everyday usage of set theory concepts in most...

, based on an unrestricted comprehension scheme, is contradictory. Note that there is a similarity between the construction of T and the set in Russell's paradox. Therefore, depending on how we modify the axiom scheme of comprehension in order to avoid Russell's paradox, arguments such as the non-existence of a set of all sets may or may not remain valid.

The diagonal argument shows that the set of real numbers is "bigger" than the set of natural numbers (and therefore, the integers and rationals as well). Therefore, we can ask if there is a set whose cardinality is "between" that of the integers and that of the reals. This question leads to the famous continuum hypothesis

Continuum hypothesis

In mathematics, the continuum hypothesis is a hypothesis, advanced by Georg Cantor in 1874, about the possible sizes of infinite sets. It states:Establishing the truth or falsehood of the continuum hypothesis is the first of Hilbert's 23 problems presented in the year 1900...

. Similarly, the question of whether there exists a set whose cardinality is between |S| and |P(S)| for some infinite S leads to the generalized continuum hypothesis.

Analogues of the diagonal argument are widely used in mathematics to prove the existence or nonexistence of certain objects. For example, the conventional proof of the unsolvability of the halting problem

Halting problem

In computability theory, the halting problem can be stated as follows: Given a description of a computer program, decide whether the program finishes running or continues to run forever...

 is essentially a diagonal argument. Also, diagonalization was originally used to show the existence of arbitrarily hard complexity classes and played a key role in early attempts to prove P does not equal NP. In 2008, diagonalization was used to "slam the door" on Laplace's demon

Laplace's demon

In the history of science, Laplace's demon was the first published articulation of causal or scientific determinism by Pierre-Simon Laplace in 1814...

.

Version for Quine's New Foundations

The above proof fails for W. V. Quine's "New Foundations

New Foundations

In mathematical logic, New Foundations is an axiomatic set theory, conceived by Willard Van Orman Quine as a simplification of the theory of types of Principia Mathematica. Quine first proposed NF in a 1937 article titled "New Foundations for Mathematical Logic"; hence the name...

" set theory (NF). In NF, the naive axiom scheme of comprehension is modified to avoid the paradoxes by introducing a kind of "local" type theory

Type theory

In mathematics, logic and computer science, type theory is any of several formal systems that can serve as alternatives to naive set theory, or the study of such formalisms in general...

. In this axiom scheme,


is not a set — i.e., does not satisfy the axiom scheme. On the other hand, we might try to create a modified diagonal argument by noticing that


is a set in NF. In which case, if P₁(S) is the set of one-element subsets of S and f is a proposed bijection from P₁(S) to P(S), one is able to use reductio to prove that |P₁(S)| < |P(S)|.

The proof follows by the fact that if f were indeed a map onto P(S)), then we could find r in S, such that f({r}) coincides with the modified diagonal set, above. We would conclude that if r is not in f({r}), then r is in f({r}) and vice-versa.

It is not possible to put P₁(S) in a one-to-one relation with S, as the two have different types, and so any function so defined would violate the typing rules for the comprehension scheme.

External links

• Cantor's Diagonal Proof at MathPages

The source of this article is wikipedia, the free encyclopedia.  The text of this article is licensed under the GFDL.