
Carathéodory's extension theorem
Encyclopedia
In measure theory, Carathéodory's extension theorem (named after the Greek
mathematician
Constantin Carathéodory
) states that any σ-finite measure defined on a given ring R of subsets of a given set Ω can be uniquely extended to the σ-algebra generated by R. Consequently, any measure on a space containing all interval
s of real number
s can be extended to the Borel algebra
of the set of real numbers. This is an extremely powerful result of measure theory, and proves for example the existence of the Lebesgue measure
.
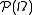 , the power set of Ω, which has the following properties:
, the power set of Ω, which has the following properties:
With the same notation, we define a ring R as a subset of the power set of Ω which has the following properties:
Thus any ring on Ω is also a semi-ring.
Sometimes, the following constraint is added in the measure theory context:
(R(S) is simply the set containing all finite unions of sets in S).
In addition, it can be proved that μ is a pre-measure
if and only if the extended content is also a pre-measure, and that any pre-measure on R(S) that extends the pre-measure on S is necessarily of this form.
generated by them. The idea is that it is possible to build a pre-measure on a semi-ring S (for example Stieltjes measures), which can then be extended to a pre-measure on R(S), which can finally be extended to a measure
on a σ-algebra through Caratheodory's extension theorem. As σ-algebras generated by semi rings and rings are the same, the difference does not really matter (in the measure theory context at least). Actually, the Carathéodory's extension theorem can be slightly generalized by replacing ring by semi-ring.
The definition of semi-ring may seem a bit convoluted, but the following example shows why it is useful.
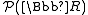 defined by the set of all half-open intervals [a, b) for a and b reals. This is a semi-ring, but not a ring. Stieltjes measures are defined on intervals; the countable additivity on the semi ring is not too difficult to prove because we only consider countable unions of intervals which are intervals themselves. Proving it for arbitrary countably union of intervals is proved using Caratheodory's theorem.
defined by the set of all half-open intervals [a, b) for a and b reals. This is a semi-ring, but not a ring. Stieltjes measures are defined on intervals; the countable additivity on the semi ring is not too difficult to prove because we only consider countable unions of intervals which are intervals themselves. Proving it for arbitrary countably union of intervals is proved using Caratheodory's theorem.
on a R.
The Carathéodory's extension theorem states that there exists a measure such that is an extension of μ. (That is).
Here σ(R) is the σ-algebra
generated by R.
If μ is σ-finite then the extension is unique (and also σ-finite).
Greeks
The Greeks, also known as the Hellenes , are a nation and ethnic group native to Greece, Cyprus and neighboring regions. They also form a significant diaspora, with Greek communities established around the world....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Constantin Carathéodory
Constantin Carathéodory
Constantin Carathéodory was a Greek mathematician. He made significant contributions to the theory of functions of a real variable, the calculus of variations, and measure theory...
) states that any σ-finite measure defined on a given ring R of subsets of a given set Ω can be uniquely extended to the σ-algebra generated by R. Consequently, any measure on a space containing all interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
s of real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
s can be extended to the Borel algebra
Borel algebra
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of the set of real numbers. This is an extremely powerful result of measure theory, and proves for example the existence of the Lebesgue measure
Lebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
.
Definitions
For a given set Ω, we may define a semi-ring as a subset S of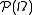 , the power set of Ω, which has the following properties:
, the power set of Ω, which has the following properties:- For all , we have (closed under pairwise intersections)
- For all , there exist disjoint sets , with , such that
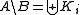 (relative complementsComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
(relative complementsComplement (set theory)In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
can be written as finite disjoint unions).
With the same notation, we define a ring R as a subset of the power set of Ω which has the following properties:
- For all , we have (closed under pairwise unions)
- For all , we have (closed under relative complements).
Thus any ring on Ω is also a semi-ring.
Sometimes, the following constraint is added in the measure theory context:
- Ω is the disjoint union of a countable family of sets in S.
Properties
- Arbitrary (possibly uncountable) intersections of rings on Ω are still rings on Ω.
- If A is a non-empty subset of
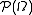 , then we define the ring generated by A (noted R(A)) as the smallest ring containing A. It is straightfoward to see that the ring generated by A is equivalent to the intersection of all rings containing A.
, then we define the ring generated by A (noted R(A)) as the smallest ring containing A. It is straightfoward to see that the ring generated by A is equivalent to the intersection of all rings containing A. - For a semi-ring S, the set containing all finite disjoint union of sets of S is the ring generated by S:
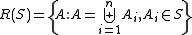
(R(S) is simply the set containing all finite unions of sets in S).
- A content μ defined on a semi-ring S can be extended on the ring generated by S. Such an extension is unique. The extended content can be written:
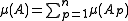 for
for 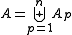 , with the Ap in S.
, with the Ap in S.
In addition, it can be proved that μ is a pre-measure
Pre-measure
In mathematics, a pre-measure is a function that is, in some sense, a precursor to a bona fide measure on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory, where they can be used to define measures such as Hausdorff measure and packing measure on metric...
if and only if the extended content is also a pre-measure, and that any pre-measure on R(S) that extends the pre-measure on S is necessarily of this form.
Motivation
In measure theory, we are not interested in semi-rings and rings themselves, but rather in σ-algebrasSigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by them. The idea is that it is possible to build a pre-measure on a semi-ring S (for example Stieltjes measures), which can then be extended to a pre-measure on R(S), which can finally be extended to a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
on a σ-algebra through Caratheodory's extension theorem. As σ-algebras generated by semi rings and rings are the same, the difference does not really matter (in the measure theory context at least). Actually, the Carathéodory's extension theorem can be slightly generalized by replacing ring by semi-ring.
The definition of semi-ring may seem a bit convoluted, but the following example shows why it is useful.
Example
Think about the subset of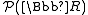 defined by the set of all half-open intervals [a, b) for a and b reals. This is a semi-ring, but not a ring. Stieltjes measures are defined on intervals; the countable additivity on the semi ring is not too difficult to prove because we only consider countable unions of intervals which are intervals themselves. Proving it for arbitrary countably union of intervals is proved using Caratheodory's theorem.
defined by the set of all half-open intervals [a, b) for a and b reals. This is a semi-ring, but not a ring. Stieltjes measures are defined on intervals; the countable additivity on the semi ring is not too difficult to prove because we only consider countable unions of intervals which are intervals themselves. Proving it for arbitrary countably union of intervals is proved using Caratheodory's theorem.Statement of the theorem
Let R be a ring on Ω and be a pre-measurePre-measure
In mathematics, a pre-measure is a function that is, in some sense, a precursor to a bona fide measure on a given space. Pre-measures are particularly useful in fractal geometry and dimension theory, where they can be used to define measures such as Hausdorff measure and packing measure on metric...
on a R.
The Carathéodory's extension theorem states that there exists a measure such that is an extension of μ. (That is).
Here σ(R) is the σ-algebra
Sigma-algebra
In mathematics, a σ-algebra is a technical concept for a collection of sets satisfying certain properties. The main use of σ-algebras is in the definition of measures; specifically, the collection of sets over which a measure is defined is a σ-algebra...
generated by R.
If μ is σ-finite then the extension is unique (and also σ-finite).
See also
- Outer measureOuter measureIn mathematics, in particular in measure theory, an outer measure or exterior measure is a function defined on all subsets of a given set with values in the extended real numbers satisfying some additional technical conditions. A general theory of outer measures was first introduced by...
: the proof of Carathéodory's extension theorem is based upon the outer measure concept. - Hahn-Kolmogorov theoremHahn-Kolmogorov theoremIn mathematics, the Hahn–Kolmogorov theorem characterizes when a finitely additive function with non-negative values can be extended to a bona fide measure. It is named after the Austrian mathematician Hans Hahn and the Russian/Soviet mathematician Andrey Kolmogorov.-Statement of the theorem:Let ...

