Cauchy number
Encyclopedia
The Cauchy number,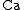 
is a dimensionless number in fluid dynamics
used in the study of compressible flows
. It is named after the French mathematician Augustin Louis Cauchy
.
When the compressibility is important the elastic forces must be considered along with inertial forces for dynamic similarity. Thus, the Cauchy Number is defined as the ratio between inertial and the compressibility force (elastic force) in a flow and can be expressed as
,
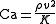where
, the Cauchy number may be expressed in terms of Mach number
. The isentropic bulk modulus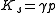
, where 
is the specific heat capacity ratio
and
is the fluid pressure.
If the fluid obeys the ideal gas law
, we have
,
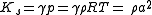where
Substituting K (K_s) in the equation for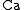
yields
.
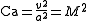Thus, the Cauchy number is square of the Mach number for isentropic flow of a perfect gas
.
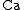is a dimensionless number in fluid dynamicsFluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
used in the study of compressible flows
Compressible flow
Compressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...
. It is named after the French mathematician Augustin Louis Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
.
When the compressibility is important the elastic forces must be considered along with inertial forces for dynamic similarity. Thus, the Cauchy Number is defined as the ratio between inertial and the compressibility force (elastic force) in a flow and can be expressed as
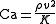,where
-
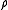= density of fluid, (SISiSi, si, or SI may refer to :- Measurement, mathematics and science :* International System of Units , the modern international standard version of the metric system...
units: kg/m3) -
= local fluid velocity, (SI units: m/s) -
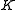= bulk modulus of elasticityBulk modulusThe bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
, (SI units: Pa)
Relation between Cauchy number and Mach number
For isentropic processesIsentropic process
In thermodynamics, an isentropic process or isoentropic process is one in which for purposes of engineering analysis and calculation, one may assume that the process takes place from initiation to completion without an increase or decrease in the entropy of the system, i.e., the entropy of the...
, the Cauchy number may be expressed in terms of Mach number
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
. The isentropic bulk modulus
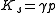, where is the specific heat capacity ratioHeat capacity ratio
The heat capacity ratio or adiabatic index or ratio of specific heats, is the ratio of the heat capacity at constant pressure to heat capacity at constant volume . It is sometimes also known as the isentropic expansion factor and is denoted by \gamma or \kappa . The latter symbol kappa is...
and
is the fluid pressure.If the fluid obeys the ideal gas law
Ideal gas law
The ideal gas law is the equation of state of a hypothetical ideal gas. It is a good approximation to the behavior of many gases under many conditions, although it has several limitations. It was first stated by Émile Clapeyron in 1834 as a combination of Boyle's law and Charles's law...
, we have
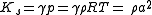,where
-
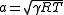= speed of sound, (SI units: m/s) -
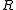= characteristic gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
, (SI units: J/(kg K) ) -
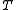= temperature, (SI units: K)
Substituting K (K_s) in the equation for
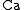yields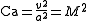.Thus, the Cauchy number is square of the Mach number for isentropic flow of a perfect gas
Ideal gas
An ideal gas is a theoretical gas composed of a set of randomly-moving, non-interacting point particles. The ideal gas concept is useful because it obeys the ideal gas law, a simplified equation of state, and is amenable to analysis under statistical mechanics.At normal conditions such as...
.