
Character variety
Encyclopedia
In the mathematics
of moduli theory, given an algebraic, reductive, Lie group
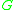 and a finitely generated group
and a finitely generated group  , the
, the 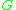 -character variety of
-character variety of  is a space of equivalence classes of group homomorphisms
is a space of equivalence classes of group homomorphisms
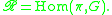
More precisely,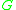 acts on
acts on 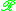 by conjugation and two homomorphisms are defined to be equivalent if and only if their orbit closures intersect. This is the weakest equivalence relation on the set of conjugation orbits that yields a Hausdorff space
by conjugation and two homomorphisms are defined to be equivalent if and only if their orbit closures intersect. This is the weakest equivalence relation on the set of conjugation orbits that yields a Hausdorff space
.
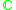 , the
, the 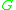 -character variety is the spectrum of prime ideals
-character variety is the spectrum of prime ideals
of the ring of invariants
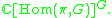
Here more generally one can consider algebraically closed fields of prime characteristic. In this generality, character varieties are only algebraic sets and are not actual varieties. To avoid technical issues, one often considers the associated reduced space by dividing by the radical of 0 (eliminating nilpotents). However, this does not necessarily yield an irrreducible space either. Moreover, if we replace the complex group by a real group we may not even get an algebraic set. In particular, a maximal compact subgroup
generally gives a semi-algebraic set. On the other hand, whenever is free we always get an honest variety; it is singular however.
is free we always get an honest variety; it is singular however.
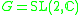 and
and  is free of rank two, then the character variety is
is free of rank two, then the character variety is 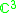 since by the Fricke-Klein-Vogt theorem its coordinate ring is isomorphic to the complex polynomial ring in 3 variables
since by the Fricke-Klein-Vogt theorem its coordinate ring is isomorphic to the complex polynomial ring in 3 variables 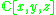 . Restricting to
. Restricting to 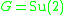 gives a closed real three dimensional ball (semi-algebraic, but not algebraic).
gives a closed real three dimensional ball (semi-algebraic, but not algebraic).
More generally, the theory of Higgs bundles implies that the (primitive) twisted character varieties of closed surface groups (genus greater than 1) are generally smooth manifolds. This is a class of examples that has been much studied.
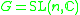 they do agree since Procesi has shown that in this case the ring of invariants is in fact generated by only traces. Since trace functions are invariant by all inner automorphisms, the Culler-Shalen construction essentially assumes that we are acting by
they do agree since Procesi has shown that in this case the ring of invariants is in fact generated by only traces. Since trace functions are invariant by all inner automorphisms, the Culler-Shalen construction essentially assumes that we are acting by
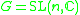
on
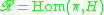
even if
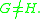
For instance, for a free group
of rank 2 and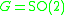 the conjugation action is trivial and the
the conjugation action is trivial and the 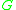 -character variety is the torus
-character variety is the torus
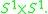
But the trace algebra is a strictly small subalgebra (there are less invariants). This provides an involutive action on the torus that needs to be accounted for to yield the Culler-Shalen character variety. The involution on this torus yields a 2-sphere. The point is that up to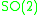 -conjugation all points are distinct, but the trace identifies elements with differing anti-diagonal elements (the involution).
-conjugation all points are distinct, but the trace identifies elements with differing anti-diagonal elements (the involution).
s, vector bundles, Higgs bundles, and geometric structures on topological spaces, given generally by the observation that, at least locally, equivalent objects in these categories are parameterized by conjugacy classes of holonomy
homomorphisms. In other words, with respect to a base space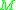 for the bundles or a fixed topological space for the geometric structures the holonomy homomorphism is a group homomorphism between
for the bundles or a fixed topological space for the geometric structures the holonomy homomorphism is a group homomorphism between 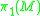 and the structure group
and the structure group 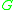 of the base space.
of the base space.
in knot theory. The skein module is roughly a deformation
(or quantization) of the character variety. This also strongly related to 3-manifold invariants.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
of moduli theory, given an algebraic, reductive, Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
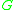 and a finitely generated group
and a finitely generated group  , the
, the 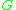 -character variety of
-character variety of  is a space of equivalence classes of group homomorphisms
is a space of equivalence classes of group homomorphisms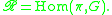
More precisely,
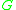 acts on
acts on 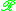 by conjugation and two homomorphisms are defined to be equivalent if and only if their orbit closures intersect. This is the weakest equivalence relation on the set of conjugation orbits that yields a Hausdorff space
by conjugation and two homomorphisms are defined to be equivalent if and only if their orbit closures intersect. This is the weakest equivalence relation on the set of conjugation orbits that yields a Hausdorff spaceHausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
.
Formulation
Formally, and when the algebraic group is defined over the complex numbers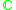 , the
, the 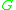 -character variety is the spectrum of prime ideals
-character variety is the spectrum of prime idealsSpectrum of a ring
In abstract algebra and algebraic geometry, the spectrum of a commutative ring R, denoted by Spec, is the set of all proper prime ideals of R...
of the ring of invariants
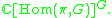
Here more generally one can consider algebraically closed fields of prime characteristic. In this generality, character varieties are only algebraic sets and are not actual varieties. To avoid technical issues, one often considers the associated reduced space by dividing by the radical of 0 (eliminating nilpotents). However, this does not necessarily yield an irrreducible space either. Moreover, if we replace the complex group by a real group we may not even get an algebraic set. In particular, a maximal compact subgroup
Maximal compact subgroup
In mathematics, a maximal compact subgroup K of a topological group G is a subgroup K that is a compact space, in the subspace topology, and maximal amongst such subgroups....
generally gives a semi-algebraic set. On the other hand, whenever
 is free we always get an honest variety; it is singular however.
is free we always get an honest variety; it is singular however.Examples
For example, if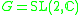 and
and  is free of rank two, then the character variety is
is free of rank two, then the character variety is 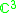 since by the Fricke-Klein-Vogt theorem its coordinate ring is isomorphic to the complex polynomial ring in 3 variables
since by the Fricke-Klein-Vogt theorem its coordinate ring is isomorphic to the complex polynomial ring in 3 variables 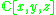 . Restricting to
. Restricting to 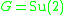 gives a closed real three dimensional ball (semi-algebraic, but not algebraic).
gives a closed real three dimensional ball (semi-algebraic, but not algebraic).More generally, the theory of Higgs bundles implies that the (primitive) twisted character varieties of closed surface groups (genus greater than 1) are generally smooth manifolds. This is a class of examples that has been much studied.
Variants
This is not necessarily the same construction as the Culler-Shalen character variety (generated by evaluations of traces), although when the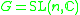 they do agree since Procesi has shown that in this case the ring of invariants is in fact generated by only traces. Since trace functions are invariant by all inner automorphisms, the Culler-Shalen construction essentially assumes that we are acting by
they do agree since Procesi has shown that in this case the ring of invariants is in fact generated by only traces. Since trace functions are invariant by all inner automorphisms, the Culler-Shalen construction essentially assumes that we are acting by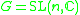
on
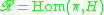
even if
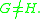
For instance, for a free group
Free group
In mathematics, a group G is called free if there is a subset S of G such that any element of G can be written in one and only one way as a product of finitely many elements of S and their inverses...
of rank 2 and
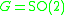 the conjugation action is trivial and the
the conjugation action is trivial and the 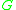 -character variety is the torus
-character variety is the torus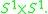
But the trace algebra is a strictly small subalgebra (there are less invariants). This provides an involutive action on the torus that needs to be accounted for to yield the Culler-Shalen character variety. The involution on this torus yields a 2-sphere. The point is that up to
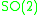 -conjugation all points are distinct, but the trace identifies elements with differing anti-diagonal elements (the involution).
-conjugation all points are distinct, but the trace identifies elements with differing anti-diagonal elements (the involution).Connection to geometry
There is an interplay between these moduli and the moduli of principal bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, vector bundles, Higgs bundles, and geometric structures on topological spaces, given generally by the observation that, at least locally, equivalent objects in these categories are parameterized by conjugacy classes of holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
homomorphisms. In other words, with respect to a base space
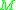 for the bundles or a fixed topological space for the geometric structures the holonomy homomorphism is a group homomorphism between
for the bundles or a fixed topological space for the geometric structures the holonomy homomorphism is a group homomorphism between 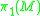 and the structure group
and the structure group 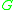 of the base space.
of the base space.Connection to skein modules
The coordinate ring of the character variety has been related to skein modulesBracket polynomial
In the mathematical field of knot theory, the bracket polynomial is a polynomial invariant of framed links. Although it is not an invariant of knots or links , a suitably "normalized" version yields the famous knot invariant called the Jones polynomial...
in knot theory. The skein module is roughly a deformation
Quantum group
In mathematics and theoretical physics, the term quantum group denotes various kinds of noncommutative algebra with additional structure. In general, a quantum group is some kind of Hopf algebra...
(or quantization) of the character variety. This also strongly related to 3-manifold invariants.

