Christofides algorithm
Encyclopedia
The goal of the Christofides heuristic algorithm
(named after Nicos Christofides) is to find a solution to the instances of the traveling salesman problem where the edge weights satisfy the triangle inequality
.
Let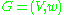
be an instance of TSP, i.e. 
is a complete graph on the set 
of vertices with weight function 
assigning a nonnegative real weight to every edge of 
.
Pseudo-code:
Step 1: Create the minimum spanning tree
MST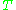
of 
.
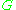Step 2: Let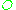
be the set of vertices with odd degree
in
and find a perfect matching 
with minimum weight in the complete graph
over the vertices from
.
Step 3: Combine the edges of
and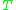 
to form a multigraph
.
Step 4: Form an Eulerian circuit in
(H is Eulerian because it is connected, with only even-degree vertices).
Step 5: Make the circuit found in previous step Hamiltonian by skipping visited nodes (shortcutting).
The proof is as follows:
Let denote the edge set of the optimal solution of TSP for . Because is connected, it contains some spanning tree and thus . Further let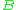
denote the edge set of the optimal solution of TSP for the complete graph over vertices from 
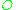. Because the edge weights are triangular (so visiting more nodes cannot reduce total cost), we know that
. We show that there is a perfect matching of vertices from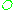
with weight under
and therefore we have the same upper bound for
(because 
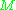is a perfect matching of minimum cost).
Because
must contain an even number of vertices, a perfect matching exists. Let
be the (only) Eulerian path in
. Clearly both
and
are perfect matchings and the weight of at least one of them is
less than or equal to .
Thus and from the triangle inequality it follows that the algorithm is 3/2-approximative.
Algorithm
In mathematics and computer science, an algorithm is an effective method expressed as a finite list of well-defined instructions for calculating a function. Algorithms are used for calculation, data processing, and automated reasoning...
(named after Nicos Christofides) is to find a solution to the instances of the traveling salesman problem where the edge weights satisfy the triangle inequality
Triangle inequality
In mathematics, the triangle inequality states that for any triangle, the sum of the lengths of any two sides must be greater than or equal to the length of the remaining side ....
.
Let
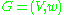be an instance of TSP, i.e. is a complete graph on the set of vertices with weight function assigning a nonnegative real weight to every edge of .Pseudo-code:
Step 1: Create the minimum spanning tree
Minimum spanning tree
Given a connected, undirected graph, a spanning tree of that graph is a subgraph that is a tree and connects all the vertices together. A single graph can have many different spanning trees...
MST
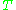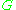of .Step 2: Let
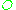be the set of vertices with odd degreeDegree (graph theory)
In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
in
and find a perfect matching with minimum weight in the complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
over the vertices from
.Step 3: Combine the edges of
and 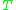to form a multigraphMultigraph
In mathematics, a multigraph or pseudograph is a graph which is permitted to have multiple edges, , that is, edges that have the same end nodes. Thus two vertices may be connected by more than one edge....
.Step 4: Form an Eulerian circuit in
(H is Eulerian because it is connected, with only even-degree vertices).Step 5: Make the circuit found in previous step Hamiltonian by skipping visited nodes (shortcutting).
Approximation ratio
The cost of the solution produced by the algorithm is within 3/2 of the optimum.The proof is as follows:
Let denote the edge set of the optimal solution of TSP for . Because is connected, it contains some spanning tree and thus . Further let
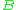denote the edge set of the optimal solution of TSP for the complete graph over vertices from 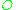. Because the edge weights are triangular (so visiting more nodes cannot reduce total cost), we know that. We show that there is a perfect matching of vertices from
with weight underand therefore we have the same upper bound for
(because is a perfect matching of minimum cost).Because
must contain an even number of vertices, a perfect matching exists. Letbe the (only) Eulerian path in
. Clearly bothand
are perfect matchings and the weight of at least one of them is
less than or equal to .
Thus and from the triangle inequality it follows that the algorithm is 3/2-approximative.