
Compound Poisson process
Encyclopedia
A compound Poisson process is a continuous-time (random) stochastic process
with jumps. The jumps arrive randomly according to a Poisson process
and the size of the jumps is also random, with a specified probability distribution. A compound Poisson process, parameterised by a rate and jump size distribution G, is a process
and jump size distribution G, is a process  given by
given by

where, is a Poisson process
is a Poisson process
with rate , and
, and 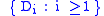 are independent and identically distributed random variables, with distribution function G, which are also independent of
are independent and identically distributed random variables, with distribution function G, which are also independent of 
, the expected value
of a compound Poisson process can be calculated as:
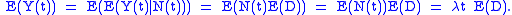
Making similar use of the law of total variance
, the variance
can be calculated as: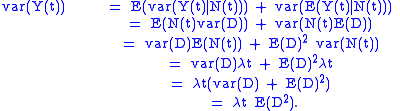
Lastly, using the law of total probability
, the moment generating function can be given as follows:
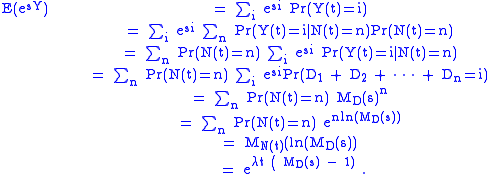
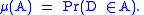
Let δ0 be the trivial probability distribution putting all of the mass at zero. Then the probability distribution
of Y(t) is the measure
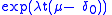
where the exponential exp(ν) of a finite measure ν on Borel subsets
of the real line
is defined by
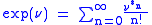
and

is a convolution
of measures, and the series converges weakly
.
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
with jumps. The jumps arrive randomly according to a Poisson process
Poisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
and the size of the jumps is also random, with a specified probability distribution. A compound Poisson process, parameterised by a rate
 and jump size distribution G, is a process
and jump size distribution G, is a process  given by
given by
where,
 is a Poisson process
is a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
with rate
 , and
, and 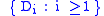 are independent and identically distributed random variables, with distribution function G, which are also independent of
are independent and identically distributed random variables, with distribution function G, which are also independent of 
Properties of the compound Poisson process
Using conditional expectationLaw of total expectation
The proposition in probability theory known as the law of total expectation, the law of iterated expectations, the tower rule, the smoothing theorem, among other names, states that if X is an integrable random variable The proposition in probability theory known as the law of total expectation, ...
, the expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
of a compound Poisson process can be calculated as:
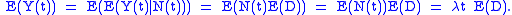
Making similar use of the law of total variance
Law of total variance
In probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...
, the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
can be calculated as:
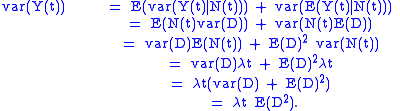
Lastly, using the law of total probability
Law of total probability
In probability theory, the law of total probability is a fundamental rule relating marginal probabilities to conditional probabilities.-Statement:The law of total probability is the proposition that if \left\...
, the moment generating function can be given as follows:
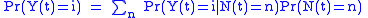
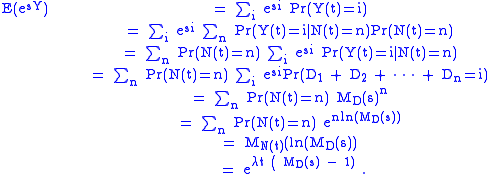
Exponentiation of measures
Let N, Y, and D be as above. Let μ be the probability measure according to which D is distributed, i.e.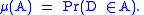
Let δ0 be the trivial probability distribution putting all of the mass at zero. Then the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of Y(t) is the measure
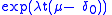
where the exponential exp(ν) of a finite measure ν on Borel subsets
Borel set
In mathematics, a Borel set is any set in a topological space that can be formed from open sets through the operations of countable union, countable intersection, and relative complement...
of the real line
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
is defined by
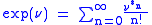
and

is a convolution
Convolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of measures, and the series converges weakly
Convergence of random variables
In probability theory, there exist several different notions of convergence of random variables. The convergence of sequences of random variables to some limit random variable is an important concept in probability theory, and its applications to statistics and stochastic processes...
.
See also
- Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
- Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
- Non-homogeneous Poisson processNon-homogeneous Poisson processIn probability theory, a non-homogeneous Poisson process is a Poisson process with rate parameter \lambda such that the rate parameter of the process is a function of time...

