Conceptual clustering
Encyclopedia
Conceptual clustering is a machine learning
paradigm for unsupervised classification developed mainly during the 1980s. It is distinguished from ordinary data clustering
by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating hierarchical category structures; see Categorization
for more information on hierarchy. Conceptual clustering is closely related to formal concept analysis
, decision tree learning
, and mixture model
learning.
which is available to the learner. Thus, a statistically strong grouping in the data may fail to be extracted by the learner if the prevailing concept description language is incapable of describing that particular regularity. In most implementations, the description language has been limited to feature conjunction
, although in COBWEB (see "COBWEB" below), the feature language is probabilistic.
More general discussions and reviews of conceptual clustering can be found in the following publications:
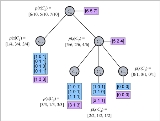
or bag) of objects, each object being represented as a binary-valued property list. The data associated with each tree node (i.e., concept) are the integer property counts for the objects in that concept. For example (see figure), let a concept
contain the following four objects (repeated objects being permitted).
The three properties might be, for example,
, the likelihood that it is male is 
. Likewise, the likelihood that the object has wings and likelihood that the object is nocturnal or both is 
. The concept description can therefore simply be given as 
-conditional feature likelihood, i.e., 
.
The figure to the right shows a concept tree with five concepts.
is the root concept, which contains all ten objects in the data set. Concepts 
and 
are the children of 
, the former containing four objects, and the later containing six objects. Concept 
is also the parent of concepts 
, 
, and 
, which contain three, two, and one object, respectively. Note that each parent node (relative superordinate concept) contains all the objects contained by its child nodes (relative subordinate concepts). In Fisher's (1987) description of COBWEB, he indicates that only the total attribute counts (not conditional probabilities, and not object lists) are stored at the nodes. Any probabilities are computed from the attribute counts as needed.
. Under this constraint, with 
, a concept such as 
. Thus, under constraints such as these, we obtain something like a traditional concept language. In the limiting case where 
for every feature, and thus every probability in a concept must be 0 or 1, the result is a feature language base on conjunction; that is, every concept that can be represented can then be described as a conjunction of features (and their negations), and concepts that cannot be described in this way cannot be represented.
(CU) measure, which he re-derives in his paper. The motivation for the measure is highly similar to the "information gain" measure introduced by Quinlan for decision tree learning. It has previously been shown that the CU for feature-based classification is the same as the mutual information
between the feature variables and the class variable (Gluck & Corter, 1985; Corter & Gluck, 1992), and since this measure is much better known, we proceed here with mutual information as the measure of category "goodness".
What we wish to evaluate is the overall utility of grouping the objects into a particular hierarchical categorization structure. Given a set of possible classification structures, we need to determine whether one is better than another.
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
paradigm for unsupervised classification developed mainly during the 1980s. It is distinguished from ordinary data clustering
Data clustering
Cluster analysis or clustering is the task of assigning a set of objects into groups so that the objects in the same cluster are more similar to each other than to those in other clusters....
by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating hierarchical category structures; see Categorization
Categorization
Categorization is the process in which ideas and objects are recognized, differentiated and understood. Categorization implies that objects are grouped into categories, usually for some specific purpose. Ideally, a category illuminates a relationship between the subjects and objects of knowledge...
for more information on hierarchy. Conceptual clustering is closely related to formal concept analysis
Formal concept analysis
Formal concept analysis is a principled way of automatically deriving an ontology from a collection of objects and their properties. The term was introduced by Rudolf Wille in 1984, and builds on applied lattice and order theory that was developed by Birkhoff and others in the 1930s.-Intuitive...
, decision tree learning
Decision tree learning
Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees...
, and mixture model
Mixture model
In statistics, a mixture model is a probabilistic model for representing the presence of sub-populations within an overall population, without requiring that an observed data-set should identify the sub-population to which an individual observation belongs...
learning.
Conceptual clustering vs. data clustering
Conceptual clustering is obviously closely related to data clustering; however, in conceptual clustering it is not only the inherent structure of the data that drives cluster formation, but also the description languageDescription language
Description language may refer to:* Interface description language aka interface definition language ** Regular Language description for XML ** Web Services Description Language ** Page description language...
which is available to the learner. Thus, a statistically strong grouping in the data may fail to be extracted by the learner if the prevailing concept description language is incapable of describing that particular regularity. In most implementations, the description language has been limited to feature conjunction
Conjunction
Conjunction can refer to:* Conjunction , an astronomical phenomenon* Astrological aspect, an aspect in horoscopic astrology* Conjunction , a part of speech** Conjunctive mood , same as subjunctive mood...
, although in COBWEB (see "COBWEB" below), the feature language is probabilistic.
List of published algorithms
A fair number of algorithms have been proposed for conceptual clustering. Some examples are given below:- CLUSTER/2 (Michalski & Stepp 1983)
- COBWEBCobweb (clustering)COBWEB is an incremental system for hierarchical conceptual clustering.COBWEB incrementally organizes observations into a classification tree. Each node in a classification tree represents a class and is labeled by a probabilistic concept that summarizes the attribute-value distributions of...
(Fisher 1987) - CYRUS (Kolodner 1983)
- GALOIS (Carpineto & Romano 1993),
- GCF (Talavera & Béjar 2001)
- INC (Hadzikadic & Yun 1989)
- ITERATE (Biswas, Weinberg & Fisher 1998),
- LABYRINTH (Thompson & Langley 1989)
- SUBDUE (Jonyer, Cook & Holder 2001).
- UNIMEM (Lebowitz 1987)
- WITT (Hanson & Bauer 1989),
More general discussions and reviews of conceptual clustering can be found in the following publications:
- Michalski (1980)
- Gennari, Langley, & Fisher (1989)
- Fisher & Pazzani (1991)
- Fisher & Langley (1986)
- Stepp & Michalski (1986)
Example: A basic conceptual clustering algorithm
This section discusses the rudiments of the conceptual clustering algorithm COBWEB. There are many other algorithms using different heuristics and "category goodness" or category evaluation criteria, but COBWEB is one of the best known. The reader is referred to the bibliography for other methods.Knowledge representation
The COBWEB data structure is a hierarchy (tree) wherein each node represents a given concept. Each concept represents a set (actually, a multisetMultiset
In mathematics, the notion of multiset is a generalization of the notion of set in which members are allowed to appear more than once...
or bag) of objects, each object being represented as a binary-valued property list. The data associated with each tree node (i.e., concept) are the integer property counts for the objects in that concept. For example (see figure), let a concept
contain the following four objects (repeated objects being permitted).[1 0 1][0 1 1][0 1 0][0 1 1]
The three properties might be, for example,
[is_male, has_wings, is_nocturnal]. Then what is stored at this concept node is the property count [1 3 3], indicating that 1 of the objects in the concept is male, 3 of the objects have wings, and 3 of the objects are nocturnal. The concept description is the category-conditional probability (likelihood) of the properties at the node. Thus, given that an object is a member of category (concept) , the likelihood that it is male is . Likewise, the likelihood that the object has wings and likelihood that the object is nocturnal or both is . The concept description can therefore simply be given as [.25 .75 .75], which corresponds to the -conditional feature likelihood, i.e., .The figure to the right shows a concept tree with five concepts.
is the root concept, which contains all ten objects in the data set. Concepts and are the children of , the former containing four objects, and the later containing six objects. Concept is also the parent of concepts , , and , which contain three, two, and one object, respectively. Note that each parent node (relative superordinate concept) contains all the objects contained by its child nodes (relative subordinate concepts). In Fisher's (1987) description of COBWEB, he indicates that only the total attribute counts (not conditional probabilities, and not object lists) are stored at the nodes. Any probabilities are computed from the attribute counts as needed.The COBWEB language
The description language of COBWEB is a "language" only in a loose sense, because being fully probabilistic it is capable of describing any concept. However, if constraints are placed on the probability ranges which concepts may represent, then a stronger language is obtained. For example, we might permit only concepts wherein at least one probability differs from 0.5 by more than. Under this constraint, with , a concept such as [.6 .5 .7] could not be constructed by the learner; however a concept such as [.6 .5 .9] would be accessible because at least one probability differs from 0.5 by more than . Thus, under constraints such as these, we obtain something like a traditional concept language. In the limiting case where for every feature, and thus every probability in a concept must be 0 or 1, the result is a feature language base on conjunction; that is, every concept that can be represented can then be described as a conjunction of features (and their negations), and concepts that cannot be described in this way cannot be represented.Evaluation criterion
In Fisher's (1987) description of COBWEB, the measure he uses to evaluate the quality of the hierarchy is Gluck and Corter's (1985) category utilityCategory utility
Category utility is a measure of "category goodness" defined in and . It was intended to supersede more limited measures of category goodness such as "cue validity" and "collocation index"...
(CU) measure, which he re-derives in his paper. The motivation for the measure is highly similar to the "information gain" measure introduced by Quinlan for decision tree learning. It has previously been shown that the CU for feature-based classification is the same as the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between the feature variables and the class variable (Gluck & Corter, 1985; Corter & Gluck, 1992), and since this measure is much better known, we proceed here with mutual information as the measure of category "goodness".
What we wish to evaluate is the overall utility of grouping the objects into a particular hierarchical categorization structure. Given a set of possible classification structures, we need to determine whether one is better than another.