Formal concept analysis
Encyclopedia
Formal concept analysis is a principled way of automatically deriving an ontology
from a collection of objects and their properties. The term was introduced by Rudolf Wille
in 1984, and builds on applied lattice and order theory
that was developed by Birkhoff and others in the 1930s.
. The approach takes as input a matrix specifying a set of objects and the properties thereof, called attributes, and finds both all the "natural" clusters of attributes and all the "natural" clusters of objects in the input data, where
Natural property clusters correspond one-for-one with natural object clusters, and a concept is a pair containing both a natural property cluster and its corresponding natural object cluster. The family of these concepts obeys the mathematical axioms defining a lattice
, and is called a concept lattice (in French this is called a Treillis de Galois because the relation between the sets of concepts and attributes is a Galois connection
).
Note the strong parallel between "natural" property clusters and definition
s in terms of individually necessary and jointly sufficient conditions, on one hand, and between "natural" object clusters and the extension
s of such definitions, on the other. Provided that the input objects and input concepts provide a complete description of the world (never true in practice, but perhaps a reasonable approximation), then the set of attributes in each concept can be interpreted as a set of singly necessary and jointly sufficient conditions for defining the set of objects in the concept. Conversely, if a set of attributes is not identified as a concept in this framework, then those attributes are not singly necessary and jointly sufficient for defining any non-empty subset of objects in the world.
 Consider O = {1,2,3,4,5,6,7,8,9,10}, and A = {composite
Consider O = {1,2,3,4,5,6,7,8,9,10}, and A = {composite
, even, odd, prime
, square
}. The smallest concept including the number 3 is the one with objects {3,5,7}, and attributes {odd, prime
}, for 3 has both of those attributes and {3,5,7} is the set of objects having that set of attributes. The largest concept involving the attribute of being square is the one with objects {1,4,9} and attributes {square
}, for 1, 4 and 9 are all the square numbers and all three of them have that set of attributes.
It can readily be seen that both of these example concepts satisfy the formal definitions below
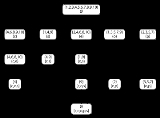
The full set of concepts for these objects and attributes is shown in the illustration. It includes a concept for each of the original attributes: the composite numbers, square numbers, even numbers, odd numbers, and prime numbers. Additionally it includes concepts for the even composite numbers, composite square numbers (that is, all square numbers except 1), even composite squares, odd squares, odd composite squares, even primes, and odd primes.
s A, and an indication of which objects have which attributes. Formally it can be regarded as a bipartite graph
I ⊆ O × A.
A (formal) concept for a context is defined to be a pair (Oi, Ai) such that
Oi is called the extent
of the concept, Ai the intent
.
A context may be described as a table, with the objects corresponding to the rows of the table, the attributes corresponding to the columns of the table, and a Boolean value (in the example represented graphically as a checkmark) in cell (x, y) whenever object x has value y:
A concept, in this representation, forms a maximal
subarray (not necessarily contiguous) such that all cells within the subarray are checked. For instance, the concept highlighted with a different background color in the example table is the one describing the odd prime numbers, and forms a 3 × 2 subarray in which all cells are checked.
Every pair of concepts in this partial order has a unique greatest lower bound (meet). The greatest lower bound of (Oi, Ai) and (Oj, Aj) is the concept with objects Oi ∩ Oj; it has as its attributes the union of Ai, Aj, and any additional attributes held by all objects in Oi ∩ Oj.
Symmetrically, every pair of concepts in this partial order has a unique least upper bound (join). The least upper bound of (Oi, Ai) and (Oj, Aj) is the concept with attributes Ai ∩ Aj; it has as its objects the union of Oi, Oj, and any additional objects that have all attributes in Ai ∩ Aj.
These meet and join operations satisfy the axioms defining a lattice
. In fact, by considering infinite meets and joins, analogously to the binary meets and joins defined above, one sees that this is a complete lattice
. It may be viewed as the Dedekind–MacNeille completion
of a partially ordered set
of height two in which the elements of the partial order are the objects and attributes of A and in which two elements x and y satisfy x ≤ y exactly when x is an object that has attribute y.
Any finite lattice may be generated as the concept lattice for some context. For, let L be a finite lattice, and form a context in which the objects and the attributes both correspond to elements of L. In this context, let object x have attribute y exactly when x and y are ordered as x ≤ y in the lattice. Then, the concept lattice of this context is isomorphic to L itself. This construction may be interpreted as forming the Dedekind–MacNeille completion of L, which is known to produce an isomorphic lattice from any finite lattice.
This can be expressed in terms of the derivative functions. The derivative of a set Oi ⊆ O of objects is the set Oi' ⊆ A of all attributes that hold for all objects in Oi. The derivative of a set Ai ⊆ A of attributes is the set Ai' ⊆ O of all objects that have all attributes in Ai. A pair (Oi, Ai) is a concept if and only if Oi' = Ai and Ai' = Oi.
Using this function, weak negation can be written asΔ = ((G\A)
and weak opposition can be written as𝛁 = ((M\B)', (M\B)
The concept lattice equipped with the two additional operations Δ and 𝛁 is known as the concept algebra of a context. Concept algebras are a generalization of power sets.
Weak negation on a concept lattice L is a weak complementation, i.e. an order-reversing map Δ: L → L which satisfies the axioms xΔΔ ≤ x and (x⋀y) ⋁ (x⋀yΔ) = x. Weak composition is a dual weak complementation. A (bounded) lattice such as a concept algebra, which is equipped with a weak complementation and a dual weak complementation, is called a weakly dicomplemented lattice. Weakly dicomplemented lattices generalize distributive orthocomplemented lattices, i.e. Boolean algebras.
of the concept lattice (also called, in formal concept analysis, a line diagram), encodes enough information to recover the original context from which it was formed. Each object of the context corresponds to a lattice element, the element with the minimal object set that contains that object, and with an attribute set consisting of all attributes of the object. Symmetrically, each attribute of the context corresponds to a lattice element, the one with the minimal attribute set containing that attribute, and with an object set consisting of all objects with that attribute. We may label the nodes of the Hasse diagram with the objects and attributes they correspond to; with this labeling, object x has attribute y if and only if there exists a monotonic path from x to y in the diagram.
of the concept lattice connects some concept C to the concept formed by the join of C with a single object. Thus, one can build up the concept lattice one concept at a time, by finding the neighbors in the Hasse diagram of known concepts, starting from the concept with an empty set of objects. The amount of time spent to traverse
the entire concept lattice in this way is polynomial in the number of input objects and attributes per generated concept.
, Coron, FcaBedrock, etc.
Ontology (computer science)
In computer science and information science, an ontology formally represents knowledge as a set of concepts within a domain, and the relationships between those concepts. It can be used to reason about the entities within that domain and may be used to describe the domain.In theory, an ontology is...
from a collection of objects and their properties. The term was introduced by Rudolf Wille
Rudolf Wille
Rudolf Wille is a German Mathematician and was Professor of General Algebra from 1970 to 2003 at Technische Universität Darmstadt...
in 1984, and builds on applied lattice and order theory
Order theory
Order theory is a branch of mathematics which investigates our intuitive notion of order using binary relations. It provides a formal framework for describing statements such as "this is less than that" or "this precedes that". This article introduces the field and gives some basic definitions...
that was developed by Birkhoff and others in the 1930s.
Intuitive description
Formal concept analysis refers to both an unsupervised machine learning technique and, more broadly, a method of data analysisData analysis
Analysis of data is a process of inspecting, cleaning, transforming, and modeling data with the goal of highlighting useful information, suggesting conclusions, and supporting decision making...
. The approach takes as input a matrix specifying a set of objects and the properties thereof, called attributes, and finds both all the "natural" clusters of attributes and all the "natural" clusters of objects in the input data, where
- a "natural" object cluster is the set of all objects that share a common subset of attributes, and
- a "natural" property cluster is the set of all attributes shared by one of the natural object clusters.
Natural property clusters correspond one-for-one with natural object clusters, and a concept is a pair containing both a natural property cluster and its corresponding natural object cluster. The family of these concepts obeys the mathematical axioms defining a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
, and is called a concept lattice (in French this is called a Treillis de Galois because the relation between the sets of concepts and attributes is a Galois connection
Galois connection
In mathematics, especially in order theory, a Galois connection is a particular correspondence between two partially ordered sets . The same notion can also be defined on preordered sets or classes; this article presents the common case of posets. Galois connections generalize the correspondence...
).
Note the strong parallel between "natural" property clusters and definition
Definition
A definition is a passage that explains the meaning of a term , or a type of thing. The term to be defined is the definiendum. A term may have many different senses or meanings...
s in terms of individually necessary and jointly sufficient conditions, on one hand, and between "natural" object clusters and the extension
Extension (semantics)
In any of several studies that treat the use of signs - for example, in linguistics, logic, mathematics, semantics, and semiotics - the extension of a concept, idea, or sign consists of the things to which it applies, in contrast with its comprehension or intension, which consists very roughly of...
s of such definitions, on the other. Provided that the input objects and input concepts provide a complete description of the world (never true in practice, but perhaps a reasonable approximation), then the set of attributes in each concept can be interpreted as a set of singly necessary and jointly sufficient conditions for defining the set of objects in the concept. Conversely, if a set of attributes is not identified as a concept in this framework, then those attributes are not singly necessary and jointly sufficient for defining any non-empty subset of objects in the world.
Example

Composite number
A composite number is a positive integer which has a positive divisor other than one or itself. In other words a composite number is any positive integer greater than one that is not a prime number....
, even, odd, prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
}. The smallest concept including the number 3 is the one with objects {3,5,7}, and attributes {odd, prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
}, for 3 has both of those attributes and {3,5,7} is the set of objects having that set of attributes. The largest concept involving the attribute of being square is the one with objects {1,4,9} and attributes {square
Square number
In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...
}, for 1, 4 and 9 are all the square numbers and all three of them have that set of attributes.
It can readily be seen that both of these example concepts satisfy the formal definitions below
The full set of concepts for these objects and attributes is shown in the illustration. It includes a concept for each of the original attributes: the composite numbers, square numbers, even numbers, odd numbers, and prime numbers. Additionally it includes concepts for the even composite numbers, composite square numbers (that is, all square numbers except 1), even composite squares, odd squares, odd composite squares, even primes, and odd primes.
Contexts and concepts
A (formal) context consists of a set of objects O, a set of attributeAttribute (computing)
In computing, an attribute is a specification that defines a property of an object, element, or file. It may also refer to or set the specific value for a given instance of such....
s A, and an indication of which objects have which attributes. Formally it can be regarded as a bipartite graph
Bipartite graph
In the mathematical field of graph theory, a bipartite graph is a graph whose vertices can be divided into two disjoint sets U and V such that every edge connects a vertex in U to one in V; that is, U and V are independent sets...
I ⊆ O × A.
| composite | even | odd | prime | square | |
|---|---|---|---|---|---|
| 1 | √ | √ | |||
| 2 | √ | √ | |||
| 3 | √ | √ | |||
| 4 | √ | √ | √ | ||
| 5 | √ | √ | |||
| 6 | √ | √ | |||
| 7 | √ | √ | |||
| 8 | √ | √ | |||
| 9 | √ | √ | √ | ||
| 10 | √ | √ |
A (formal) concept for a context is defined to be a pair (Oi, Ai) such that
- Oi ⊆ O
- Ai ⊆ A
- every object in Oi has every attribute in Ai
- for every object in O that is not in Oi, there is an attribute in Ai that the object does not have
- for every attribute in A that is not in Ai, there is an object in Oi that does not have that attribute
Oi is called the extent
Extension (semantics)
In any of several studies that treat the use of signs - for example, in linguistics, logic, mathematics, semantics, and semiotics - the extension of a concept, idea, or sign consists of the things to which it applies, in contrast with its comprehension or intension, which consists very roughly of...
of the concept, Ai the intent
Intension
In linguistics, logic, philosophy, and other fields, an intension is any property or quality connoted by a word, phrase or other symbol. In the case of a word, it is often implied by the word's definition...
.
A context may be described as a table, with the objects corresponding to the rows of the table, the attributes corresponding to the columns of the table, and a Boolean value (in the example represented graphically as a checkmark) in cell (x, y) whenever object x has value y:
A concept, in this representation, forms a maximal
Maximal
Maximal may refer to:*Maximal element, a mathematical definition*Maximal , a faction of Transformers*Maximalism, an artistic style*Maximal set*Maxim , a men's magazine marketed as Maximal in several countriesSee also...
subarray (not necessarily contiguous) such that all cells within the subarray are checked. For instance, the concept highlighted with a different background color in the example table is the one describing the odd prime numbers, and forms a 3 × 2 subarray in which all cells are checked.
Concept lattice of a context
The concepts (Oi, Ai) defined above can be partially ordered by inclusion: if (Oi, Ai) and (Oj, Aj) are concepts, we define a partial order ≤ by saying that (Oi, Ai) ≤ (Oj, Aj) whenever Oi ⊆ Oj. Equivalently, (Oi, Ai) ≤ (Oj, Aj) whenever Aj ⊆ Ai.Every pair of concepts in this partial order has a unique greatest lower bound (meet). The greatest lower bound of (Oi, Ai) and (Oj, Aj) is the concept with objects Oi ∩ Oj; it has as its attributes the union of Ai, Aj, and any additional attributes held by all objects in Oi ∩ Oj.
Symmetrically, every pair of concepts in this partial order has a unique least upper bound (join). The least upper bound of (Oi, Ai) and (Oj, Aj) is the concept with attributes Ai ∩ Aj; it has as its objects the union of Oi, Oj, and any additional objects that have all attributes in Ai ∩ Aj.
These meet and join operations satisfy the axioms defining a lattice
Lattice (order)
In mathematics, a lattice is a partially ordered set in which any two elements have a unique supremum and an infimum . Lattices can also be characterized as algebraic structures satisfying certain axiomatic identities...
. In fact, by considering infinite meets and joins, analogously to the binary meets and joins defined above, one sees that this is a complete lattice
Complete lattice
In mathematics, a complete lattice is a partially ordered set in which all subsets have both a supremum and an infimum . Complete lattices appear in many applications in mathematics and computer science...
. It may be viewed as the Dedekind–MacNeille completion
Dedekind–MacNeille completion
In order-theoretic mathematics, the Dedekind–MacNeille completion of a partially ordered set is the smallest complete lattice that contains the given partial order...
of a partially ordered set
Partially ordered set
In mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
of height two in which the elements of the partial order are the objects and attributes of A and in which two elements x and y satisfy x ≤ y exactly when x is an object that has attribute y.
Any finite lattice may be generated as the concept lattice for some context. For, let L be a finite lattice, and form a context in which the objects and the attributes both correspond to elements of L. In this context, let object x have attribute y exactly when x and y are ordered as x ≤ y in the lattice. Then, the concept lattice of this context is isomorphic to L itself. This construction may be interpreted as forming the Dedekind–MacNeille completion of L, which is known to produce an isomorphic lattice from any finite lattice.
Concept algebra of a context
Modelling negation in a formal context is somewhat problematic because the complement (O\Oi, A\Ai) of a concept (Oi, Ai) is in general not a concept. However, since the concept lattice is complete one can consider the join (Oi, Ai)Δ of all concepts (Oj, Aj) that satisfy Oj ⊆ G\Oi; or dually the meet (Oi, Ai)𝛁 of all concepts satisfying Aj ⊆ G\Ai. These two operations are known as weak negation and weak opposition, respectively.This can be expressed in terms of the derivative functions. The derivative of a set Oi ⊆ O of objects is the set Oi' ⊆ A of all attributes that hold for all objects in Oi. The derivative of a set Ai ⊆ A of attributes is the set Ai' ⊆ O of all objects that have all attributes in Ai. A pair (Oi, Ai) is a concept if and only if Oi' = Ai and Ai' = Oi.
Using this function, weak negation can be written asΔ = ((G\A)
and weak opposition can be written as𝛁 = ((M\B)', (M\B)
The concept lattice equipped with the two additional operations Δ and 𝛁 is known as the concept algebra of a context. Concept algebras are a generalization of power sets.
Weak negation on a concept lattice L is a weak complementation, i.e. an order-reversing map Δ: L → L which satisfies the axioms xΔΔ ≤ x and (x⋀y) ⋁ (x⋀yΔ) = x. Weak composition is a dual weak complementation. A (bounded) lattice such as a concept algebra, which is equipped with a weak complementation and a dual weak complementation, is called a weakly dicomplemented lattice. Weakly dicomplemented lattices generalize distributive orthocomplemented lattices, i.e. Boolean algebras.
Recovering the context from the Hasse diagram
The Hasse diagramHasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
of the concept lattice (also called, in formal concept analysis, a line diagram), encodes enough information to recover the original context from which it was formed. Each object of the context corresponds to a lattice element, the element with the minimal object set that contains that object, and with an attribute set consisting of all attributes of the object. Symmetrically, each attribute of the context corresponds to a lattice element, the one with the minimal attribute set containing that attribute, and with an object set consisting of all objects with that attribute. We may label the nodes of the Hasse diagram with the objects and attributes they correspond to; with this labeling, object x has attribute y if and only if there exists a monotonic path from x to y in the diagram.
Efficient construction
survey the many algorithms that have been developed for constructing concept lattices. These algorithms vary in many details, but are in general based on the idea that each edge of the Hasse diagramHasse diagram
In order theory, a branch of mathematics, a Hasse diagram is a type of mathematical diagram used to represent a finite partially ordered set, in the form of a drawing of its transitive reduction...
of the concept lattice connects some concept C to the concept formed by the join of C with a single object. Thus, one can build up the concept lattice one concept at a time, by finding the neighbors in the Hasse diagram of known concepts, starting from the concept with an empty set of objects. The amount of time spent to traverse
Graph traversal
Graph traversal refers to the problem of visiting all the nodes in a graph in a particular manner. Tree traversal is a special case of graph traversal...
the entire concept lattice in this way is polynomial in the number of input objects and attributes per generated concept.
Formal Concept Analysis tools
Many FCA software applications are available today. The main purpose of these tools varies from formal context creation to formal concept mining and generating the concepts lattice of a given formal context and the corresponding association rules. Most of these tools are academic and still under active development. One can find a non exhaustive list of FCA tools in the FCA software website. Most of these tools are open-source applications like ConExp, ToscanaJ, Lattice MinerLattice Miner
Lattice Miner is a formal concept analysis software tool for the construction, visualization and manipulation of concept lattices. It allows the generation of formal concepts and association rules as well as the transformation of formal contexts via apposition, subposition, reduction and...
, Coron, FcaBedrock, etc.
See also
- BiclusteringBiclusteringBiclustering, co-clustering, or two-mode clustering is a data mining technique which allows simultaneous clustering of the rows and columns of a matrix....
- Cluster analysis
- Concept miningConcept MiningConcept mining is an activity that results in the extraction of concepts from artifacts. Solutions to the task typically involve aspects of artificial intelligence and statistics, such as data mining and text mining...
- Conceptual clusteringConceptual clusteringConceptual clustering is a machine learning paradigm for unsupervised classification developed mainly during the 1980s. It is distinguished from ordinary data clustering by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating...

