
Category utility
Encyclopedia
Category utility is a measure of "category goodness" defined in and . It was intended to supersede more limited measures of category goodness such as "cue validity
" and "collocation index" . It provides a normative information-theoretic measure of the predictive advantage gained by the observer who possesses knowledge of the given category structure (i.e., the class labels of instances) over the observer who does not possess knowledge of the category structure. In this sense the motivation for the category utility measure is similar to the information gain
metric used in decision tree
learning. In certain presentations, it is also formally equivalent to the mutual information
, as discussed below. A review of category utility in its probabilistic incarnation, with applications to machine learning
, is provided in .
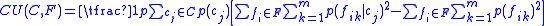
where is a size-
is a size-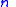 set of
set of  -ary features, and
-ary features, and  is a set of
is a set of  categories. The term
categories. The term 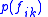 designates the marginal probability that feature
designates the marginal probability that feature 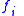 takes on value
takes on value  , and the term
, and the term  designates the category-conditional probability
designates the category-conditional probability
that feature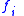 takes on value
takes on value  given that the object in question belongs to category
given that the object in question belongs to category 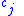 .
.
The motivation and development of this expression for category utility, and the role of the multiplicand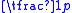 as a crude overfitting control, is given in the above sources. Loosely , the term
as a crude overfitting control, is given in the above sources. Loosely , the term 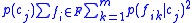 is the expected number of attribute values that can be correctly guessed by an observer using a probability-matching strategy together with knowledge of the category labels, while
is the expected number of attribute values that can be correctly guessed by an observer using a probability-matching strategy together with knowledge of the category labels, while 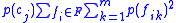 is the expected number of attribute values that can be correctly guessed by an observer the same strategy but without any knowledge of the category labels. Their difference therefore reflects the relative advantage accruing to the observer by having knowledge of the category structure.
is the expected number of attribute values that can be correctly guessed by an observer the same strategy but without any knowledge of the category labels. Their difference therefore reflects the relative advantage accruing to the observer by having knowledge of the category structure.
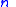 binary feature set
binary feature set 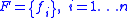 , and a binary category
, and a binary category 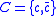 is given in as follows:
is given in as follows:
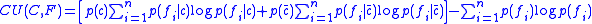
where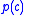 is the prior probability
is the prior probability
of an entity belonging to the positive category (in the absence of any feature information),
(in the absence of any feature information), 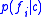 is the conditional probability
is the conditional probability
of an entity having feature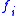 given that the entity belongs to category
given that the entity belongs to category  ,
, 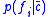 is likewise the conditional probability of an entity having feature
is likewise the conditional probability of an entity having feature  given that the entity belongs to category
given that the entity belongs to category 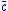 , and
, and  is the prior probability of an entity possessing feature
is the prior probability of an entity possessing feature 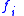 (in the absence of any category information).
(in the absence of any category information).
The intuition behind the above expression is as follows: The term represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category
represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category  . Similarly, the term
. Similarly, the term 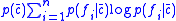 represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category
represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category  . The sum of these two terms in the brackets is therefore the weighted average of these two costs. The final term,
. The sum of these two terms in the brackets is therefore the weighted average of these two costs. The final term, 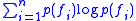 , represents the cost (in bits) of optimally encoding (or transmitting) feature information when no category information is available. The value of the category utility will, in the above formulation, be negative (???).
, represents the cost (in bits) of optimally encoding (or transmitting) feature information when no category information is available. The value of the category utility will, in the above formulation, be negative (???).
. Here we provide a simple demonstration of the nature of this equivalence. Let us assume a set of entities each having the same features, i.e., feature set
features, i.e., feature set 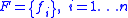 , with each feature variable having cardinality
, with each feature variable having cardinality  . That is, each feature has the capacity to adopt any of
. That is, each feature has the capacity to adopt any of  distinct values (which need not be ordered; all variables can be nominal); for the special case
distinct values (which need not be ordered; all variables can be nominal); for the special case 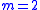 these features would be considered binary, but more generally, for any
these features would be considered binary, but more generally, for any  , the features are simply m-ary. For our purposes, without loss of generality, we can replace feature set
, the features are simply m-ary. For our purposes, without loss of generality, we can replace feature set  with a single aggregate variable
with a single aggregate variable 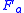 that has cardinality
that has cardinality 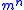 , and adopts a unique value
, and adopts a unique value  corresponding to each feature combination in the Cartesian product
corresponding to each feature combination in the Cartesian product
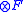 . (Ordinality does not matter, because the mutual information is not sensitive to ordinality.) In what follows, a term such as
. (Ordinality does not matter, because the mutual information is not sensitive to ordinality.) In what follows, a term such as 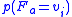 or simply
or simply  refers to the probability
refers to the probability
with which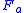 adopts the particular value
adopts the particular value 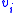 . (Using the aggregate feature variable
. (Using the aggregate feature variable 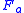 replaces multiple summations, and simplifies the presentation to follow.)
replaces multiple summations, and simplifies the presentation to follow.)
We assume also a single category variable , which has cardinality
, which has cardinality  . This is equivalent to a classification system in which there are
. This is equivalent to a classification system in which there are  non-intersecting categories. In the special case of
non-intersecting categories. In the special case of  we have the two-category case discussed above. From the definition of mutual information
we have the two-category case discussed above. From the definition of mutual information
for discrete variables, the mutual information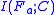 between the aggregate feature variable
between the aggregate feature variable 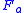 and the category variable
and the category variable  is given by:
is given by:
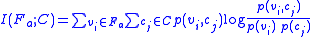
where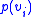 is the prior probability
is the prior probability
of feature variable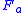 adopting value
adopting value 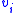 ,
, 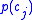 is the marginal probability of category variable
is the marginal probability of category variable  adopting value
adopting value 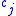 , and
, and 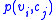 is the joint probability of variables
is the joint probability of variables 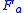 and
and  simultaneously adopting those respective values. In terms of the conditional probabilities this can be re-written (or defined) as
simultaneously adopting those respective values. In terms of the conditional probabilities this can be re-written (or defined) as
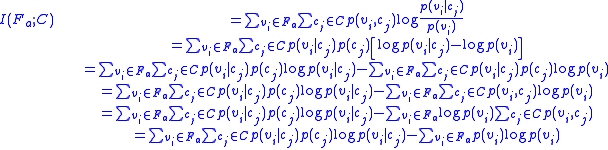
If we will rewrite the original definition of the category utility from above, with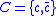 , we have
, we have

This equation clearly has the same form as the (blue) equation expressing the mutual information between the feature set and the category variable; the difference is that the sum in the category utility equation runs over independent binary variables
in the category utility equation runs over independent binary variables  , whereas the sum
, whereas the sum  in the mutual information runs over values of the single
in the mutual information runs over values of the single  -ary variable
-ary variable 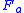 . The two measures are actually equivalent then only when the features
. The two measures are actually equivalent then only when the features 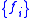 , are independent (and assuming that terms in the sum corresponding to
, are independent (and assuming that terms in the sum corresponding to  are also added).
are also added).
, the category utility is not sensitive to any ordering in the feature or category variable values. That is, as far as the category utility is concerned, the category set
aspects of "category goodness" that might be based on such ordering effects. One possible adjustment for this insensitivity to ordinality is given by the weighting scheme described in the article for mutual information
.
there has been a tremendous fascination in philosophy with the nature of concepts and universals. What kind of entity is a concept such as "horse"? Such abstractions do not designate any particular individual in the world, and yet we can scarcely imagine being able to comprehend the world without their use. Does the concept "horse" therefore have an independent existence outside of the mind? If it does, then what is the locus of this independent existence? The question of locus was an important issue on which the classical schools of Plato
and Aristotle
famously differed. However, they remained in agreement that universals did indeed have a mind-independent existence. There was, therefore, always a fact to the matter about which concepts and universals exist in the world.
In the late Middle Ages
(perhaps beginning with Occam
, although Porphyry
also makes a much earlier remark indicating a certain discomfort with the status quo), however, the certainty that existed on this issue began to erode, and it became acceptable among the so-called nominalists and empiricists to consider concepts and universals as strictly mental entities or conventions of language. On this view of concepts—that they are purely representational constructs—a new question then comes to the fore: Why do we possess one set of concepts rather than another? What makes one set of concepts "good" and another set of concepts "bad"? This is a question that modern philosophers, and subsequently machine learning
theorists and cognitive scientists, have struggled with for many decades.
: By imposing a particular categorization on the universe, an organism gains the ability to deal with physically non-identical objects or situations in an identical fashion, thereby gaining substantial predictive leverage . As J.S. Mill puts it ,
From this base, Mill reaches the following conclusion, which foreshadows much subsequent thinking about category goodness, including the notion of category utility:
One may compare this to the "category utility hypothesis" proposed by : "A category is useful to the extent that it can be expected to improve the ability of a person to accurately predict the features of instances of that category." Mill here seems to be suggesting that the best category structure is one in which object features (properties) are maximally informative about the object's class, and, simultaneously, the object class is maximally informative about the object's features. In other words, a useful classification scheme is one in which we can use category knowledge to accurately infer object properties, and we can use property knowledge to accurately infer object classes. One may also compare this idea to Aristotle
's criterion of counter-predication for definitional predicates, as well as to the notion of concepts described in formal concept analysis
.
". Cue validity of a feature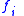 with respect to category
with respect to category 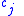 is defined as the conditional probability of the category given the feature ,
is defined as the conditional probability of the category given the feature , 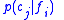 , or as the deviation of the conditional probability from the category base rate ,
, or as the deviation of the conditional probability from the category base rate , 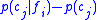 . Clearly, these measures quantify only inference from feature to category (i.e., cue validity), but not from category to feature, i.e., the category validity
. Clearly, these measures quantify only inference from feature to category (i.e., cue validity), but not from category to feature, i.e., the category validity 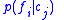 . Also, while the cue validity was originally intended to account for the demonstrable appearance of basic categories in human cognition—categories of a particular level of generality that are evidently preferred by human learners—a number of major flaws in the cue validity quickly emerged in this regard .
. Also, while the cue validity was originally intended to account for the demonstrable appearance of basic categories in human cognition—categories of a particular level of generality that are evidently preferred by human learners—a number of major flaws in the cue validity quickly emerged in this regard .
One attempt to address both problems by simultaneously maximizing both feature validity and category validity was made by in defining the "collocation index" as the product , but this construction was fairly ad hoc (see ). The category utility was introduced as a more sophisticated refinement of the cue validity, which attempts to more rigorously quantify the full inferential power of a class structure. As shown above, on a certain view the category utility is equivalent to the mutual information
, but this construction was fairly ad hoc (see ). The category utility was introduced as a more sophisticated refinement of the cue validity, which attempts to more rigorously quantify the full inferential power of a class structure. As shown above, on a certain view the category utility is equivalent to the mutual information
between the feature variable and the category variable. It has been suggested that categories having the greatest overall category utility are those that are not only those "best" in a normative sense, but also those human learners prefer to use, e.g., "basic" categories . Other related measures of category goodness are "cohesion" and "salience" .
, Abstraction
, Universals, Conceptual Clustering
, Unsupervised learning
Cue validity
Cue validity is the conditional probability that an object falls in a particular category given a particular feature or cue. The term was popularized by , and especially by Eleanor Rosch in her investigations of the acquisition of so-called basic categories .-Definition of cue validity:Formally,...
" and "collocation index" . It provides a normative information-theoretic measure of the predictive advantage gained by the observer who possesses knowledge of the given category structure (i.e., the class labels of instances) over the observer who does not possess knowledge of the category structure. In this sense the motivation for the category utility measure is similar to the information gain
Information gain in decision trees
In information theory and machine learning, information gain is an alternative synonym for Kullback–Leibler divergence.In particular, the information gain about a random variable X obtained from an observation that a random variable A takes the value A=a is the Kullback-Leibler divergence DKL of...
metric used in decision tree
Decision tree
A decision tree is a decision support tool that uses a tree-like graph or model of decisions and their possible consequences, including chance event outcomes, resource costs, and utility. It is one way to display an algorithm. Decision trees are commonly used in operations research, specifically...
learning. In certain presentations, it is also formally equivalent to the mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, as discussed below. A review of category utility in its probabilistic incarnation, with applications to machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
, is provided in .
Probability-theoretic definition of the Category Utility
The probability-theoretic definition of category utility given in and is as follows: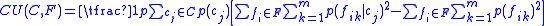
where
 is a size-
is a size-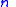 set of
set of  -ary features, and
-ary features, and  is a set of
is a set of  categories. The term
categories. The term 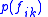 designates the marginal probability that feature
designates the marginal probability that feature 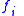 takes on value
takes on value  , and the term
, and the term  designates the category-conditional probability
designates the category-conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
that feature
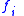 takes on value
takes on value  given that the object in question belongs to category
given that the object in question belongs to category 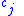 .
.The motivation and development of this expression for category utility, and the role of the multiplicand
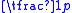 as a crude overfitting control, is given in the above sources. Loosely , the term
as a crude overfitting control, is given in the above sources. Loosely , the term 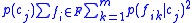 is the expected number of attribute values that can be correctly guessed by an observer using a probability-matching strategy together with knowledge of the category labels, while
is the expected number of attribute values that can be correctly guessed by an observer using a probability-matching strategy together with knowledge of the category labels, while 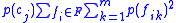 is the expected number of attribute values that can be correctly guessed by an observer the same strategy but without any knowledge of the category labels. Their difference therefore reflects the relative advantage accruing to the observer by having knowledge of the category structure.
is the expected number of attribute values that can be correctly guessed by an observer the same strategy but without any knowledge of the category labels. Their difference therefore reflects the relative advantage accruing to the observer by having knowledge of the category structure.Information-theoretic definition of the Category Utility
The information-theoretic definition of category utility for a set of entities with size-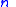 binary feature set
binary feature set 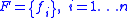 , and a binary category
, and a binary category 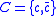 is given in as follows:
is given in as follows: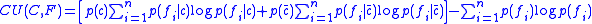
where
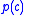 is the prior probability
is the prior probabilityPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
of an entity belonging to the positive category
 (in the absence of any feature information),
(in the absence of any feature information), 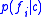 is the conditional probability
is the conditional probabilityConditional probability
In probability theory, the "conditional probability of A given B" is the probability of A if B is known to occur. It is commonly notated P, and sometimes P_B. P can be visualised as the probability of event A when the sample space is restricted to event B...
of an entity having feature
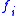 given that the entity belongs to category
given that the entity belongs to category  ,
, 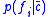 is likewise the conditional probability of an entity having feature
is likewise the conditional probability of an entity having feature  given that the entity belongs to category
given that the entity belongs to category 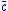 , and
, and  is the prior probability of an entity possessing feature
is the prior probability of an entity possessing feature 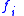 (in the absence of any category information).
(in the absence of any category information).The intuition behind the above expression is as follows: The term
 represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category
represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category  . Similarly, the term
. Similarly, the term 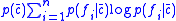 represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category
represents the cost (in bits) of optimally encoding (or transmitting) feature information when it known that the objects to be described belong to category  . The sum of these two terms in the brackets is therefore the weighted average of these two costs. The final term,
. The sum of these two terms in the brackets is therefore the weighted average of these two costs. The final term, 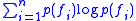 , represents the cost (in bits) of optimally encoding (or transmitting) feature information when no category information is available. The value of the category utility will, in the above formulation, be negative (???).
, represents the cost (in bits) of optimally encoding (or transmitting) feature information when no category information is available. The value of the category utility will, in the above formulation, be negative (???).Category Utility and Mutual Information
It is mentioned in and that the category utility is equivalent to the mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
. Here we provide a simple demonstration of the nature of this equivalence. Let us assume a set of entities each having the same
 features, i.e., feature set
features, i.e., feature set 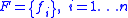 , with each feature variable having cardinality
, with each feature variable having cardinality  . That is, each feature has the capacity to adopt any of
. That is, each feature has the capacity to adopt any of  distinct values (which need not be ordered; all variables can be nominal); for the special case
distinct values (which need not be ordered; all variables can be nominal); for the special case 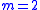 these features would be considered binary, but more generally, for any
these features would be considered binary, but more generally, for any  , the features are simply m-ary. For our purposes, without loss of generality, we can replace feature set
, the features are simply m-ary. For our purposes, without loss of generality, we can replace feature set  with a single aggregate variable
with a single aggregate variable 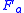 that has cardinality
that has cardinality 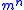 , and adopts a unique value
, and adopts a unique value  corresponding to each feature combination in the Cartesian product
corresponding to each feature combination in the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
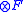 . (Ordinality does not matter, because the mutual information is not sensitive to ordinality.) In what follows, a term such as
. (Ordinality does not matter, because the mutual information is not sensitive to ordinality.) In what follows, a term such as 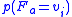 or simply
or simply  refers to the probability
refers to the probabilityProbability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
with which
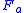 adopts the particular value
adopts the particular value 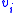 . (Using the aggregate feature variable
. (Using the aggregate feature variable 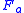 replaces multiple summations, and simplifies the presentation to follow.)
replaces multiple summations, and simplifies the presentation to follow.)We assume also a single category variable
 , which has cardinality
, which has cardinality  . This is equivalent to a classification system in which there are
. This is equivalent to a classification system in which there are  non-intersecting categories. In the special case of
non-intersecting categories. In the special case of  we have the two-category case discussed above. From the definition of mutual information
we have the two-category case discussed above. From the definition of mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
for discrete variables, the mutual information
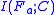 between the aggregate feature variable
between the aggregate feature variable 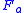 and the category variable
and the category variable  is given by:
is given by: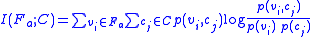
where
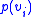 is the prior probability
is the prior probabilityPrior probability
In Bayesian statistical inference, a prior probability distribution, often called simply the prior, of an uncertain quantity p is the probability distribution that would express one's uncertainty about p before the "data"...
of feature variable
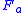 adopting value
adopting value 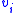 ,
, 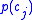 is the marginal probability of category variable
is the marginal probability of category variable  adopting value
adopting value 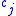 , and
, and 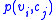 is the joint probability of variables
is the joint probability of variables 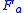 and
and  simultaneously adopting those respective values. In terms of the conditional probabilities this can be re-written (or defined) as
simultaneously adopting those respective values. In terms of the conditional probabilities this can be re-written (or defined) as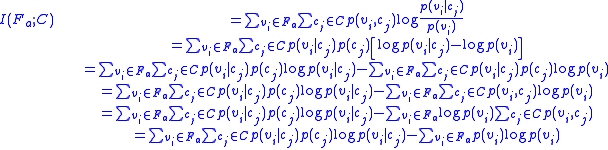
If we will rewrite the original definition of the category utility from above, with
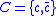 , we have
, we have
This equation clearly has the same form as the (blue) equation expressing the mutual information between the feature set and the category variable; the difference is that the sum
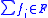 in the category utility equation runs over independent binary variables
in the category utility equation runs over independent binary variables 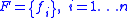 , whereas the sum
, whereas the sum  in the mutual information runs over values of the single
in the mutual information runs over values of the single  -ary variable
-ary variable 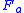 . The two measures are actually equivalent then only when the features
. The two measures are actually equivalent then only when the features 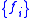 , are independent (and assuming that terms in the sum corresponding to
, are independent (and assuming that terms in the sum corresponding to  are also added).
are also added).Insensitivity of category utility to ordinality
Like the mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
, the category utility is not sensitive to any ordering in the feature or category variable values. That is, as far as the category utility is concerned, the category set
{small,medium,large,jumbo} is not qualitatively different than the category set {desk,fish,tree,mop} since the formulation of the category utility does not account for any ordering of the class variable. Similarly, a feature variable adopting values {1,2,3,4,5} is not qualitatively different from a feature variable adopting values {fred,joe,bob,sue,elaine}. As far as the category utility or mutual information are concerned, all category and feature variables are nominal variables. For this reason, category utility does not reflect any gestaltGestalt psychology
Gestalt psychology or gestaltism is a theory of mind and brain of the Berlin School; the operational principle of gestalt psychology is that the brain is holistic, parallel, and analog, with self-organizing tendencies...
aspects of "category goodness" that might be based on such ordering effects. One possible adjustment for this insensitivity to ordinality is given by the weighting scheme described in the article for mutual information
Mutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
.
Category "goodness": Models and Philosophy
This section provides some background on the origins of, and need for, formal measures of "category goodness" such as the category utility, and some of the history that lead to the development of this particular metric.What makes a good category?
At least since the time of AristotleAristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
there has been a tremendous fascination in philosophy with the nature of concepts and universals. What kind of entity is a concept such as "horse"? Such abstractions do not designate any particular individual in the world, and yet we can scarcely imagine being able to comprehend the world without their use. Does the concept "horse" therefore have an independent existence outside of the mind? If it does, then what is the locus of this independent existence? The question of locus was an important issue on which the classical schools of Plato
Plato
Plato , was a Classical Greek philosopher, mathematician, student of Socrates, writer of philosophical dialogues, and founder of the Academy in Athens, the first institution of higher learning in the Western world. Along with his mentor, Socrates, and his student, Aristotle, Plato helped to lay the...
and Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
famously differed. However, they remained in agreement that universals did indeed have a mind-independent existence. There was, therefore, always a fact to the matter about which concepts and universals exist in the world.
In the late Middle Ages
Middle Ages
The Middle Ages is a periodization of European history from the 5th century to the 15th century. The Middle Ages follows the fall of the Western Roman Empire in 476 and precedes the Early Modern Era. It is the middle period of a three-period division of Western history: Classic, Medieval and Modern...
(perhaps beginning with Occam
William of Ockham
William of Ockham was an English Franciscan friar and scholastic philosopher, who is believed to have been born in Ockham, a small village in Surrey. He is considered to be one of the major figures of medieval thought and was at the centre of the major intellectual and political controversies of...
, although Porphyry
Porphyry (philosopher)
Porphyry of Tyre , Porphyrios, AD 234–c. 305) was a Neoplatonic philosopher who was born in Tyre. He edited and published the Enneads, the only collection of the work of his teacher Plotinus. He also wrote many works himself on a wide variety of topics...
also makes a much earlier remark indicating a certain discomfort with the status quo), however, the certainty that existed on this issue began to erode, and it became acceptable among the so-called nominalists and empiricists to consider concepts and universals as strictly mental entities or conventions of language. On this view of concepts—that they are purely representational constructs—a new question then comes to the fore: Why do we possess one set of concepts rather than another? What makes one set of concepts "good" and another set of concepts "bad"? This is a question that modern philosophers, and subsequently machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
theorists and cognitive scientists, have struggled with for many decades.
What purpose do concepts serve?
One approach to answering such questions is to investigate the "role" or "purpose" of concepts in cognition. Thus, we ask: What are concepts good for in the first place? The answer provided by and many others is that classification (conception) is a precursor to inductionInductive reasoning
Inductive reasoning, also known as induction or inductive logic, is a kind of reasoning that constructs or evaluates propositions that are abstractions of observations. It is commonly construed as a form of reasoning that makes generalizations based on individual instances...
: By imposing a particular categorization on the universe, an organism gains the ability to deal with physically non-identical objects or situations in an identical fashion, thereby gaining substantial predictive leverage . As J.S. Mill puts it ,
From this base, Mill reaches the following conclusion, which foreshadows much subsequent thinking about category goodness, including the notion of category utility:
One may compare this to the "category utility hypothesis" proposed by : "A category is useful to the extent that it can be expected to improve the ability of a person to accurately predict the features of instances of that category." Mill here seems to be suggesting that the best category structure is one in which object features (properties) are maximally informative about the object's class, and, simultaneously, the object class is maximally informative about the object's features. In other words, a useful classification scheme is one in which we can use category knowledge to accurately infer object properties, and we can use property knowledge to accurately infer object classes. One may also compare this idea to Aristotle
Aristotle
Aristotle was a Greek philosopher and polymath, a student of Plato and teacher of Alexander the Great. His writings cover many subjects, including physics, metaphysics, poetry, theater, music, logic, rhetoric, linguistics, politics, government, ethics, biology, and zoology...
's criterion of counter-predication for definitional predicates, as well as to the notion of concepts described in formal concept analysis
Formal concept analysis
Formal concept analysis is a principled way of automatically deriving an ontology from a collection of objects and their properties. The term was introduced by Rudolf Wille in 1984, and builds on applied lattice and order theory that was developed by Birkhoff and others in the 1930s.-Intuitive...
.
Attempts at formalization
A variety of different measures have been suggested with an aim of formally capturing this notion of "category goodness," the best known of which is probably the "cue validityCue validity
Cue validity is the conditional probability that an object falls in a particular category given a particular feature or cue. The term was popularized by , and especially by Eleanor Rosch in her investigations of the acquisition of so-called basic categories .-Definition of cue validity:Formally,...
". Cue validity of a feature
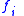 with respect to category
with respect to category 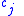 is defined as the conditional probability of the category given the feature ,
is defined as the conditional probability of the category given the feature , 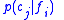 , or as the deviation of the conditional probability from the category base rate ,
, or as the deviation of the conditional probability from the category base rate , 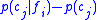 . Clearly, these measures quantify only inference from feature to category (i.e., cue validity), but not from category to feature, i.e., the category validity
. Clearly, these measures quantify only inference from feature to category (i.e., cue validity), but not from category to feature, i.e., the category validity 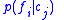 . Also, while the cue validity was originally intended to account for the demonstrable appearance of basic categories in human cognition—categories of a particular level of generality that are evidently preferred by human learners—a number of major flaws in the cue validity quickly emerged in this regard .
. Also, while the cue validity was originally intended to account for the demonstrable appearance of basic categories in human cognition—categories of a particular level of generality that are evidently preferred by human learners—a number of major flaws in the cue validity quickly emerged in this regard .One attempt to address both problems by simultaneously maximizing both feature validity and category validity was made by in defining the "collocation index" as the product
 , but this construction was fairly ad hoc (see ). The category utility was introduced as a more sophisticated refinement of the cue validity, which attempts to more rigorously quantify the full inferential power of a class structure. As shown above, on a certain view the category utility is equivalent to the mutual information
, but this construction was fairly ad hoc (see ). The category utility was introduced as a more sophisticated refinement of the cue validity, which attempts to more rigorously quantify the full inferential power of a class structure. As shown above, on a certain view the category utility is equivalent to the mutual informationMutual information
In probability theory and information theory, the mutual information of two random variables is a quantity that measures the mutual dependence of the two random variables...
between the feature variable and the category variable. It has been suggested that categories having the greatest overall category utility are those that are not only those "best" in a normative sense, but also those human learners prefer to use, e.g., "basic" categories . Other related measures of category goodness are "cohesion" and "salience" .
Applications
- Category utilility is used as the category evaluation measure in the popular conceptual clusteringConceptual clusteringConceptual clustering is a machine learning paradigm for unsupervised classification developed mainly during the 1980s. It is distinguished from ordinary data clustering by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating...
algorithm called COBWEB .
See also
Concepts, Concept learningConcept learning
Concept learning, also known as category learning, concept attainment, and concept formation, is largely based on the works of the cognitive psychologist Jerome Bruner...
, Abstraction
Abstraction
Abstraction is a process by which higher concepts are derived from the usage and classification of literal concepts, first principles, or other methods....
, Universals, Conceptual Clustering
Conceptual clustering
Conceptual clustering is a machine learning paradigm for unsupervised classification developed mainly during the 1980s. It is distinguished from ordinary data clustering by generating a concept description for each generated class. Most conceptual clustering methods are capable of generating...
, Unsupervised learning
Unsupervised learning
In machine learning, unsupervised learning refers to the problem of trying to find hidden structure in unlabeled data. Since the examples given to the learner are unlabeled, there is no error or reward signal to evaluate a potential solution...

