Conditional random field
Encyclopedia
A conditional random field (CRF) is a statistical modelling method
often applied in pattern recognition
.
More specifically it is a type of discriminative
undirected probabilistic
graphical model
. It is used to encode known relationships between observations and construct consistent interpretations. It is often used for labeling
or parsing
of sequential data, such as natural language text
or biological sequences
and in computer vision
. Specifically, CRFs find applications in shallow parsing
, named entity recognition
and gene finding
, among other tasks, being an alternative to the related hidden Markov model
s. In computer vision, CRFs are often used for object recognition and image segmentation.
and random variables 
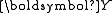as follows:
What this means is that a CRF is an undirected graphical model
whose nodes can be divided into exactly two disjoint sets
and 
, the observed and output variables, respectively; the conditional distribution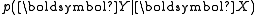 
is then modeled.
However there exist special cases for which exact inference is feasible:
If exact inference is impossible, several algorithms can be used to obtain approximate solutions. These include:
is usually done by maximum likelihood learning for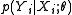 
.
If all nodes have exponential family distributions and all nodes are observed during training, this optimization
is convex. It can be solved for example using gradient descent
algorithms Quasi-Newton method
s, such as the L-BFGS
algorithm.
On the other hand, if some variables are unobserved, the inference problem has to be solved for these variables. This is intractable to do exact in general graphs, so approximations have to be used.
represents a sequence of observations and 
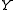represents a hidden (or unknown) state variable that needs to be inferred given the observations.
The
are structured to form a chain, with an edge between each 
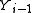and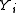 
. As well as having a simple interpretation of the 
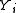as "labels" for each element in the input sequence, this layout admits efficient algorithms for:
The conditional dependency of each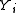
on 
is defined through a fixed set of feature functions of the form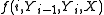 
, which can informally be thought of as measurements on the input sequence that partially determine the likelihood
of each possible value for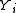
. The model assigns each feature a numerical weight and combines them to determine the probability of a certain value for 
.
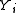Linear-chain CRFs have many of the same applications as conceptually simpler hidden Markov models (HMMs), but relax certain assumptions about the input and output sequence distributions. An HMM can loosely be understood as a CRF with very specific feature functions that use constant probabilities to model state transitions and emissions. Conversely, a CRF can loosely be understood as a generalization of an HMM that makes the constant transition probabilities into arbitrary functions that vary across the positions in the sequence of hidden states, depending on the input sequence.
Notably in contrast to HMMs, CRFs can contain any number of feature functions, the feature functions can inspect the entire input sequence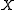
at any point during inference, and the range of the feature functions need not have a probabilistic interpretation.
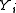dependent on a fixed number 
of previous variables 
. Training and inference are only practical for small values of 
(such as o ≤ 5), since their computational cost increases exponentially with 
. Large-margin models for structured prediction
, such as the structured Support Vector Machine
can be seen as an alternative training procedure to CRFs.
There exists another generalization of CRFs, the semi-Markov conditional random field (semi-CRF), which models variable-length segmentations of the label sequence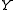
. This provides much of the power of higher-order CRFs to model long-range dependencies of the 
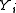, at a reasonable computational cost.
This is a partial list of software that implement CRF related tools.
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
often applied in pattern recognition
Pattern recognition
In machine learning, pattern recognition is the assignment of some sort of output value to a given input value , according to some specific algorithm. An example of pattern recognition is classification, which attempts to assign each input value to one of a given set of classes...
.
More specifically it is a type of discriminative
Discriminative model
Discriminative models are a class of models used in machine learning for modeling the dependence of an unobserved variable y on an observed variable x...
undirected probabilistic
Statistical model
A statistical model is a formalization of relationships between variables in the form of mathematical equations. A statistical model describes how one or more random variables are related to one or more random variables. The model is statistical as the variables are not deterministically but...
graphical model
Graphical model
A graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
. It is used to encode known relationships between observations and construct consistent interpretations. It is often used for labeling
Sequence labeling
In machine learning, sequence labeling is a type of pattern recognition task that involves the algorithmic assignment of a categorical label to each member of a sequence of observed values. A common example of a sequence labeling task is part of speech tagging, which seeks to assign a part of...
or parsing
Parsing
In computer science and linguistics, parsing, or, more formally, syntactic analysis, is the process of analyzing a text, made of a sequence of tokens , to determine its grammatical structure with respect to a given formal grammar...
of sequential data, such as natural language text
Natural language processing
Natural language processing is a field of computer science and linguistics concerned with the interactions between computers and human languages; it began as a branch of artificial intelligence....
or biological sequences
Bioinformatics
Bioinformatics is the application of computer science and information technology to the field of biology and medicine. Bioinformatics deals with algorithms, databases and information systems, web technologies, artificial intelligence and soft computing, information and computation theory, software...
and in computer vision
Computer vision
Computer vision is a field that includes methods for acquiring, processing, analysing, and understanding images and, in general, high-dimensional data from the real world in order to produce numerical or symbolic information, e.g., in the forms of decisions...
. Specifically, CRFs find applications in shallow parsing
Shallow parsing
Shallow parsing is an analysis of a sentence which identifies the constituents , but does not specify their internal structure, nor their role in the main sentence....
, named entity recognition
Named entity recognition
Named-entity recognition is a subtask of information extraction that seeks to locate and classify atomic elements in text into predefined categories such as the names of persons, organizations, locations, expressions of times, quantities, monetary values, percentages, etc.Most research on NER...
and gene finding
Gene prediction
In computational biology gene prediction or gene finding refers to the process of identifying the regions of genomic DNA that encode genes. This includes protein-coding genes as well as RNA genes, but may also include prediction of other functional elements such as regulatory regions...
, among other tasks, being an alternative to the related hidden Markov model
Hidden Markov model
A hidden Markov model is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved states. An HMM can be considered as the simplest dynamic Bayesian network. The mathematics behind the HMM was developed by L. E...
s. In computer vision, CRFs are often used for object recognition and image segmentation.
Description
Lafferty, McCallum and Pereira (2001) define a CRF on observations and random variables 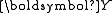as follows:Letbe a graph such that
, so that
is indexed by the vertices of
. Then
is a conditional random field in case,
when conditioned on, the random variables
obey the Markov property
Markov propertyIn probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
with
respect to the graph:, where
means
thatand
are neighbors in
.
What this means is that a CRF is an undirected graphical model
Graphical model
A graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
whose nodes can be divided into exactly two disjoint sets
and , the observed and output variables, respectively; the conditional distribution 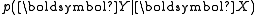is then modeled.Inference
For general graphs, the problem of exact inference in CRFs is intractable. The inference problem for a CRF is basically the same as for an MRF and the same arguments hold.However there exist special cases for which exact inference is feasible:
- If the graph is a chain or a tree, message passing algorithms yield exact solutions. The algorithms used in these cases are analogous to the forward-backward and Viterbi algorithmViterbi algorithmThe Viterbi algorithm is a dynamic programming algorithm for finding the most likely sequence of hidden states – called the Viterbi path – that results in a sequence of observed events, especially in the context of Markov information sources, and more generally, hidden Markov models...
for the case of HMMs. - If the CRF only contains pair-wise potentials and the energy is submodular, combinatorial min cut/max flow algorithms yield exact solutions.
If exact inference is impossible, several algorithms can be used to obtain approximate solutions. These include:
- Loopy belief propagation
- Alpha expansion
- Mean field inference
- Linear programming relaxations
Parameter Learning
Learning the parameters is usually done by maximum likelihood learning for 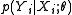.If all nodes have exponential family distributions and all nodes are observed during training, this optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
is convex. It can be solved for example using gradient descent
Gradient descent
Gradient descent is a first-order optimization algorithm. To find a local minimum of a function using gradient descent, one takes steps proportional to the negative of the gradient of the function at the current point...
algorithms Quasi-Newton method
Quasi-Newton method
In optimization, quasi-Newton methods are algorithms for finding local maxima and minima of functions. Quasi-Newton methods are based on...
s, such as the L-BFGS
L-BFGS
The limited-memory BFGS algorithm is a member of the broad family of quasi-Newton optimization methods that uses a limited memory variation of the Broyden–Fletcher–Goldfarb–Shanno update to approximate the inverse Hessian matrix...
algorithm.
On the other hand, if some variables are unobserved, the inference problem has to be solved for these variables. This is intractable to do exact in general graphs, so approximations have to be used.
Examples
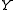In sequence modeling, the graph of interest is usually a chain graph. An input sequence of observed variables represents a sequence of observations and represents a hidden (or unknown) state variable that needs to be inferred given the observations.The
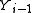are structured to form a chain, with an edge between each and 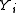. As well as having a simple interpretation of the 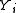as "labels" for each element in the input sequence, this layout admits efficient algorithms for:
- model training, learning the conditional distributions between the
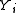and feature functions from some corpus of training data. - inference, determining the probability of a given label sequence
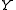given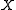 
. - decoding, determining the most likely label sequence
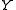given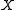 
.
The conditional dependency of each
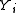on is defined through a fixed set of feature functions of the form 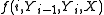, which can informally be thought of as measurements on the input sequence that partially determine the likelihoodLikelihood function
In statistics, a likelihood function is a function of the parameters of a statistical model, defined as follows: the likelihood of a set of parameter values given some observed outcomes is equal to the probability of those observed outcomes given those parameter values...
of each possible value for
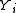. The model assigns each feature a numerical weight and combines them to determine the probability of a certain value for 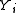.Linear-chain CRFs have many of the same applications as conceptually simpler hidden Markov models (HMMs), but relax certain assumptions about the input and output sequence distributions. An HMM can loosely be understood as a CRF with very specific feature functions that use constant probabilities to model state transitions and emissions. Conversely, a CRF can loosely be understood as a generalization of an HMM that makes the constant transition probabilities into arbitrary functions that vary across the positions in the sequence of hidden states, depending on the input sequence.
Notably in contrast to HMMs, CRFs can contain any number of feature functions, the feature functions can inspect the entire input sequence
at any point during inference, and the range of the feature functions need not have a probabilistic interpretation.Higher-order CRFs and semi-Markov CRFs
CRFs can be extended into higher order models by making each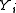 dependent on a fixed number of previous variables . Training and inference are only practical for small values of (such as o ≤ 5), since their computational cost increases exponentially with . Large-margin models for structured predictionStructured prediction
Structured prediction is an umbrella term for machine learning and regression techniques that involve predicting structured objects. For example, the problem of translating a natural language sentence into a semantic representation such as a parse tree can be seen as a structured prediction...
, such as the structured Support Vector Machine
Structured SVM
The structured support vector machine is a machine learning algorithm that generalizes the Support Vector Machine classifier. Whereas the SVM classifier supports binary classification, multiclass classification and regression, the structured SVM allows training of a classifier for general...
can be seen as an alternative training procedure to CRFs.
There exists another generalization of CRFs, the semi-Markov conditional random field (semi-CRF), which models variable-length segmentations of the label sequence
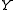. This provides much of the power of higher-order CRFs to model long-range dependencies of the 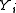, at a reasonable computational cost.Software
This is a partial list of software that implement generic CRF tools.- GCO CRFs with submodular energy functions (C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
) - GRMM General CRFs (JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - CRFall General CRFs (MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
) - Sarawagi's CRF Linear-chain CRFs (JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - HCRF library Hidden-state CRFs (C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
, MatlabMATLABMATLAB is a numerical computing environment and fourth-generation programming language. Developed by MathWorks, MATLAB allows matrix manipulations, plotting of functions and data, implementation of algorithms, creation of user interfaces, and interfacing with programs written in other languages,...
) - Wapiti Fast linear-chain CRFs (CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
) - CRFSuite Fast restricted linear-chain CRFs (CC (programming language)C is a general-purpose computer programming language developed between 1969 and 1973 by Dennis Ritchie at the Bell Telephone Laboratories for use with the Unix operating system....
) - CRF++ Linear-chain CRFs (C++C++C++ is a statically typed, free-form, multi-paradigm, compiled, general-purpose programming language. It is regarded as an intermediate-level language, as it comprises a combination of both high-level and low-level language features. It was developed by Bjarne Stroustrup starting in 1979 at Bell...
) - Monte Python Linear-chain CRFs (PythonPython (programming language)Python is a general-purpose, high-level programming language whose design philosophy emphasizes code readability. Python claims to "[combine] remarkable power with very clear syntax", and its standard library is large and comprehensive...
)
This is a partial list of software that implement CRF related tools.
- Conrad CRF based gene predictor (JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - Stanford NER Named Entity Recognizer (JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
) - BANNER Named Entity Recognizer (JavaJava (programming language)Java is a programming language originally developed by James Gosling at Sun Microsystems and released in 1995 as a core component of Sun Microsystems' Java platform. The language derives much of its syntax from C and C++ but has a simpler object model and fewer low-level facilities...
)
See also
- Graphical modelGraphical modelA graphical model is a probabilistic model for which a graph denotes the conditional independence structure between random variables. They are commonly used in probability theory, statistics—particularly Bayesian statistics—and machine learning....
- Markov random field
- Maximum entropy Markov modelMaximum entropy Markov modelIn machine learning, a maximum-entropy Markov model , or conditional Markov model , is a graphical model for sequence labeling that combines features of hidden Markov models and maximum entropy models...
(MEMM)
Further reading
- McCallum, A.: Efficiently inducing features of conditional random fields. In: Proc. 19th Conference on Uncertainty in Artificial Intelligence. (2003)
- Wallach, H.M.: Conditional random fields: An introduction. Technical report MS-CIS-04-21, University of Pennsylvania (2004)
- Sutton, C., McCallum, A.: An Introduction to Conditional Random Fields for Relational Learning. In "Introduction to Statistical Relational Learning". Edited by Lise Getoor and Ben Taskar. MIT Press. (2006) Online PDF
- Klinger, R., Tomanek, K.: Classical Probabilistic Models and Conditional Random Fields. Algorithm Engineering Report TR07-2-013, Department of Computer Science, Dortmund University of Technology, December 2007. ISSN 1864-4503. Online PDF