
Conformal Killing equation
Encyclopedia
In conformal geometry
, the conformal Killing equation on a manifold
of space-dimension
n with metric
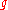 describes those vector fields
describes those vector fields  which preserve
which preserve 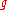 up to scale, i.e.
up to scale, i.e.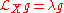
for some function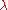 (where
(where  is the Lie derivative
is the Lie derivative
). Vector fields that satisfy the conformal Killing equation are exactly those vector fields whose flow
preserves the conformal structure of the manifold. The name Killing refers to Wilhelm Killing
, who first investigated the Killing equation for vector fields that preserve a Riemannian metric.
By taking the trace we find that necessarily . Therefore we can write the conformal Killing equation as
. Therefore we can write the conformal Killing equation as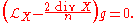
In abstract indices
where the round brackets denote symmetrization.
Conformal geometry
In mathematics, conformal geometry is the study of the set of angle-preserving transformations on a space. In two real dimensions, conformal geometry is precisely the geometry of Riemann surfaces...
, the conformal Killing equation on a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
of space-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
n with metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
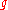 describes those vector fields
describes those vector fields  which preserve
which preserve 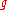 up to scale, i.e.
up to scale, i.e.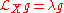
for some function
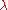 (where
(where  is the Lie derivative
is the Lie derivativeLie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
). Vector fields that satisfy the conformal Killing equation are exactly those vector fields whose flow
Flow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
preserves the conformal structure of the manifold. The name Killing refers to Wilhelm Killing
Wilhelm Killing
Wilhelm Karl Joseph Killing was a German mathematician who made important contributions to the theories of Lie algebras, Lie groups, and non-Euclidean geometry....
, who first investigated the Killing equation for vector fields that preserve a Riemannian metric.
By taking the trace we find that necessarily
 . Therefore we can write the conformal Killing equation as
. Therefore we can write the conformal Killing equation as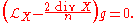
In abstract indices

where the round brackets denote symmetrization.

