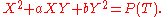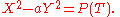Conic bundle
Encyclopedia
In algebraic geometry
, a conic bundle is an algebraic variety
that appears as a solution of a Cartesian equation of the form
Theoretically, it can be considered as a Severi–Brauer surface, or more precisely as a Châtelet surface
. This can be a double covering of a ruled surface
. Through an isomorphism, it can be associated with a symbol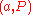
in the second Galois cohomology
of the field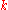
.
In fact, it is a surface with a well-understood divisor group and simplest cases share with Del Pezzo surface
s the property of being a rational surface
. But many problems of contemporary mathematics remain open, notably (for those examples which are not rational) the question of unirationality.
of the left hand side. Thus, after a harmless change, it has a simple expression like
In a second step, it should be placed in a projective space
in order to complete the surface "at infinity".
To do this, we write the equation in homogeneous coordinates
and expresses the first visible part of the fiber
That is not enough to complete the fiber as non-singular (clean and smooth), and then glue it to infinity by a change of classical maps:
Seen from infinity, (i.e. through the change
), the same fiber (excepted the fibers 
and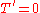 
), written as the set of solutions 
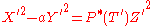where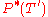 
appears naturally as the reciprocal polynomial of 
. Details are below about the map-change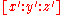 
.
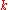is of characteristic zero and denote by 
any integer except zero. Denote by P(T) a polynomial with coefficients in the field 
, of degree 2m or 2m − 1, without multiple root. Consider the scalar a.
One defines the reciprocal polynomial by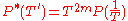
, and the conic bundle Fa,P as follows :
Definition:
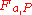is the surface obtained as "gluing" of the two surfaces 
and 
of equations
and
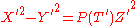
along the open sets by isomorphisms
and 
.
One shows the following result :
Fundamental property:
The surface Fa,P is a k clean and smooth surface, the mapping defined by
by
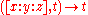
and the same on
gives to Fa,P a structure of conic bundle over P1,k.
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, a conic bundle is an algebraic variety
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
that appears as a solution of a Cartesian equation of the form
Theoretically, it can be considered as a Severi–Brauer surface, or more precisely as a Châtelet surface
Châtelet surface
In algebraic geometry, a Châtelet surface is a rational surface studied by given by an equationy^2-az^2=P \, where P has degree 3 or 4. They are conic bundles....
. This can be a double covering of a ruled surface
Ruled surface
In geometry, a surface S is ruled if through every point of S there is a straight line that lies on S. The most familiar examples are the plane and the curved surface of a cylinder or cone...
. Through an isomorphism, it can be associated with a symbol
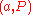in the second Galois cohomologyGalois cohomology
In mathematics, Galois cohomology is the study of the group cohomology of Galois modules, that is, the application of homological algebra to modules for Galois groups...
of the field
.In fact, it is a surface with a well-understood divisor group and simplest cases share with Del Pezzo surface
Del Pezzo surface
In mathematics, a del Pezzo surface or Fano surface is a two-dimensional Fano variety, in other words a non-singular projective algebraic surface with ample anticanonical divisor class...
s the property of being a rational surface
Rational surface
In algebraic geometry, a branch of mathematics, a rational surface is a surface birationally equivalent to the projective plane, or in other words a rational variety of dimension two...
. But many problems of contemporary mathematics remain open, notably (for those examples which are not rational) the question of unirationality.
A naive point of view
To write correctly a conic bundle, one must first reduce the quadratic formQuadratic form
In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....
of the left hand side. Thus, after a harmless change, it has a simple expression like
In a second step, it should be placed in a projective space
Projective space
In mathematics a projective space is a set of elements similar to the set P of lines through the origin of a vector space V. The cases when V=R2 or V=R3 are the projective line and the projective plane, respectively....
in order to complete the surface "at infinity".
To do this, we write the equation in homogeneous coordinates
Homogeneous coordinates
In mathematics, homogeneous coordinates, introduced by August Ferdinand Möbius in his 1827 work Der barycentrische Calcül, are a system of coordinates used in projective geometry much as Cartesian coordinates are used in Euclidean geometry. They have the advantage that the coordinates of points,...
and expresses the first visible part of the fiber
That is not enough to complete the fiber as non-singular (clean and smooth), and then glue it to infinity by a change of classical maps:
Seen from infinity, (i.e. through the change
), the same fiber (excepted the fibers and 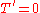), written as the set of solutions 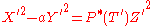where 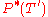appears naturally as the reciprocal polynomial of . Details are below about the map-change 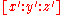.The fiber c
Going a little further, while simplifying the issue, limit to cases where the field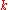 is of characteristic zero and denote by any integer except zero. Denote by P(T) a polynomial with coefficients in the field , of degree 2m or 2m − 1, without multiple root. Consider the scalar a.One defines the reciprocal polynomial by
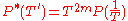, and the conic bundle Fa,P as follows :Definition:
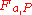is the surface obtained as "gluing" of the two surfaces and of equationsand
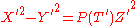
along the open sets by isomorphisms
and .One shows the following result :
Fundamental property:
The surface Fa,P is a k clean and smooth surface, the mapping defined by
by
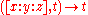
and the same on
gives to Fa,P a structure of conic bundle over P1,k.See also
- Algebraic surfaceAlgebraic surfaceIn mathematics, an algebraic surface is an algebraic variety of dimension two. In the case of geometry over the field of complex numbers, an algebraic surface has complex dimension two and so of dimension four as a smooth manifold.The theory of algebraic surfaces is much more complicated than that...
- Intersection number (algebraic geometry)
- List of complex and algebraic surfaces