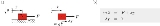
Contact dynamics
Encyclopedia
Contact dynamics deals with the motion of multibody system
s subjected to unilateral contact
s and friction
. Such systems are omnipresent in many multibody dynamics applications. Consider for example
In the following it is discussed how such mechanical systems with unilateral contacts and friction can be modeled and how the time evolution of such systems can be obtained by numerical integration
. In addition, some examples are given.
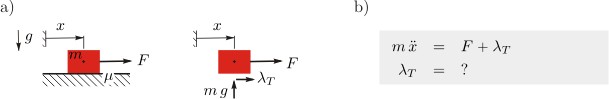
and require therefore special attention. In addition, oscillations may occur which are induced by the regularization. Also the choice of suitable regularization parameters is a problem. Considering a unilateral contact, the regularization parameter can be interpreted as contact stiffness. The regularization parameter of a friction element lacks such a physical interpretation. Considering a regularized friction law, also the sticking case is associated with small velocities, which does not correspond to the physical nature of friction. The regularized approach is related to the concept of regularization
.Normally one would use lube to reduce friction, because if there is too much kinetic friction it will turn in to static enabling you to move in
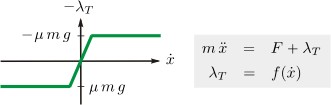
.
 To conclude, the non-smooth approach changes the underlying mathematical structure if required and leads to a proper description of mechanical systems with unilateral contacts and friction. As a consequence of the changing mathematical structure, impacts
To conclude, the non-smooth approach changes the underlying mathematical structure if required and leads to a proper description of mechanical systems with unilateral contacts and friction. As a consequence of the changing mathematical structure, impacts
can occur, and the time evolutions of the positions and the velocities can not be assumed to be smooth
anymore. As a consequence, additional impact equations and impact laws have to be defined. In order to handle the changing mathematical structure, the set-valued force laws are commonly written as inequality or inclusion problems. The evaluation of these inequalities/inclusions is commonly done by solving linear (or nonlinear) complementarity problems
, by quadratic programming
or by transforming the inequality/inclusion problems into projective equations which can be solved iteratively by Jacobi
or Gauss–Seidel techniques.
The non-smooth approach provides a new modeling approach for mechanical systems with unilateral contacts and friction, which incorporates also the whole classical mechanics subjected to bilateral constraints. The approach is associated to the classical DAE theory and leads to robust integration schemes.


Multibody system
A multibody system is used to model the dynamic behavior of interconnected rigid or flexible bodies, each of which may undergo large translational and rotational displacements.- Introduction :...
s subjected to unilateral contact
Unilateral contact
In mechanics, a unilateral contact denotes a mechanical constraint which prevents penetration between two bodies; see figure 1a. These bodies may be rigid or flexible...
s and friction
Friction
Friction is the force resisting the relative motion of solid surfaces, fluid layers, and/or material elements sliding against each other. There are several types of friction:...
. Such systems are omnipresent in many multibody dynamics applications. Consider for example
- Contacts between wheels and ground in vehicle dynamicsVehicle dynamicsVehicle dynamics refers to the dynamics of vehicles, here assumed to be ground vehicles. Vehicle dynamics is a part of engineering primarily based on classical mechanics but it may also involve chemistry, solid state physics, electrical engineering, communications, psychology, control theory,...
- Squealing of brakes due to friction induced oscillations
- Motion of many particles, spheres which fall in a funnel, mixing processes (granular media)
- ClockworkClockworkA clockwork is the inner workings of either a mechanical clock or a device that operates in a similar fashion. Specifically, the term refers to a mechanical device utilizing a complex series of gears....
s - Walking machines
- Arbitrary machines with limit stops, friction.
In the following it is discussed how such mechanical systems with unilateral contacts and friction can be modeled and how the time evolution of such systems can be obtained by numerical integration
Numerical ordinary differential equations
Numerical ordinary differential equations is the part of numerical analysis which studies the numerical solution of ordinary differential equations...
. In addition, some examples are given.
Modeling
The two main approaches for modeling mechanical systems with unilateral contacts and friction are the regularized and the non-smooth approach. In the following, the two approaches are introduced using a simple example. Consider a block which can slide or stick on a table, see figure 1a. The motion of the block is described by the equation of motion, whereas the friction force is unknown, see figure 1b. In order to obtain the friction force, a separate force law must be specified which links the friction force to the associated velocity of the block.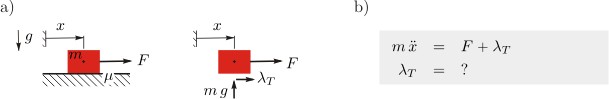
Regularized approach
A regularized force law for friction writes the friction force as function of the velocity, see figure 2. Doing so, one can eliminate the friction force to obtain a system of ordinary differential equations. A regularized force law for a unilateral contact corresponds to a spring whose stiffness vanishes for an open contact. The regularized approach is easy to understand but has numerical drawbacks in application. The resulting ordinary differential equations are stiffStiff equation
In mathematics, a stiff equation is a differential equation for which certain numerical methods for solving the equation are numerically unstable, unless the step size is taken to be extremely small. It has proved difficult to formulate a precise definition of stiffness, but the main idea is that...
and require therefore special attention. In addition, oscillations may occur which are induced by the regularization. Also the choice of suitable regularization parameters is a problem. Considering a unilateral contact, the regularization parameter can be interpreted as contact stiffness. The regularization parameter of a friction element lacks such a physical interpretation. Considering a regularized friction law, also the sticking case is associated with small velocities, which does not correspond to the physical nature of friction. The regularized approach is related to the concept of regularization
Regularization (physics)
-Introduction:In physics, especially quantum field theory, regularization is a method of dealing with infinite, divergent, and non-sensical expressions by introducing an auxiliary concept of a regulator...
.Normally one would use lube to reduce friction, because if there is too much kinetic friction it will turn in to static enabling you to move in
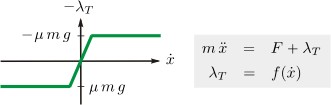
Non-smooth approach
A more sophisticated approach is the non-smooth approach, which uses set-valued force laws to model mechanical systems with unilateral contacts and friction. Consider again the block which slides or sticks on the table. The associated set-valued friction law of type Sgn is depicted in figure 3. Regarding the sliding case, the friction force is given. Regarding the sticking case, the friction force is set-valued and determined according to an additional algebraic constraintConstraint (mathematics)
In mathematics, a constraint is a condition that a solution to an optimization problem must satisfy. There are two types of constraints: equality constraints and inequality constraints...
.

Impact force
In mechanics, an impact is a high force or shock applied over a short time period when two or more bodies collide. Such a force or acceleration usually has a greater effect than a lower force applied over a proportionally longer time period of time...
can occur, and the time evolutions of the positions and the velocities can not be assumed to be smooth
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
anymore. As a consequence, additional impact equations and impact laws have to be defined. In order to handle the changing mathematical structure, the set-valued force laws are commonly written as inequality or inclusion problems. The evaluation of these inequalities/inclusions is commonly done by solving linear (or nonlinear) complementarity problems
Linear complementarity problem
In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...
, by quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
or by transforming the inequality/inclusion problems into projective equations which can be solved iteratively by Jacobi
Jacobi method
In numerical linear algebra, the Jacobi method is an algorithm for determining the solutions of a system of linear equations with largest absolute values in each row and column dominated by the diagonal element. Each diagonal element is solved for, and an approximate value plugged in. The process...
or Gauss–Seidel techniques.
The non-smooth approach provides a new modeling approach for mechanical systems with unilateral contacts and friction, which incorporates also the whole classical mechanics subjected to bilateral constraints. The approach is associated to the classical DAE theory and leads to robust integration schemes.
Numerical Integration
The integration of regularized models can be done by standard stiff solvers for ordinary differential equations. However, oscillations induced by the regularization can occur. Considering non-smooth models of mechanical systems with unilateral contacts and friction, two main classes of integrators exist, the event-driven and the so-called time-stepping integrators.Event-driven integrators
Event-driven integrators distinguish between smooth parts of the motion in which the underlying structure of the differential equations does not change, and in events or so-called switching points at which this structure changes, i.e. time instants at which a unilateral contact closes or a stick slip transition occurs. A these switching points, the set-valued force (and additional impact) laws are evaluated in order to obtain a new underlying mathematical structure on which the integration can be continued. Event-driven integrators are very accurate but are not suitable for systems with many contacts.Time-stepping integrators
So-called time-stepping integrators are dedicated numerical schemes for mechanical systems with many contacts. The first time-stepping integrator was introduced by J.J. Moreau. The integrators do not aim at resolving switching points and are therefore very robust in application. As the integrators do work with the integral of the contact forces and not with the forces itself, the methods can handle both non-impulsive motion and impulsive events like impacts. As a drawback, the accuracy of time-stepping integrators is low. This lack can be fixed by using a step-size refinement at switching points. Smooth parts of the motion are processed by larger step sizes, and higher order integration methods can be used to increase the integration order.Examples
This section gives some examples of mechanical systems with unilateral contacts and friction. The results have been obtained by a non-smooth approach using time-stepping integrators.Granular matters
Time-stepping methods are especially well suited for the simulation of granular materials. Figure 4 depicts the simulation of 1000 disks which are mixed.
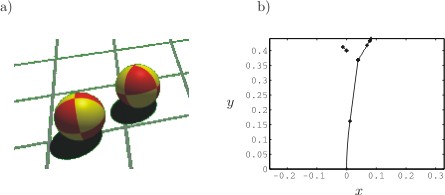
Billiard
Consider two colliding spheres in a billiard play. Figure 5a shows some snapshots of two colliding spheres, figure 5b depicts the associated trajectories.
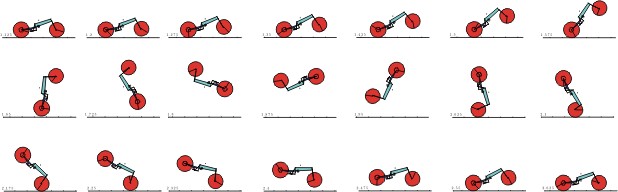
Wheely of a motorbike
If a motorbike is accelerated too fast, it makes a wheely. Figure 6 shows some snapshots of a simulation.
Motion of the woodpecker toy
The woodpecker toy is a well known benchmark problem in contact dynamics. The toy consists of a pole, a sleeve with a hole that is slightly larger than the diameter of the pole, a spring and the woodpecker body. In operation, the woodpecker moves down the pole performing some kind of pitching motion, which is controlled by the sleeve. Figure 7 shows some snapshots of a simulation.
See also
- Multibody dynamicsMultibody systemA multibody system is used to model the dynamic behavior of interconnected rigid or flexible bodies, each of which may undergo large translational and rotational displacements.- Introduction :...
- Contact mechanicsContact mechanicsContact mechanics is the study of the deformation of solids that touch each other at one or more points. The physical and mathematical formulation of the subject is built upon the mechanics of materials and continuum mechanics and focuses on computations involving elastic, viscoelastic, and plastic...
: Applications with unilateral contacts and friction. Static applications (contact between deformable bodies) and dynamic applications (Contact dynamics). - Lubachevsky-Stillinger algorithmLubachevsky-Stillinger algorithmLubachevsky-Stillinger algorithm isa numerical procedure that simulates or imitatesa physical process of compressing an assemblyof hard particles...
of simulating compression of large assemblies of hard particles
Further reading
- Acary V. and Brogliato, B. Numerical Methods for Nonsmooth Dynamical Systems. Applications in Mechanics and Electronics. Springer Verlag, LNACM 35, Heidelberg, 2008.
- Brogliato B. Nonsmooth Mechanics. Communications and Control Engineering Series Springer-Verlag, London, 1999 (2nd Ed.)
- Glocker, Ch. Dynamik von Starrkoerpersystemen mit Reibung und Stoessen, volume 18/182 of VDI Fortschrittsberichte Mechanik/Bruchmechanik. VDI Verlag, Düsseldorf, 1995
- Glocker Ch. and Studer C. Formulation and preparation for Numerical Evaluation of Linear Complementarity Systems. Multibody System Dynamics 13(4):447-463, 2005
- Jean M. The non-smooth contact dynamics method. Computer Methods in Applied mechanics and Engineering 177(3-4):235-257, 1999
- Moreau J.J. Unilateral Contact and Dry Friction in Finite Freedom Dynamics, volume 302 of Non-smooth Mechanics and Applications, CISM Courses and Lectures. Springer, Wien, 1988
- Pfeiffer F., Foerg M. and Ulbrich H. Numerical aspects of non-smooth multibody dynamics. Comput. Methods Appl. Mech. Engrg 195(50-51):6891-6908, 2006
- Potra F.A., Anitescu M., Gavrea B. and Trinkle J. A linearly implicit trapezoidal method for integrating stiff multibody dynamics with contacts, joints and friction. Int. J. Numer. Meth. Engng 66(7):1079-1124, 2006
- Stewart D.E. and Trinkle J.C. An Implicit Time-Stepping Scheme for Rigid Body Dynamics with Inelastic Collisions and Coulomb Friction. Int. J. Numer. Methods Engineering 39(15):2673-2691, 1996
- Studer C. Augmented time-stepping integration of non-smooth dynamical systems, PhD Thesis ETH Zurich, ETH E-Collection, to appear 2008
- Studer C. Numerics of Unilateral Contacts and Friction—Modeling and Numerical Time Integration in Non-Smooth Dynamics, Lecture Notes in Applied and Computational Mechanics, Volume 47, Springer, Berlin, Heidelberg, 2009
External links
- Multibody research group, Center of Mechanics, ETH Zurich.
- Lehrstuhl für angewandte Mechanik TU Munich.
- BiPoP Team, INRIA Rhone-Alpes, France,
- Multibody dynamics, Rensselaer Polytechnic Institute.
- Siconos software
- dynamY software
- LMGC90 software
- Solfec software

