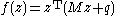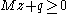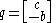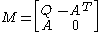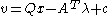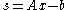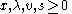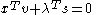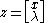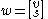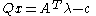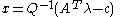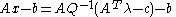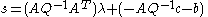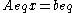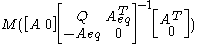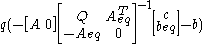Linear complementarity problem
Encyclopedia
In mathematical optimization theory
, the linear complementarity problem (LCP) arises frequently in computational mechanics
and encompasses the well-known quadratic programming
as a special case. It was proposed by Cottle and Dantzig
A sufficient condition for existence and uniqueness of a solution to this problem is that M be symmetric positive-definite
.
The vector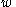
is a slack variable
, and so is generally discarded after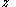
is found. As such, the problem can also be formulated as:
subject to the constraints
These constraints ensure that f is always non-negative. The minimum of f is 0 at z if and only if z solves the linear complementarity problem.
If M is positive definite
, any algorithm for solving (strictly) convex QPs
can solve the LCP. Specially designed basis-exchange pivoting algorithms, such as Lemke's algorithm
and a variant of the simplex algorithm of Dantzig
have been used for decades. Besides having polynomial time complexity, interior-point methods are also effective in practice.
Also, a quadratic-programming problem stated as minimize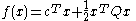
subject to 
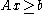as well as 
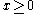with Q symmetric
is the same as solving the LCP with
This is because the Karush–Kuhn–Tucker conditions of the QP problem can be written as:
...being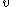
the Lagrange multipliers on the non-negativity constraints,
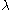the multipliers on the inequality constraints, and 
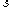the slack variables for the inequality constraints. The fourth condition derives from the complementarity of each group of variables (
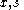) with its set of KKT vectors (optimal Lagrange multipliers) being (
).
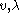In that case,
If the non-negativity constraint on the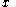
is relaxed, the dimensionality of the LCP problem can be reduced to the number of the inequalities, as long as 
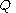is non-singular (which is guaranteed if it is positive definite
). The multipliers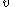
are no longer present, and the first KKT conditions can be rewritten as:
or:
pre-multiplying the two sides by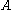
and subtracting 
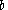we obtain:
The left side, due to the second KKT condition, is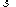
. Substituting and reordering:
Calling now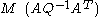
and 
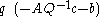we have an LCP, due to the relation of complementarity between the slack variables 
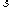and their Lagrange multipliers 
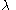. Once we solve it, we may obtain the value of 
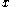from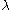 
through the first KKT condition.
Finally, it is also possible to handle additional equality constraints:
This introduces a vector of Lagrange multipliers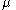
, with the same dimension as 
.
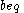It is easy to verify that the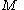
and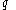 
for the LCP system 
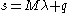are now expressed as:
From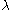
we can now recover the values of both 
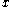and the Lagrange multiplier of equalities 
:
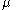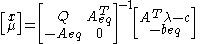
In fact, most QP solvers work on the LCP formulation, including the interior point method
, principal / complementarity pivoting, and active set methods. LCP problems can be solved also by the criss-cross algorithm
, conversely, for linear complementarity problems, the criss-cross algorithm terminates finitely only if the matrix is a sufficient matrix. A sufficient matrix is a generalization both of a positive-definite matrix
and of a P-matrix, whose principal minors are each positive.
Such LCPs can be solved when they are formulated abstractly using oriented-matroid
theory.
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, the linear complementarity problem (LCP) arises frequently in computational mechanics
Computational mechanics
Computational mechanics is the discipline concerned with the use of computational methods to study phenomena governed by the principles of mechanics. Before the emergence of computational science as a "third way" besides theoretical and experimental sciences, computational mechanics was widely...
and encompasses the well-known quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
as a special case. It was proposed by Cottle and Dantzig
George Dantzig
George Bernard Dantzig was an American mathematical scientist who made important contributions to operations research, computer science, economics, and statistics....
Formulation
Given a real matrix M and vector q, the linear complementarity problem seeks vectors z and w which satisfy the following constraints:-
-
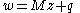
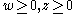(that is, each component of these two vectors is non-negative) -
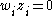for all i. (The complementarityComplementarity theoryA complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...
condition)
A sufficient condition for existence and uniqueness of a solution to this problem is that M be symmetric positive-definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
.
The vector
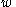is a slack variableSlack variable
In an optimization problem, a slack variable is a variable that is added to an inequality constraint to transform it to an equality. Introducing a slack variable replaces an inequality constraint with an equality constraint and a nonnegativity constraint....
, and so is generally discarded after
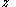is found. As such, the problem can also be formulated as:-
-
-
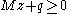
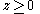
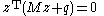(the complementarity condition)
Convex quadratic-minimization: Minimum conditions
Finding a solution to the linear complementarity problem is associated with minimizing the quadratic function
subject to the constraints
These constraints ensure that f is always non-negative. The minimum of f is 0 at z if and only if z solves the linear complementarity problem.
If M is positive definite
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
, any algorithm for solving (strictly) convex QPs
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
can solve the LCP. Specially designed basis-exchange pivoting algorithms, such as Lemke's algorithm
Lemke's algorithm
In mathematical optimization, Lemke's algorithm is an procedure for solving linear complementarity problems, and more generally mixed linear complementarity problems.Lemke's algorithm is of pivoting or basis-exchange type...
and a variant of the simplex algorithm of Dantzig
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
have been used for decades. Besides having polynomial time complexity, interior-point methods are also effective in practice.
Also, a quadratic-programming problem stated as minimize
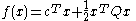subject to 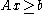as well as 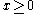with Q symmetricis the same as solving the LCP with
This is because the Karush–Kuhn–Tucker conditions of the QP problem can be written as:
...being
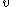the Lagrange multipliers on the non-negativity constraints, 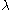the multipliers on the inequality constraints, and 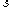the slack variables for the inequality constraints. The fourth condition derives from the complementarity of each group of variables (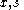) with its set of KKT vectors (optimal Lagrange multipliers) being (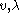).In that case,
If the non-negativity constraint on the
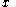is relaxed, the dimensionality of the LCP problem can be reduced to the number of the inequalities, as long as 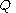is non-singular (which is guaranteed if it is positive definitePositive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
). The multipliers
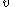are no longer present, and the first KKT conditions can be rewritten as:
or:
pre-multiplying the two sides by
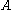and subtracting 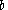we obtain:
The left side, due to the second KKT condition, is
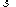. Substituting and reordering:
Calling now
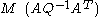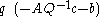and we have an LCP, due to the relation of complementarity between the slack variables 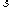and their Lagrange multipliers 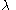. Once we solve it, we may obtain the value of 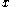from 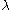through the first KKT condition.Finally, it is also possible to handle additional equality constraints:
This introduces a vector of Lagrange multipliers
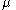, with the same dimension as 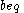.It is easy to verify that the
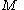and 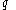for the LCP system 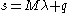are now expressed as:
From
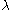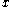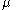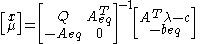
we can now recover the values of both and the Lagrange multiplier of equalities :In fact, most QP solvers work on the LCP formulation, including the interior point method
Interior point method
Interior point methods are a certain class of algorithms to solve linear and nonlinear convex optimization problems.The interior point method was invented by John von Neumann...
, principal / complementarity pivoting, and active set methods. LCP problems can be solved also by the criss-cross algorithm
Criss-cross algorithm
In mathematical optimization, the criss-cross algorithm denotes a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for...
, conversely, for linear complementarity problems, the criss-cross algorithm terminates finitely only if the matrix is a sufficient matrix. A sufficient matrix is a generalization both of a positive-definite matrix
Positive-definite matrix
In linear algebra, a positive-definite matrix is a matrix that in many ways is analogous to a positive real number. The notion is closely related to a positive-definite symmetric bilinear form ....
and of a P-matrix, whose principal minors are each positive.
Such LCPs can be solved when they are formulated abstractly using oriented-matroid
Oriented matroid
An oriented matroid is a mathematical structure that abstracts the properties of directed graphs and of arrangements of vectors in a vector space over an ordered field...
theory.
See also
- Complementarity theoryComplementarity theoryA complementarity problem is a type of mathematical optimization problem. It is the problem of optimizing a function of two vector variables subject to certain requirements which include: that the inner product of the two variables must equal zero, i.e. = 0...
- Physics enginePhysics engineA physics engine is computer software that provides an approximate simulation of certain physical systems, such as rigid body dynamics , soft body dynamics, and fluid dynamics, of use in the domains of computer graphics, video games and film. Their main uses are in video games , in which case the...
Impulse/constraint type physics engines for games use this approach.
Further reading
- R. W. Cottle and G. B. Dantzig. Complementary pivot theory of mathematical programming. Linear Algebra and its Applications, 1:103-125, 1968.
External links
- LCPSolve — A simple procedure in GAUSS to solve a linear complementarity problem
- LCPSolve.py — A Python/NumPy implementation of LCPSolve is part of OpenOptOpenOptOpenOpt is an open-source framework for numerical optimization, nonlinear equations and systems of them. It is licensed under the BSD license, making it available to be used in both open- and closed-code software. The package already has some essential ....
since its release 0.32