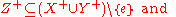Oriented matroid
Encyclopedia
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
structure
Mathematical structure
In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....
that abstracts the properties of directed graph
Directed graph
A directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
s and of arrangements of vectors in a vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over an ordered field
Ordered field
In mathematics, an ordered field is a field together with a total ordering of its elements that is compatible with the field operations. Historically, the axiomatization of an ordered field was abstracted gradually from the real numbers, by mathematicians including David Hilbert, Otto Hölder and...
(particularly for partially ordered vector space
Ordered vector space
In mathematics an ordered vector space or partially ordered vector space is a vector space equipped with a partial order which is compatible with the vector space operations.- Definition:...
s). In comparison, an ordinary (i.e., non-oriented) matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
abstracts the dependence
Linear independence
In linear algebra, a family of vectors is linearly independent if none of them can be written as a linear combination of finitely many other vectors in the collection. A family of vectors which is not linearly independent is called linearly dependent...
properties that are common both to graphs
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
, which are not necessarily directed, and to arrangements of vectors over field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
s, which are not necessarily ordered.
All oriented matroids have an underlying matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
. Thus, results on ordinary matroids can be applied to oriented matroids. However, the converse is false; some matroids cannot become an oriented matroid by orienting an underlying structure (e.g., circuits or independent sets).
The distinction between matroids and oriented matroids is discussed further below.
Matroids are often useful in areas such as dimension theory
Dimension theory (algebra)
In mathematics, dimension theory is a branch of commutative algebra studying the notion of the dimension of a commutative ring, and by extension that of a scheme.-References:* Part II of .* Chapter 10 of ....
and algorithms.
Because of an oriented matroid's inclusion of additional details about the oriented nature of a structure,
its usefulness extends further into several areas including geometry
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and optimization
Optimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
.
Axiomatizations
Like ordinary matroids, several equivalent systems of axiomsAxiomatic system
In mathematics, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A mathematical theory consists of an axiomatic system and all its derived theorems...
exist.
(Such structures that possess multiple equivalent axiomatizations are called cryptomorphic
Cryptomorphism
In mathematics, two objects, especially systems of axioms or semantics for them, are called cryptomorphic if they are equivalent but not obviously equivalent...
.)
Signed sets
Before we list the circuit axioms a few terms must be defined.- A signed set,
, combines a set of objects 
with a partition of that set into two subsets: 
and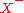 
.
- The members of
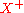are called the positive elements; members of 
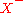are the negative elements.
- The set
is called the support of 
.
- The empty signed set,
is defined in the obvious way.
- The signed set
is the opposite of 
, i.e.,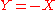 
, if and only if 
and 
The concept of signed sets is key to distinguishing oriented from ordinary matroids.
Axioms
Let
be any set. We refer to 
as the ground set.Let
be a collection of signed sets, each of which is supported by a subset of 
.If the following axioms hold for
, then equivalently 
is the set of signed circuitsfor an oriented matroid on
.- (C0)
- (C1) (symmetric)
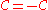
- (C2) (incomparable)
- (C3) (weak elimination)
-
Examples
Oriented matroids are often introduced (e.g., Bachem and Kern) as an abstraction for directed graphs or systems of linear inequalities.Thus, it may be helpful to first be knowledgeable of the structures for which oriented matroids are an abstraction. Several of these topics are listed below.
Linear optimization
Albert W. Tucker
Albert William Tucker was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming....
studies of such sign patterns in "Tucker tableaux".
Much of the theory of oriented matroids (OMs) was developed to study the combinatorial invariants of linear-optimization, particularly those visible in the basis-exchange pivoting of the simplex algorithm.
Convex polytope
For example, Ziegler introduces oriented matroids via convex polytopes.Algebra: duality and polarity
Oriented matroids have a satisfying theory of dualityDuality (mathematics)
In mathematics, a duality, generally speaking, translates concepts, theorems or mathematical structures into other concepts, theorems or structures, in a one-to-one fashion, often by means of an involution operation: if the dual of A is B, then the dual of B is A. As involutions sometimes have...
.
Geometry
The theory of oriented matroids has influenced the development of combinatorial geometry, especially the theory of convex polytopeConvex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
s, zonotopes, and of configurations of vectors (arrangements of hyperplanes
Arrangement of hyperplanes
In geometry and combinatorics, an arrangement of hyperplanes is a finite set A of hyperplanes in a linear, affine, or projective space S....
). Many results—Carathéodory's theorem
Carathéodory's theorem (convex hull)
In convex geometry Carathéodory's theorem states that if a point x of Rd lies in the convex hull of a set P, there is a subset P′ of P consisting of d+1 or fewer points such that x lies in the convex hull of P′. Equivalently, x lies in an r-simplex with vertices in P, where r \leq d...
, Helly's theorem
Helly's theorem
Helly's theorem is a basic result in discrete geometry describing the ways that convex sets may intersect each other. It was discovered by Eduard Helly in 1913, but not published by him until 1923, by which time alternative proofs by and had already appeared...
, Radon's theorem
Radon's theorem
In geometry, Radon's theorem on convex sets, named after Johann Radon, states that any set of d + 2 points in Rd can be partitioned into two sets whose convex hulls intersect...
, the Hahn–Banach theorem
Hahn–Banach theorem
In mathematics, the Hahn–Banach theorem is a central tool in functional analysis. It allows the extension of bounded linear functionals defined on a subspace of some vector space to the whole space, and it also shows that there are "enough" continuous linear functionals defined on every normed...
, the Krein–Milman theorem, the lemma of Farkas—can be formulated using appropriate oriented matroids.
Rank 3 oriented matroids are equivalent to arrangements
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
of pseudolines.
Similarly, matroid theory is useful for developing combinatorial notions of dimension
Dimension (vector space)
In mathematics, the dimension of a vector space V is the cardinality of a basis of V. It is sometimes called Hamel dimension or algebraic dimension to distinguish it from other types of dimension...
, rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
, etc.
In combinatorial convexity, the notion of an antimatroid
Antimatroid
In mathematics, an antimatroid is a formal system that describes processes in which a set is built up by including elements one at a time, and in which an element, once available for inclusion, remains available until it is included...
is also useful.
Optimization
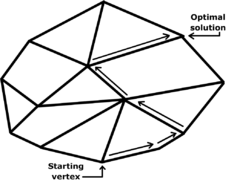
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
. In linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
, OM theory was the language in which Bland formulated his pivoting rule
Bland's rule
In mathematical optimization, Bland's rule is an algorithmic refinement of the simplex method for linear optimization....
by which the simplex algorithm
Simplex algorithm
In mathematical optimization, Dantzig's simplex algorithm is a popular algorithm for linear programming. The journal Computing in Science and Engineering listed it as one of the top 10 algorithms of the twentieth century....
avoids cycles; similarly, OM theory was used by Terlakey and Zhang to prove that their criss-cross algorithm
Criss-cross algorithm
In mathematical optimization, the criss-cross algorithm denotes a family of algorithms for linear programming. Variants of the criss-cross algorithm also solve more general problems with linear inequality constraints and nonlinear objective functions; there are criss-cross algorithms for...
s have finite termination for linear programming
Linear programming
Linear programming is a mathematical method for determining a way to achieve the best outcome in a given mathematical model for some list of requirements represented as linear relationships...
problems. Similar results were made in convex quadratic programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
by Todd and Terlaky. The criss-cross algorithm is often studied using the theory of oriented matroids (OMs), which is a combinatorial
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
abstraction of linear-optimization theory.
Historically, an OM algorithm for quadratic-programming problems
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
and linear-complementarity problem
Linear complementarity problem
In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...
s was published by Michael J. Todd, before Terlaky and Wang published their criss-cross algorithms. However, Todd's pivoting-rule cycles on nonrealizable oriented matroids (and only on nonrealizable oriented matroids). Such cycling does not stump the OM criss-cross algorithms of Terlaky and Wang, however. There are oriented-matroid variants of the criss-cross algorithm for linear programming, for quadratic programming, and for the linear-complementarity problem. Oriented matroid theory is used in many areas of optimization, besides linear programming. OM theory has been applied to linear-fractional programming
Linear-fractional programming
In mathematical optimization, linear-fractional programming is a generalization of linear programming . Whereas the objective function in linear programs are linear functions, the objective function in a linear-fractional program is a ratio of two linear functions...
quadratic-programming
Quadratic programming
Quadratic programming is a special type of mathematical optimization problem. It is the problem of optimizing a quadratic function of several variables subject to linear constraints on these variables....
problems, and linear complementarity problem
Linear complementarity problem
In mathematical optimization theory, the linear complementarity problem arises frequently in computational mechanics and encompasses the well-known quadratic programming as a special case...
s.
Outside of combinatorial optimization
Combinatorial optimization
In applied mathematics and theoretical computer science, combinatorial optimization is a topic that consists of finding an optimal object from a finite set of objects. In many such problems, exhaustive search is not feasible...
, OM theory also appears in convex minimization in Rockafellar's theory of "monotropic programming" and related notions of "fortified descent".
Similarly, matroid theory
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
has influenced the development of combinatorial algorithms, particularly the greedy algorithm
Greedy algorithm
A greedy algorithm is any algorithm that follows the problem solving heuristic of making the locally optimal choice at each stagewith the hope of finding the global optimum....
. More generally, a greedoid
Greedoid
In combinatorics, a greedoid is a type of set system. It arises from the notion of the matroid, which was originally introduced by Whitney in 1935 to study planar graphs and was later used by Edmonds to characterize a class of optimization problems that can be solved by greedy algorithms...
is useful for studying the finite termination of algorithms.
Books
- A. Bachem and W. Kern. Linear Programming Duality: An Introduction to Oriented Matroids. Universitext. Springer-Verlag, 1992.
- Evar D. Nering and Albert W. TuckerAlbert W. TuckerAlbert William Tucker was a Canadian-born American mathematician who made important contributions in topology, game theory, and non-linear programming....
, 1993, Linear Programs and Related Problems, Academic Press. (elementary) - R. T. Rockafellar. Network Flows and Monotropic Optimization, Wiley-Interscience, 1984 (610 pages); republished by Athena Scientific of Dimitri BertsekasDimitri BertsekasDimitri Bertsekas is an applied mathematician and computer scientist, and a professor at the department of Electrical Engineering and Computer Science at the Massachusetts Institute of Technology , Cambridge, Massachusetts.- Biography :...
, 1998. - Ziegler, Günter M.Günter M. ZieglerGünter M. Ziegler is a German mathematician. Ziegler is known for his research in discrete mathematics and geometry, and particularly on the combinatorics of polytopes.- Biography :...
, Lectures on Polytopes, Springer-Verlag, New York, 1994. - Richter-Gebert, J. and G. ZieglerGünter M. ZieglerGünter M. Ziegler is a German mathematician. Ziegler is known for his research in discrete mathematics and geometry, and particularly on the combinatorics of polytopes.- Biography :...
, Oriented Matroids, In Handbook of Discrete and Computational Geometry, J. Goodman and J.O'Rourke, (eds.), CRC Press, Boca Raton, 1997, p. 111-132.
Articles
- A. Bachem, A. Wanka, Separation theorems for oriented matroids, Discrete Math. 70 (1988) 303—310.
- R.G. Bland, New finite pivoting rules for the simplex method, Math. Oper. Res. 2 (1977) 103–107.
- Jon FolkmanJon FolkmanJon Hal Folkman was an American mathematician, a student of John Milnor, and a researcher at the RAND Corporation.-Schooling:Folkman was a Putnam Fellow in 1960. He received his Ph.D...
and James Lawrence, Oriented Matroids, J. Combin. Theory Ser. B 25 (1978) 199—236. - R. T. Rockafellar. The elementary vectors of a subspace of
, in Combinatorial Mathematics and its Applications, R. C. Bose and T. A. Dowling (eds.), Univ. of North Carolina Press, 1969, 104-127. - Michael J. Todd, Linear and quadratic programming in oriented matroids, J. Combin. Theory Ser. B 39 (1985) 105—133.
External links
- Komei Fukuda (ETH Zentrum, Zurich) with publications including [ftp://ftp.ifor.math.ethz.ch/pub/fukuda/reports/fukuda1982thesis.pdf Oriented matroid programming (1982 Ph.D. thesis)]
- Tamás Terlaky (Lehigh University) with publications