Arrangement of hyperplanes
Encyclopedia
In geometry
and combinatorics
, an arrangement of hyperplanes is a finite set A of hyperplane
s in a linear, affine
, or projective
space S.
Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice.
The intersection semilattice
of A, written L(A), is the set of all subspaces
that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These subspaces are called the flats of A. L(A) is partially ordered by reverse inclusion.
If the whole space S is 2-dimensional, the hyperplanes are line
s; such an arrangement is often called an arrangement of lines
. Historically, real arrangements of lines were the first arrangements investigated. If S is 3-dimensional one has an arrangement of planes.
If the arrangement is linear or projective, or if the intersection of all hyperplanes is nonempty, the intersection lattice is a geometric lattice.
(This is why the semilattice must be ordered by reverse inclusion—rather than by inclusion, which might seem more natural but would not yield a geometric (semi)lattice.)
When L(A) is a lattice, the matroid
of A, written M(A), has A for its ground set and has rank function r(S) := codim(I), where S is any subset of A and I is the intersection of the hyperplanes in S. In general, when L(A) is a semilattice, there is an analogous matroid-like structure that might be called a semimatroid, which is a generalization of a matroid (and has the same relationship to the intersection semilattice as does the matroid to the lattice in the lattice case), but is not a matroid if L(A) is not a lattice.
The characteristic polynomial of A, written pA(y), can be defined by
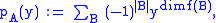
summed over all subsets B of A except, in the affine case, subsets whose intersection is empty. (The dimension of the empty set is defined to be −1.) This polynomial helps to solve some basic questions; see below.
Another polynomial associated with A is the Whitney-number polynomial wA(x, y), defined by
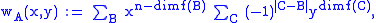
summed over B ⊆ C ⊆ A such that f(B) is nonempty.
Being a geometric lattice or semilattice, L(A) has a characteristic polynomial, pL(A)(y), which has an extensive theory (see matroid). Thus it is good to know that pA(y) = yi pL(A)(y), where i is the smallest dimension of any flat, except that in the projective case it equals yi + 1pL(A)(y).
The Whitney-number polynomial of A is similarly related to that of L(A).
(The empty set is excluded from the semilattice in the affine case specifically so that these relationships will be valid.)
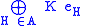
generated by the hyperplanes.
A chain complex
structure is defined on E with the usual boundary operator
.
The Orlik-Solomon algebra is then the quotient of E by the ideal
generated by elements of the form
(where 
have an empty intersection) and by boundaries of elements of the same form for which 
has codimension
less than p.
affine space
, the complement is disconnected: it is made up of separate pieces called cells or regions or chambers, each of which is either a bounded region that is a convex
polytope
, or an unbounded region that is a convex polyhedral region which goes off to infinity.
Each flat of A is also divided into pieces by the hyperplanes that do not contain the flat; these pieces are called the faces of A.
The regions are faces because the whole space is a flat.
The faces of codimension 1 may be called the facets of A.
The face semilattice of an arrangement is the set of all faces, ordered by inclusion. Adding an extra top element to the face semilattice gives the face lattice.
In two dimensions (i.e., in the real affine plane
) each region is a convex polygon
(if it is bounded) or a convex polygonal region which goes off to infinity.
A typical problem about an arrangement in n-dimensional real space is to say how many regions there are, or how many faces of dimension 4, or how many bounded regions. These questions can be answered just from the intersection semilattice. For instance, two basic theorems are that the number of regions of an affine arrangement equals (−1)npA(−1) and the number of bounded regions equals (−1)npA(1). Similarly, the number of k-dimensional faces or bounded faces can be read off as the coefficient of xn−k in (−1)n wA (−x, −1) or (−1)nwA(−x, 1).
designed a fast algorithm to determine the face of an arrangement of hyperplanes containing an input point.
Another question about an arrangement in real space is to decide how many regions are simplices
(the n-dimensional generalization of triangle
s and tetrahedra
). This cannot be answered based solely on the intersection semilattice.
A real linear arrangement has, besides its face semilattice, a poset of regions, a different one for each region. This poset is formed by choosing an arbitrary base region, B0, and associating with each region R the set S(R) consisting of the hyperplanes that separate R from B. The regions are partially ordered so that R1 ≥ R2 if S(R1, R) contains S(R2, R). In the special case when the hyperplanes arise from a root system
, the resulting poset is the corresponding Weyl group
with the weak Bruhat order. In general, the poset of regions is ranked
by the number of separating hyperplanes and its Möbius function
has been computed (Edelman 1984).
affine space (which is hard to visualize because even the complex affine plane has four real dimensions), the complement is connected (all one piece) with holes where the hyperplanes were removed.
A typical problem about an arrangement in complex space is to describe the holes.
The basic theorem about complex arrangements is that the cohomology
of the complement M(A) is completely determined by the intersection semilattice. To be precise, the cohomology ring of M(A) (with integer coefficients) is isomorphic to the Orlik-Solomon algebra on Z.
The isomorphism can be described rather explicitly, and gives a presentation of the cohomology in terms of generators and relations, where generators are represented (in the de Rham cohomology
) as logarithmic differential form
s
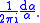
with
any linear form defining the generic hyperplane of the arrangement.
Sometimes one wants to allow repeated hyperplanes in the arrangement. We did not consider this possibility in the preceding discussion, but it makes no material difference.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
and combinatorics
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, an arrangement of hyperplanes is a finite set A of hyperplane
Hyperplane
A hyperplane is a concept in geometry. It is a generalization of the plane into a different number of dimensions.A hyperplane of an n-dimensional space is a flat subset with dimension n − 1...
s in a linear, affine
Affine geometry
In mathematics affine geometry is the study of geometric properties which remain unchanged by affine transformations, i.e. non-singular linear transformations and translations...
, or projective
Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant under projective transformations. This means that, compared to elementary geometry, projective geometry has a different setting, projective space, and a selective set of basic geometric concepts...
space S.
Questions about a hyperplane arrangement A generally concern geometrical, topological, or other properties of the complement, M(A), which is the set that remains when the hyperplanes are removed from the whole space. One may ask how these properties are related to the arrangement and its intersection semilattice.
The intersection semilattice
Semilattice
In mathematics, a join-semilattice is a partially ordered set which has a join for any nonempty finite subset. Dually, a meet-semilattice is a partially ordered set which has a meet for any nonempty finite subset...
of A, written L(A), is the set of all subspaces
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
that are obtained by intersecting some of the hyperplanes; among these subspaces are S itself, all the individual hyperplanes, all intersections of pairs of hyperplanes, etc. (excluding, in the affine case, the empty set). These subspaces are called the flats of A. L(A) is partially ordered by reverse inclusion.
If the whole space S is 2-dimensional, the hyperplanes are line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
s; such an arrangement is often called an arrangement of lines
Arrangement of lines
In geometry an arrangement of lines is the partition of the plane formed by a collection of lines. Bounds on the complexity of arrangements have been studied in discrete geometry, and computational geometers have found algorithms for the efficient construction of arrangements.-Definition:For any...
. Historically, real arrangements of lines were the first arrangements investigated. If S is 3-dimensional one has an arrangement of planes.
The intersection semilattice and the matroid
The intersection semilattice L(A) is a meet semilattice and more specifically is a geometric semilattice.If the arrangement is linear or projective, or if the intersection of all hyperplanes is nonempty, the intersection lattice is a geometric lattice.
(This is why the semilattice must be ordered by reverse inclusion—rather than by inclusion, which might seem more natural but would not yield a geometric (semi)lattice.)
When L(A) is a lattice, the matroid
Matroid
In combinatorics, a branch of mathematics, a matroid or independence structure is a structure that captures the essence of a notion of "independence" that generalizes linear independence in vector spaces....
of A, written M(A), has A for its ground set and has rank function r(S) := codim(I), where S is any subset of A and I is the intersection of the hyperplanes in S. In general, when L(A) is a semilattice, there is an analogous matroid-like structure that might be called a semimatroid, which is a generalization of a matroid (and has the same relationship to the intersection semilattice as does the matroid to the lattice in the lattice case), but is not a matroid if L(A) is not a lattice.
Polynomials
For a subset B of A, let us define f(B) := the intersection of the hyperplanes in B; this is S if B is empty.The characteristic polynomial of A, written pA(y), can be defined by
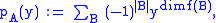
summed over all subsets B of A except, in the affine case, subsets whose intersection is empty. (The dimension of the empty set is defined to be −1.) This polynomial helps to solve some basic questions; see below.
Another polynomial associated with A is the Whitney-number polynomial wA(x, y), defined by
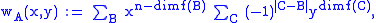
summed over B ⊆ C ⊆ A such that f(B) is nonempty.
Being a geometric lattice or semilattice, L(A) has a characteristic polynomial, pL(A)(y), which has an extensive theory (see matroid). Thus it is good to know that pA(y) = yi pL(A)(y), where i is the smallest dimension of any flat, except that in the projective case it equals yi + 1pL(A)(y).
The Whitney-number polynomial of A is similarly related to that of L(A).
(The empty set is excluded from the semilattice in the affine case specifically so that these relationships will be valid.)
The Orlik–Solomon algebra
The intersection semilattice determines another combinatorial invariant of the arrangement, the Orlik–Solomon algebra. To define it, fix a commutative subring K of the base field, and form the exterior algebra E of the vector space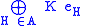generated by the hyperplanes.
A chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
structure is defined on E with the usual boundary operator
.The Orlik-Solomon algebra is then the quotient of E by the ideal
Ideal (ring theory)
In ring theory, a branch of abstract algebra, an ideal is a special subset of a ring. The ideal concept allows the generalization in an appropriate way of some important properties of integers like "even number" or "multiple of 3"....
generated by elements of the form
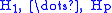(where have an empty intersection) and by boundaries of elements of the same form for which has codimensionCodimension
In mathematics, codimension is a basic geometric idea that applies to subspaces in vector spaces, and also to submanifolds in manifolds, and suitable subsets of algebraic varieties.The dual concept is relative dimension.-Definition:...
less than p.
Real arrangements
In realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
affine space
Affine space
In mathematics, an affine space is a geometric structure that generalizes the affine properties of Euclidean space. In an affine space, one can subtract points to get vectors, or add a vector to a point to get another point, but one cannot add points. In particular, there is no distinguished point...
, the complement is disconnected: it is made up of separate pieces called cells or regions or chambers, each of which is either a bounded region that is a convex
Convex polygon
In geometry, a polygon can be either convex or concave .- Convex polygons :A convex polygon is a simple polygon whose interior is a convex set...
polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
, or an unbounded region that is a convex polyhedral region which goes off to infinity.
Each flat of A is also divided into pieces by the hyperplanes that do not contain the flat; these pieces are called the faces of A.
The regions are faces because the whole space is a flat.
The faces of codimension 1 may be called the facets of A.
The face semilattice of an arrangement is the set of all faces, ordered by inclusion. Adding an extra top element to the face semilattice gives the face lattice.
In two dimensions (i.e., in the real affine plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
) each region is a convex polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
(if it is bounded) or a convex polygonal region which goes off to infinity.
- As an example, if the arrangement consists of three parallel lines, the intersection semilattice consists of the plane and the three lines, but not the empty set. There are four regions, none of them bounded.
- If we add a line crossing the three parallels, then the intersection semilattice consists of the plane, the four lines, and the three points of intersection. There are eight regions, still none of them bounded.
- If we add one more line, parallel to the last, then there are 12 regions, of which two are bounded parallelogramParallelogramIn Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure...
s.
A typical problem about an arrangement in n-dimensional real space is to say how many regions there are, or how many faces of dimension 4, or how many bounded regions. These questions can be answered just from the intersection semilattice. For instance, two basic theorems are that the number of regions of an affine arrangement equals (−1)npA(−1) and the number of bounded regions equals (−1)npA(1). Similarly, the number of k-dimensional faces or bounded faces can be read off as the coefficient of xn−k in (−1)n wA (−x, −1) or (−1)nwA(−x, 1).
designed a fast algorithm to determine the face of an arrangement of hyperplanes containing an input point.
Another question about an arrangement in real space is to decide how many regions are simplices
Simplex
In geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
(the n-dimensional generalization of triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
s and tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
). This cannot be answered based solely on the intersection semilattice.
A real linear arrangement has, besides its face semilattice, a poset of regions, a different one for each region. This poset is formed by choosing an arbitrary base region, B0, and associating with each region R the set S(R) consisting of the hyperplanes that separate R from B. The regions are partially ordered so that R1 ≥ R2 if S(R1, R) contains S(R2, R). In the special case when the hyperplanes arise from a root system
Root system
In mathematics, a root system is a configuration of vectors in a Euclidean space satisfying certain geometrical properties. The concept is fundamental in the theory of Lie groups and Lie algebras...
, the resulting poset is the corresponding Weyl group
Weyl group
In mathematics, in particular the theory of Lie algebras, the Weyl group of a root system Φ is a subgroup of the isometry group of the root system. Specifically, it is the subgroup which is generated by reflections through the hyperplanes orthogonal to the roots, and as such is a finite reflection...
with the weak Bruhat order. In general, the poset of regions is ranked
Ranked poset
In mathematics, a ranked partially ordered set - or poset - may be either:* a graded poset, or* a poset that has the property that for every element x, all maximal chains among those with x as greatest element have the same finite length, or...
by the number of separating hyperplanes and its Möbius function
Incidence algebra
In order theory, a field of mathematics, an incidence algebra is an associative algebra, defined for any locally finite partially ordered setand commutative ring with unity.-Definition:...
has been computed (Edelman 1984).
Complex arrangements
In complexComplex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
affine space (which is hard to visualize because even the complex affine plane has four real dimensions), the complement is connected (all one piece) with holes where the hyperplanes were removed.
A typical problem about an arrangement in complex space is to describe the holes.
The basic theorem about complex arrangements is that the cohomology
Cohomology
In mathematics, specifically in algebraic topology, cohomology is a general term for a sequence of abelian groups defined from a co-chain complex. That is, cohomology is defined as the abstract study of cochains, cocycles, and coboundaries...
of the complement M(A) is completely determined by the intersection semilattice. To be precise, the cohomology ring of M(A) (with integer coefficients) is isomorphic to the Orlik-Solomon algebra on Z.
The isomorphism can be described rather explicitly, and gives a presentation of the cohomology in terms of generators and relations, where generators are represented (in the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
) as logarithmic differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
s
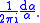
with
any linear form defining the generic hyperplane of the arrangement.Technicalities
Sometimes it is convenient to allow the degenerate hyperplane, which is the whole space S, to belong to an arrangement. If A contains the degenerate hyperplane, then it has no regions because the complement is empty. However, it still has flats, an intersection semilattice, and faces. The preceding discussion assumes the degenerate hyperplane is not in the arrangement.Sometimes one wants to allow repeated hyperplanes in the arrangement. We did not consider this possibility in the preceding discussion, but it makes no material difference.