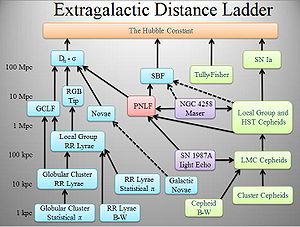
Cosmic distance ladder
Encyclopedia
Astronomy
Astronomy is a natural science that deals with the study of celestial objects and phenomena that originate outside the atmosphere of Earth...
determine the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
s to celestial objects. A real direct distance measurement of an astronomical object is possible only for those objects that are "close enough" (within about a thousand parsecs) to Earth. The techniques for determining distances to more distant objects are all based on various measured correlations between methods that work at close distances with methods that work at larger distances. Several methods rely on a standard candle, which is an astronomical object that has a known luminosity
Luminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
.
The ladder analogy arises because no one technique can measure distances at all ranges encountered in astronomy. Instead, one method can be used to measure nearby distances, a second can be used to measure nearby to intermediate distances, and so on. Each rung of the ladder provides information that can be used to determine the distances at the next higher rung.
Direct measurement

Astrometry
Astrometry is the branch of astronomy that involves precise measurements of the positions and movements of stars and other celestial bodies. The information obtained by astrometric measurements provides information on the kinematics and physical origin of our Solar System and our Galaxy, the Milky...
.
Astronomical unit
Direct distance measurements are based upon precise determination of the distance between the Earth and the Sun, which is called the Astronomical UnitAstronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
(AU). Historically, observations of transits of Venus were crucial in determining the AU; in the first half of the 20th Century, observations of asteroids were also important. Presently the AU is determined with high precision using radar measurements of Venus
Venus
Venus is the second planet from the Sun, orbiting it every 224.7 Earth days. The planet is named after Venus, the Roman goddess of love and beauty. After the Moon, it is the brightest natural object in the night sky, reaching an apparent magnitude of −4.6, bright enough to cast shadows...
and other nearby planets and asteroids, and by tracking interplanetary spacecraft
Spacecraft
A spacecraft or spaceship is a craft or machine designed for spaceflight. Spacecraft are used for a variety of purposes, including communications, earth observation, meteorology, navigation, planetary exploration and transportation of humans and cargo....
in their orbits around the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
through the Solar System
Solar System
The Solar System consists of the Sun and the astronomical objects gravitationally bound in orbit around it, all of which formed from the collapse of a giant molecular cloud approximately 4.6 billion years ago. The vast majority of the system's mass is in the Sun...
. Kepler's Laws
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
provide precise ratio
Ratio
In mathematics, a ratio is a relationship between two numbers of the same kind , usually expressed as "a to b" or a:b, sometimes expressed arithmetically as a dimensionless quotient of the two which explicitly indicates how many times the first number contains the second In mathematics, a ratio is...
s of the sizes of the orbits of objects revolving around the Sun, but not a real measure of the orbits themselves. Radar provides a value in kilometers
Kilometre
The kilometre is a unit of length in the metric system, equal to one thousand metres and is therefore exactly equal to the distance travelled by light in free space in of a second...
for the difference in two orbits' sizes, and from that and the ratio of the two orbit sizes, the size of Earth's orbit comes directly.
Parallax
The most important fundamental distance measurements come from trigonometric parallaxParallax
Parallax is a displacement or difference in the apparent position of an object viewed along two different lines of sight, and is measured by the angle or semi-angle of inclination between those two lines. The term is derived from the Greek παράλλαξις , meaning "alteration"...
. As the Earth orbits around the Sun, the position of nearby stars will appear to shift slightly against the more distant background. These shifts are angles in a right triangle
Triangle
A triangle is one of the basic shapes of geometry: a polygon with three corners or vertices and three sides or edges which are line segments. A triangle with vertices A, B, and C is denoted ....
, with 2 AU
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
making the short leg of the triangle and the distance to the star being the long leg. The amount of shift is quite small, measuring 1 arcseconds for an object at a distance of 1 parsec
Parsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
(3.26 light-years), thereafter decreasing in angular amount as the reciprocal of the distance. Astronomers usually express distances in units of parsecs; light-year
Light-year
A light-year, also light year or lightyear is a unit of length, equal to just under 10 trillion kilometres...
s are used in popular media, but almost invariably values in light-years have been converted from numbers tabulated in parsecs in the original source.
Because parallax becomes smaller for a greater stellar distance, useful distances can be measured only for stars whose parallax is larger than the precision
Accuracy and precision
In the fields of science, engineering, industry and statistics, the accuracy of a measurement system is the degree of closeness of measurements of a quantity to that quantity's actual value. The precision of a measurement system, also called reproducibility or repeatability, is the degree to which...
of the measurement. Parallax measurements typically have an accuracy measured in milliarcseconds. In the 1990s, for example, the Hipparcos
Hipparcos
Hipparcos was a scientific mission of the European Space Agency , launched in 1989 and operated between 1989 and 1993. It was the first space experiment devoted to precision astrometry, the accurate measurement of the positions of celestial objects on the sky...
mission obtained parallaxes for over a hundred thousand stars with a precision of about a milliarcsecond
Minute of arc
A minute of arc, arcminute, or minute of angle , is a unit of angular measurement equal to one sixtieth of one degree. In turn, a second of arc or arcsecond is one sixtieth of one minute of arc....
, providing useful distances for stars out to a few hundred parsecs.
Stars can have a velocity relative to the Sun that causes proper motion
Proper motion
The proper motion of a star is its angular change in position over time as seen from the center of mass of the solar system. It is measured in seconds of arc per year, arcsec/yr, where 3600 arcseconds equal one degree. This contrasts with radial velocity, which is the time rate of change in...
and radial velocity
Radial velocity
Radial velocity is the velocity of an object in the direction of the line of sight . In astronomy, radial velocity most commonly refers to the spectroscopic radial velocity...
. The former is determined by plotting the changing position of the stars over many years, while the latter comes from measuring the Doppler shift in their spectrum caused by motion along the line of sight. For a group of stars with the same spectral class and a similar magnitude range, a mean parallax can be derived from statistical analysis of the proper motions relative to their radial velocities. This statistical parallax method is useful for measuring the distances of bright stars beyond 50 parsecs and giant variable star
Variable star
A star is classified as variable if its apparent magnitude as seen from Earth changes over time, whether the changes are due to variations in the star's actual luminosity, or to variations in the amount of the star's light that is blocked from reaching Earth...
s, including Cepheids and the RR Lyrae variables.
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 A.U. per year, while for halo stars the baseline is 40 A.U. per year. After several decades, the baseline can be orders of magnitude greater than the Earth-Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of other stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the precision is inversely proportion to the square root
Square root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the sample size.
Moving cluster parallax is a technique where the motions of individual stars in a nearby star cluster can be used to find the distance to the cluster. Only open cluster
Open cluster
An open cluster is a group of up to a few thousand stars that were formed from the same giant molecular cloud and have roughly the same age. More than 1,100 open clusters have been discovered within the Milky Way Galaxy, and many more are thought to exist...
s are near enough for this technique to be useful. In particular the distance obtained for the Hyades
Hyades (star cluster)
The Hyades is the nearest open cluster to the Solar System and one of the best-studied of all star clusters. The Hipparcos satellite, the Hubble Space Telescope, and infrared color-magnitude diagram fitting have been used to establish a distance to the cluster's center of ~153 ly...
has been an important step in the distance ladder.
Other individual objects can have fundamental distance estimates made for them under special circumstances. If the expansion of a gas cloud, like a supernova remnant
Supernova remnant
A supernova remnant is the structure resulting from the explosion of a star in a supernova. The supernova remnant is bounded by an expanding shock wave, and consists of ejected material expanding from the explosion, and the interstellar material it sweeps up and shocks along the way.There are two...
or planetary nebula
Planetary nebula
A planetary nebula is an emission nebula consisting of an expanding glowing shell of ionized gas ejected during the asymptotic giant branch phase of certain types of stars late in their life...
, can be observed over time, then an expansion parallax distance to that cloud can be estimated. Binary star
Binary star
A binary star is a star system consisting of two stars orbiting around their common center of mass. The brighter star is called the primary and the other is its companion star, comes, or secondary...
s which are both visual and spectroscopic binaries also can have their distance estimated by similar means. The common characteristic to these is that a measurement of angular motion is combined with a measurement of the absolute velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
(usually obtained via the Doppler effect). The distance estimate comes from computing how far away the object must be to make its observed absolute velocity appear with the observed angular motion.
Expansion parallaxes in particular can give fundamental distance estimates for objects that are very far away, because supernova ejecta have large expansion velocities and large sizes (compared to stars). Further, they can be observed with radio interferometers which can measure very small angular motions. These combine to mean that some supernovae in other galaxies have fundamental distance estimates. Though valuable, such cases are quite rare, so they serve as important consistency checks on the distance ladder rather than workhorse steps by themselves.
Standard candles
Almost all of the physical distance indicators are standard candles. These are objects that belong to some class that have a known brightness. By comparing the known luminosityLuminosity
Luminosity is a measurement of brightness.-In photometry and color imaging:In photometry, luminosity is sometimes incorrectly used to refer to luminance, which is the density of luminous intensity in a given direction. The SI unit for luminance is candela per square metre.The luminosity function...
of the latter to its observed brightness, the distance to the object can be computed using the inverse square law. These objects of known brightness are termed standard candles.
In astronomy, the brightness of an object is given in terms of its absolute magnitude
Absolute magnitude
Absolute magnitude is the measure of a celestial object's intrinsic brightness. it is also the apparent magnitude a star would have if it were 32.6 light years away from Earth...
. This quantity is derived from the logarithm of its luminosity as seen from a distance of 10 parsec
Parsec
The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres ....
s. The apparent magnitude
Apparent magnitude
The apparent magnitude of a celestial body is a measure of its brightness as seen by an observer on Earth, adjusted to the value it would have in the absence of the atmosphere...
, or the magnitude as seen by the observer, can be used to determine the distance D to the object in kiloparsecs (where 1 kpc equals 103 parsecs) as follows:

where m the apparent magnitude and M the absolute magnitude. For this to be accurate, both magnitudes must be in the same frequency band and there can be no relative motion in the radial direction.
Some means of accounting for interstellar extinction, which also makes objects appear fainter and more red, is also needed. The difference between absolute and apparent magnitudes is called the distance modulus
Distance modulus
-Definition:The distance modulus \mu=m-M is the difference between the apparent magnitude m and the absolute magnitude M of an astronomical object...
, and astronomical distances, especially intergalactic ones, are sometimes tabulated in this way.
Problems
Two problems exist for any class of standard candle. The principal one is calibrationCalibration
Calibration is a comparison between measurements – one of known magnitude or correctness made or set with one device and another measurement made in as similar a way as possible with a second device....
, determining exactly what the absolute magnitude of the candle is. This includes defining the class well enough that members can be recognized, and finding enough members with well-known distances that their true absolute magnitude can be determined with enough accuracy. The second lies in recognizing members of the class, and not mistakenly using the standard candle calibration upon an object which does not belong to the class. At extreme distances, which is where one most wishes to use a distance indicator, this recognition problem can be quite serious.
A significant issue with standard candles is the recurring question of how standard they are. For example, all observations seem to indicate that Type Ia supernovae
Type Ia supernova
A Type Ia supernova is a sub-category of supernovae, which in turn are a sub-category of cataclysmic variable stars, that results from the violent explosion of a white dwarf star. A white dwarf is the remnant of a star that has completed its normal life cycle and has ceased nuclear fusion...
that are of known distance have the same brightness (corrected by the shape of the light curve). The basis for this closeness in brightness is discussed below; however, the possibility that the distant Type Ia supernovae have different properties than nearby Type Ia supernovae exists. The use of Type Ia supernovae is crucial in determining the correct cosmological model
Physical cosmology
Physical cosmology, as a branch of astronomy, is the study of the largest-scale structures and dynamics of the universe and is concerned with fundamental questions about its formation and evolution. For most of human history, it was a branch of metaphysics and religion...
. If indeed the properties of Type Ia supernovae are different at large distances, i.e. if the extrapolation of their calibration to arbitrary distances is not valid, ignoring this variation can dangerously bias the reconstruction of the cosmological parameters, in particular the reconstruction of the matter density parameter.
That this is not merely a philosophical issue can be seen from the history of distance measurements using Cepheid variable
Cepheid variable
A Cepheid is a member of a class of very luminous variable stars. The strong direct relationship between a Cepheid variable's luminosity and pulsation period, secures for Cepheids their status as important standard candles for establishing the Galactic and extragalactic distance scales.Cepheid...
s. In the 1950s, Walter Baade
Walter Baade
Wilhelm Heinrich Walter Baade was a German astronomer who worked in the USA from 1931 to 1959.-Biography:He took advantage of wartime blackout conditions during World War II, which reduced light pollution at Mount Wilson Observatory, to resolve stars in the center of the Andromeda galaxy for the...
discovered that the nearby Cepheid variables used to calibrate the standard candle were of a different type than the ones used to measure distances to nearby galaxies. The nearby Cepheid variables were population I stars with much higher metal content than the distant population II stars. As a result, the population II stars were actually much brighter than believed, and this had the effect of doubling the distances to the globular clusters, the nearby galaxies, and the diameter of the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
.
(Another class of physical distance indicator is the standard ruler
Standard ruler
A standard ruler is an astronomical object whose approximate size is known. By measuring its apparent angular diameter in the sky, one can determine its distance from Earth....
. In 2008, galaxy diameters have been proposed as a possible standard ruler for cosmological parameter determination.)
Galactic distance indicators
With few exceptions, distances based on direct measurements are available only out to about a thousand parsecs, which is a modest portion of our own Galaxy. For distances beyond that, measures depend upon physical assumptions, that is, the assertion that one recognizes the object in question, and the class of objects is homogeneous enough that its members can be used for meaningful estimation of distance.Physical distance indicators, used on progressively larger distance scales, include:
- Dynamical parallaxDynamical ParallaxIn astronomy, the distance to a visual binary star may be estimated from the masses of its two components, the size of their orbit, and the period of their revolution around one another...
, using orbital parameters of visual binaries to measure the mass of the system and the mass-luminosity relation to determine the luminosity- Eclipsing binaries — In the last decade, measurement of eclipsing binaries' fundamental parameters has become possible with 8 meter class telescopes. This makes it feasible to use them as indicators of distance. Recently, they have been used to give direct distance estimates to the LMCLarge Magellanic CloudThe Large Magellanic Cloud is a nearby irregular galaxy, and is a satellite of the Milky Way. At a distance of slightly less than 50 kiloparsecs , the LMC is the third closest galaxy to the Milky Way, with the Sagittarius Dwarf Spheroidal and Canis Major Dwarf Galaxy lying closer to the center...
, SMCSmall Magellanic CloudThe Small Magellanic Cloud is a dwarf galaxy. It has a diameter of about 7,000 light-years and contains several hundred million stars. It has a total mass of approximately 7 billion times the mass of our Sun....
, Andromeda GalaxyAndromeda GalaxyThe Andromeda Galaxy is a spiral galaxy approximately 2.5 million light-years from Earth in the constellation Andromeda. It is also known as Messier 31, M31, or NGC 224, and is often referred to as the Great Andromeda Nebula in older texts. Andromeda is the nearest spiral galaxy to the...
and Triangulum GalaxyTriangulum GalaxyThe Triangulum Galaxy is a spiral galaxy approximately 3 million light years from Earth in the constellation Triangulum. It is catalogued as Messier 33 or NGC 598, and is sometimes informally referred to as the Pinwheel Galaxy, a nickname it shares with Messier 101...
. Eclipsing binaries offer a direct method to gauge the distance to galaxies to a new improved 5% level of accuracy which is feasible with current technology up to a distance of around 3 Mpc.
- Eclipsing binaries — In the last decade, measurement of eclipsing binaries' fundamental parameters has become possible with 8 meter class telescopes. This makes it feasible to use them as indicators of distance. Recently, they have been used to give direct distance estimates to the LMC
- RR Lyrae variableRR Lyrae variableRR Lyrae variables are periodic variable stars, commonly found in globular clusters, and often used as standard candles to measure galactic distances.This type of variable is named after the prototype, the variable star RR Lyrae in the constellation Lyra....
s — red giants typically used for measuring distances within the galaxy and in nearby globular clusterGlobular clusterA globular cluster is a spherical collection of stars that orbits a galactic core as a satellite. Globular clusters are very tightly bound by gravity, which gives them their spherical shapes and relatively high stellar densities toward their centers. The name of this category of star cluster is...
s. - The following four indicators all use stars in the old stellar populations (Population II):
- Tip of the red giant branch (TRGB) distance indicator.
- Planetary nebula luminosity functionPlanetary nebula luminosity functionPlanetary nebula luminosity function is a secondary distance indicator used in astronomy. It makes use of the [O III] λ5007 forbidden line found in all planetary nebula which are members of the old stellar populations ....
(PNLF) - Globular cluster luminosity function (GCLF)
- Surface brightness fluctuationSurface brightness fluctuationSurface brightness fluctuation is a secondary distance indicator used to estimate distances to galaxies. The technique uses the fact that galaxies are made up of a finite number of stars. The number of stars in any small patch of the galaxy will vary from point to point, creating a noise-like...
(SBF)
- In galactic astronomy, X-ray burstX-ray bursterX-ray bursters are one class of X-ray binary stars exhibiting periodic and rapid increases in luminosity peaked in the X-ray regime of the electromagnetic spectrum...
s (thermonuclear flashes on the surface of a neutron starNeutron starA neutron star is a type of stellar remnant that can result from the gravitational collapse of a massive star during a Type II, Type Ib or Type Ic supernova event. Such stars are composed almost entirely of neutrons, which are subatomic particles without electrical charge and with a slightly larger...
) are used as standard candles. Observations of X-ray burst sometimes show X-ray spectra indicating radius expansion. Therefore, the X-ray flux at the peak of the burst should correspond to Eddington luminosityEddington luminosityThe Eddington luminosity in a star is defined as the point where the gravitational force inwards equals the continuum radiation force outwards, assuming hydrostatic equilibrium and spherical symmetry. When exceeding the Eddington luminosity, a star would initiate a very intense continuum-driven...
, which can be calculated once the mass of the neutron star is known (1.5 solar masses is a commonly used assumption). This method allows distance determination of some low-mass X-ray binaries. Low-mass X-ray binaries are very faint in the optical, making measuring their distances extremely difficult. - Cepheids and novae
- Individual galaxies in clusters of galaxiesGalaxy groups and clustersGalaxy groups and clusters are the largest known gravitationally bound objects to have arisen thus far in the process of cosmic structure formation. They form the densest part of the large scale structure of the universe...
- The Tully-Fisher relationTully-Fisher relationIn astronomy, the Tully–Fisher relation, published by astronomers R. Brent Tully and J. Richard Fisher in 1977, is an empirical relationship between the intrinsic luminosity of a spiral galaxy and its velocity width...
- The Faber-Jackson relationFaber-Jackson relationThe Faber–Jackson relation is an early empirical power-law relation between the luminosity L and the central stellar velocity dispersion \sigma of elliptical galaxies, first noted by the astronomers Sandra M. Faber and Robert Earl Jackson in 1976...
- Type Ia supernovaType Ia supernovaA Type Ia supernova is a sub-category of supernovae, which in turn are a sub-category of cataclysmic variable stars, that results from the violent explosion of a white dwarf star. A white dwarf is the remnant of a star that has completed its normal life cycle and has ceased nuclear fusion...
e that have a very well-determined maximum absolute magnitude as a function of the shape of their light curveLight curveIn astronomy, a light curve is a graph of light intensity of a celestial object or region, as a function of time. The light is usually in a particular frequency interval or band...
and are useful in determining extragalactic distances up to a few hundred Mpc. A notable exception is SN 2003fg, the "Champagne Supernova", a Type Ia supernova of unusual nature. - RedshiftRedshiftIn physics , redshift happens when light seen coming from an object is proportionally increased in wavelength, or shifted to the red end of the spectrum...
s and Hubble's LawHubble's lawHubble's law is the name for the astronomical observation in physical cosmology that: all objects observed in deep space are found to have a doppler shift observable relative velocity to Earth, and to each other; and that this doppler-shift-measured velocity, of various galaxies receding from...
Main sequence fitting
When the absolute magnitude for a group of stars is plotted against the spectral classification of the star, in a Hertzsprung-Russell diagram, evolutionary patterns are found that relate to the mass, age and composition of the star. In particular, during their hydrogen burning period, stars lie along a curve in the diagram called the main sequenceMain sequence
The main sequence is a continuous and distinctive band of stars that appears on plots of stellar color versus brightness. These color-magnitude plots are known as Hertzsprung–Russell diagrams after their co-developers, Ejnar Hertzsprung and Henry Norris Russell...
. By measuring these properties from a star's spectrum, the position of a main sequence star on the H-R diagram can be determined, and thereby the star's absolute magnitude estimated. A comparison of this value with the apparent magnitude allows the approximate distance to be determined, after correcting for interstellar extinction of the luminosity because of gas and dust.
In a gravitationally-bound star cluster
Star cluster
Star clusters or star clouds are groups of stars. Two types of star clusters can be distinguished: globular clusters are tight groups of hundreds of thousands of very old stars which are gravitationally bound, while open clusters, more loosely clustered groups of stars, generally contain less than...
such as the Hyades
Hyades (star cluster)
The Hyades is the nearest open cluster to the Solar System and one of the best-studied of all star clusters. The Hipparcos satellite, the Hubble Space Telescope, and infrared color-magnitude diagram fitting have been used to establish a distance to the cluster's center of ~153 ly...
, the stars formed at approximately the same age and lie at the same distance. This allows relatively accurate main sequence fitting, providing both age and distance determination.
Extragalactic distance scale
| Method | Uncertainty for Single Galaxy (mag) | Distance to Virgo Cluster Virgo Cluster The Virgo Cluster is a cluster of galaxies whose center is 53.8 ± 0.3 Mly away in the constellation Virgo. Comprising approximately 1300 member galaxies, the cluster forms the heart of the larger Local Supercluster, of which the Local Group is an outlying member... (Mpc Parsec The parsec is a unit of length used in astronomy. It is about 3.26 light-years, or just under 31 trillion kilometres .... ) |
Range (Mpc) |
|---|---|---|---|
| Classical Cepheids | 0.16 | 15 - 25 | 29 |
| Novae | 0.4 | 21.1 ± 3.9 | 20 |
| Planetary Nebula Luminosity Function | 0.3 | 15.4 ± 1.1 | 50 |
| Globular Cluster Luminosity Function | 0.4 | 18.8 ± 3.8 | 50 |
| Surface Brightness Fluctuations | 0.3 | 15.9 ± 0.9 | 50 |
| D - σ relation | 0.5 | 16.8 ± 2.4 | > 100 |
| Type Ia Supernovae | 0.10 | 19.4 ± 5.0 | > 1000 |
The extragalactic distance scale is a series of techniques used today by astronomers to determine the distance of cosmological bodies beyond our own galaxy, which are not easily obtained with traditional methods. Some procedures utilize properties of these objects, such as star
Star
A star is a massive, luminous sphere of plasma held together by gravity. At the end of its lifetime, a star can also contain a proportion of degenerate matter. The nearest star to Earth is the Sun, which is the source of most of the energy on Earth...
s, globular clusters, nebulae, and galaxies as a whole. Other methods are based more on the statistics and probabilities of things such as entire galaxy clusters.
Wilson-Bappu Effect
Discovered in 1956 by Olin Wilson and M.K. Vainu BappuVainu Bappu
Manali Kallat Vainu Bappu was an Indian astronomer and president of the International Astronomical Union. Bappu helped establish several astronomical institutions in India——including the Vainu Bappu Observatory named after him—and also contributed to the establishment of the modern Indian...
, The Wilson-Bappu Effect utilizes the effect known as spectroscopic parallax
Spectroscopic parallax
Spectroscopic parallax is an astronomical method for measuring the distances to stars. Despite its name, it does not rely on the apparent change in the position of the star . This technique can be applied to any main sequence star for which a spectrum can be recorded...
. Certain stars have features in their emission/absorption spectra allowing relatively easy absolute magnitude calculation. Certain spectral lines are directly related to an object's magnitude, such as the K absorption line
Fraunhofer lines
In physics and optics, the Fraunhofer lines are a set of spectral lines named for the German physicist Joseph von Fraunhofer . The lines were originally observed as dark features in the optical spectrum of the Sun....
of calcium. Distance to the star can be calculated from magnitude by the distance modulus
Distance modulus
-Definition:The distance modulus \mu=m-M is the difference between the apparent magnitude m and the absolute magnitude M of an astronomical object...
:

Though in theory this method has the ability to provide reliable distance calculations to stars roughly 7 megaparsecs (Mpc) away, it is generally only used for stars hundreds of kiloparsecs (kpc) away.
This method is only valid for stars over 15 magnitudes.
Classical Cepheids
Beyond the reach of the Wilson-Bappu effectWilson-Bappu effect
The Ca II K line in cool stars is among the strongest absorption lines. A small emission, which originates in the chromosphere, is present in its core. In 1957, Olin C. Wilson and M. K. Vainu Bappu reported on the remarkable correlation between the measured width of the aforementioned emission...
, the next method relies on the period-luminosity relation of classical Cepheid variable stars, first discovered by Henrietta Leavitt. The following relation can be used to calculate the distance to Galactic and extragalactic classical Cepheids:
Several problems complicate the use of Cepheids as standard candles and are actively debated, chief among them are: the nature and linearity of the period-luminosity relation in various passbands and the impact of metallicity on both the zero-point and slope of those relations, and the effects of photometric contamination (blending) and a changing (typically unknown) extinction law on Cepheid distances.
These unresolved matters have resulted in cited values for the Hubble Constant ranging between 60 km/s/Mpc and 80 km/s/Mpc. Resolving this discrepancy is one of the foremost problems in astronomy since the cosmological parameters of the Universe may be constrained by supplying a precise value of the Hubble constant.
Cepheid variable stars were the key instrument in Edwin Hubble’s 1923 conclusion that M31
Andromeda Galaxy
The Andromeda Galaxy is a spiral galaxy approximately 2.5 million light-years from Earth in the constellation Andromeda. It is also known as Messier 31, M31, or NGC 224, and is often referred to as the Great Andromeda Nebula in older texts. Andromeda is the nearest spiral galaxy to the...
(Andromeda) was an external galaxy, as opposed to a smaller nebula within the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
. He was able to calculate the distance of M31 to 285 Kpc, today’s value being 770 Kpc.
As detected thus far, NGC 3370, a spiral galaxy in the constellation Leo, contains the farthest Cepheids yet found at a distance of 29 Mpc. Cepheid variable stars are in no way perfect distance markers: at nearby galaxies they have an error of about 7% and up to a 15% error for the most distant.
Supernovae

Supernova
A supernova is a stellar explosion that is more energetic than a nova. It is pronounced with the plural supernovae or supernovas. Supernovae are extremely luminous and cause a burst of radiation that often briefly outshines an entire galaxy, before fading from view over several weeks or months...
e can be used to measure extragalactic distances, here we cover the most used.
Measuring a supernova's photosphere
We can assume that a supernova expands spherically symmetric. If the supernova is close enough such that we can measure the angular extent, θ(t), of its photospherePhotosphere
The photosphere of an astronomical object is the region from which externally received light originates. The term itself is derived from Ancient Greek roots, φῶς, φωτός/phos, photos meaning "light" and σφαῖρα/sphaira meaning "sphere", in reference to the fact that it is a spheric surface perceived...
, we can use the equation
 .
.Where ω is angular velocity, θ is angular extent. In order to get an accurate measurement, it is necessary to make two observations separated by time Δt. Subsequently, we can use
 .
.Where d is the distance to the supernova, Vej is the supernova's ejecta's radial velocity (it can be assumed that Vej equals Vθ if spherically symmetric).
This method works only if the supernova is close enough to be able to measure accurately the photosphere. Similarly, the expanding shell of gas is in fact not perfectly spherical nor a perfect blackbody. Also interstellar extinction can hinder the accurate measurements of the photosphere. This problem is further exacerbated by core-collapse supernova. All of these factors contribute to the distance error of up to 25%.
Type Ia light curves
Type Ia supernovae are some of the best ways to determine extragalactic distances. Ia's occur when a binary white dwarf star begins to accrete matter from its companion Red Dwarf star. As the white dwarf gains matter, eventually it reaches its Chandrasekhar LimitChandrasekhar limit
When a star starts running out of fuel, it usually cools off and collapses into one of three compact forms, depending on its total mass:* a White Dwarf, a big lump of Carbon and Oxygen atoms, almost like one huge molecule...
of
 .
.Once reached, the star becomes unstable and undergoes a runaway nuclear fusion reaction. Because all Type Ia supernovae explode at about the same mass, their absolute magnitudes are all the same. This makes them very useful as standard candles. All Type Ia supernovae have a standard blue and visual magnitude of

Therefore, when observing a Type Ia supernova, if it is possible to determine what its peak magnitude was, then its distance can be calculated. It is not intrinsically necessary to capture the supernova directly at its peak magnitude; using the multicolor light curve shape method (MLCS), the shape of the light curve (taken at any reasonable time after the initial explosion) is compared to a family of parameterized curves that will determine the absolute magnitude at the maximum brightness. This method also takes into effect interstellar extinction/dimming from dust and gas.
Similarly, the stretch method fits the particular supernovae magnitude light curves to a template light curve. This template, as opposed to being several light curves at different wavelengths (MLCS) is just a single light curve that has been stretched (or compressed) in time. By using this Stretch Factor, the peak magnitude can be determined .
Using Type Ia supernovae is one of the most accurate methods, particularly since supernova explosions can be visible at great distances (their luminosities rival that of the galaxy in which they are situated), much farther than Cepheid Variables (500 times farther). Much time has been devoted to the refining of this method. The current uncertainty approaches a mere 5%, corresponding to an uncertainty of just 0.1 magnitudes.
Novae in distance determinations
NovaNova
A nova is a cataclysmic nuclear explosion in a star caused by the accretion of hydrogen on to the surface of a white dwarf star, which ignites and starts nuclear fusion in a runaway manner...
e can be used in much the same way as supernovae to derive extragalactic distances. There is a direct relation between a nova's max magnitude and the time for its visible light to decline by two magnitudes. This relation is shown to be:

Where
 is the time derivative of the nova's mag, describing the average rate of decline over the first 2 magnitudes.
is the time derivative of the nova's mag, describing the average rate of decline over the first 2 magnitudes.After novae fade, they are about as bright as the most luminous Cepheid Variable stars, therefore both these techniques have about the same max distance: ~ 20 Mpc. The error in this method produces an uncertainty in magnitude of about ± 0.4
Globular cluster luminosity function
Based on the method of comparing the luminosities of globular clusters (located in galactic halos) from distant galaxies to that of the Virgo clusterVirgo Cluster
The Virgo Cluster is a cluster of galaxies whose center is 53.8 ± 0.3 Mly away in the constellation Virgo. Comprising approximately 1300 member galaxies, the cluster forms the heart of the larger Local Supercluster, of which the Local Group is an outlying member...
, the globular cluster luminosity function carries an uncertainty of distance of about 20% (or .4 magnitudes).
US astronomer William Alvin Baum first attempted to use globular clusters to measure distant elliptical galaxies. He compared the brightest globular clusters in Virgo A galaxy with those in Andromeda, assuming the luminosities of the clusters were the same in both. Knowing the distance to Andromeda, has assumed a direct correlation and estimated Virgo A’s distance.
Baum used just a single globular cluster, but individual formations are often poor standard candles. Canadian astronomer Racine assumed the use of the globular cluster luminosity function (GCLF) would lead to a better approximation. The number of globular clusters as a function of magnitude given by:

Where m0 is the turnover magnitude, and M0 the magnitude of the Virgo cluster, sigma the dispersion ~ 1.4 mag.
It is important to remember that it is assumed that globular clusters all have roughly the same luminosities within the universe
Universe
The Universe is commonly defined as the totality of everything that exists, including all matter and energy, the planets, stars, galaxies, and the contents of intergalactic space. Definitions and usage vary and similar terms include the cosmos, the world and nature...
. There is no universal globular cluster luminosity function that applies to all galaxies.
Planetary nebula luminosity function
Like the GCLF method, a similar numerical analysis can be used for planetary nebulae (note the use of more than one!) within far off galaxies. The planetary nebula luminosity functionPlanetary nebula luminosity function
Planetary nebula luminosity function is a secondary distance indicator used in astronomy. It makes use of the [O III] λ5007 forbidden line found in all planetary nebula which are members of the old stellar populations ....
(PNLF) was first proposed in the late 1970s by Holland Cole and David Jenner. They suggested that all planetary nebulae might all have similar maximum intrinsic brightness, now calculated to be M = -4.53. This would therefore make them potential standard candles for determining extragalactic distances.
Astronomer George Howard Jacoby and his fellow colleagues later proposed that the PNLF function equaled:

Where N(M) is number of planetary nebula, having absolute magnitude M. M* is equal to the nebula with the brightest magnitude.
Surface brightness fluctuation method

The surface brightness fluctuation
Surface brightness fluctuation
Surface brightness fluctuation is a secondary distance indicator used to estimate distances to galaxies. The technique uses the fact that galaxies are made up of a finite number of stars. The number of stars in any small patch of the galaxy will vary from point to point, creating a noise-like...
(SBF) method takes advantage of the use of CCD cameras on telescopes. Because of spatial fluctuations in a galaxy’s surface brightness, some pixels on these cameras will pick up more stars than others. However, as distance increases the picture will become increasingly smoother. Analysis of this describes a magnitude of the pixel-to-pixel variation, which is directly related to a galaxy’s distance.
D-σ Relation
The D- σ relation, used in elliptical galaxies, relates the angular diameter (D) of the galaxy to its velocity dispersion. It is important to describe exactly what D represents in order to have a more fitting understanding of this method. It is, more precisely, the galaxy’s angular diameter out to the surface brightness level of 20.75 B-mag arcsec . This surface brightness is independent of the galaxy’s actual distance from us. Instead, D is inversely proportional to the galaxy’s distance, represented as d. So instead of this relation imploring standard candles, instead D provides a standard ruler
. This surface brightness is independent of the galaxy’s actual distance from us. Instead, D is inversely proportional to the galaxy’s distance, represented as d. So instead of this relation imploring standard candles, instead D provides a standard rulerStandard ruler
A standard ruler is an astronomical object whose approximate size is known. By measuring its apparent angular diameter in the sky, one can determine its distance from Earth....
. This relation between D and σ is

Where C is a constant which depends on the distance to the galaxy clusters.
This method has the possibility of become one of the strongest methods of galactic distance calculators, perhaps exceeding the range of even the Tully-Fisher method. As of today, however, elliptical galaxies aren’t bright enough to provide a calibration for this method through the use of techniques such as Cepheids. So instead calibration is done using more crude methods.
Overlap and scaling
A succession of distance indicators, which is the distance ladder, is needed for determining distances to other galaxies. The reason is that objects bright enough to be recognized and measured at such distances are so rare that few or none are present nearby, so there are too few examples close enough with reliable trigonometric parallax to calibrate the indicator. For example, Cepheid variables, one of the best indicators for nearby spiral galaxiesSpiral galaxy
A spiral galaxy is a certain kind of galaxy originally described by Edwin Hubble in his 1936 work The Realm of the Nebulae and, as such, forms part of the Hubble sequence. Spiral galaxies consist of a flat, rotating disk containing stars, gas and dust, and a central concentration of stars known as...
, cannot be satisfactorily calibrated by parallax alone. The situation is further complicated by the fact that different stellar populations generally do not have all types of stars in them. Cepheids in particular are massive stars, with short lifetimes, so they will only be found in places where stars have very recently been formed. Consequently, because elliptical galaxies
Elliptical galaxy
An elliptical galaxy is a galaxy having an approximately ellipsoidal shape and a smooth, nearly featureless brightness profile. They range in shape from nearly spherical to highly flat and in size from hundreds of millions to over one trillion stars...
usually have long ceased to have large-scale star formation, they will not have Cepheids. Instead, distance indicators whose origins are in an older stellar population (like novae and RR Lyrae variables) must be used. However, RR Lyrae variables are less luminous than Cepheids (so they cannot be seen as far away as Cepheids can), and novae are unpredictable and an intensive monitoring program — and luck during that program — is needed to gather enough novae in the target galaxy for a good distance estimate.
Because the more distant steps of the cosmic distance ladder depend upon the nearer ones, the more distant steps include the effects of error
Error
The word error entails different meanings and usages relative to how it is conceptually applied. The concrete meaning of the Latin word "error" is "wandering" or "straying". Unlike an illusion, an error or a mistake can sometimes be dispelled through knowledge...
s in the nearer steps, both systematic and statistical ones. The result of these propagating errors
Propagation of uncertainty
In statistics, propagation of error is the effect of variables' uncertainties on the uncertainty of a function based on them...
means that distances in astronomy are rarely known to the same level of precision as measurements in the other sciences, and that the precision necessarily is poorer for more distant types of object.
Another concern, especially for the very brightest standard candles, is their "standardness": how homogeneous the objects are in their true absolute magnitude. For some of these different standard candles, the homogeneity is based on theories about the formation
Star formation
Star formation is the process by which dense parts of molecular clouds collapse into a ball of plasma to form a star. As a branch of astronomy star formation includes the study of the interstellar medium and giant molecular clouds as precursors to the star formation process and the study of young...
and evolution
Stellar evolution
Stellar evolution is the process by which a star undergoes a sequence of radical changes during its lifetime. Depending on the mass of the star, this lifetime ranges from only a few million years to trillions of years .Stellar evolution is not studied by observing the life of a single...
of stars and galaxies, and is thus also subject to uncertainties in those aspects. For the most luminous of distance indicators, the Type Ia supernovae, this homogeneity is known to be poor ; however, no other class of object is bright enough to be detected at such large distances, so the class is useful simply because there is no real alternative.
The observational result of Hubble's Law, the proportional
Proportionality (mathematics)
In mathematics, two variable quantities are proportional if one of them is always the product of the other and a constant quantity, called the coefficient of proportionality or proportionality constant. In other words, are proportional if the ratio \tfrac yx is constant. We also say that one...
relationship between distance and the speed with which a galaxy is moving away from us (usually referred to as redshift
Redshift
In physics , redshift happens when light seen coming from an object is proportionally increased in wavelength, or shifted to the red end of the spectrum...
) is a product of the cosmic distance ladder. Hubble
Edwin Hubble
Edwin Powell Hubble was an American astronomer who profoundly changed the understanding of the universe by confirming the existence of galaxies other than the Milky Way - our own galaxy...
observed that fainter galaxies are more redshifted. Finding the value of the Hubble constant was the result of decades of work by many astronomers, both in amassing the measurements of galaxy redshifts and in calibrating the steps of the distance ladder. Hubble's Law is the primary means we have for estimating the distances of quasar
Quasar
A quasi-stellar radio source is a very energetic and distant active galactic nucleus. Quasars are extremely luminous and were first identified as being high redshift sources of electromagnetic energy, including radio waves and visible light, that were point-like, similar to stars, rather than...
s and distant galaxies in which individual distance indicators cannot be seen.
See also
- Distance measures (cosmology)Distance measures (cosmology)Distance measures are used in physical cosmology to give a natural notion of the distance between two objects or events in the universe. They are often used to tie some observable quantity to another quantity that is not directly...
- Standard rulerStandard rulerA standard ruler is an astronomical object whose approximate size is known. By measuring its apparent angular diameter in the sky, one can determine its distance from Earth....
- Orders of magnitude (length)#Astronomical
Further reading
- An Introduction to Modern Astrophysics, Carroll and Ostlie, copyright 2007
- Measuring the Universe The Cosmological Distance Ladder, Stephen Webb, copyright 2001
- The Cosmos, Pasachoff and Filippenko, copyright 2007
- The Astrophysical Journal, The Globular Cluster Luminosity Function as a Distance Indicator: Dynamical Effects, Ostriker and Gnedin, May 5, 1997


