D'Alembert's paradox
Encyclopedia
In fluid dynamics
, d'Alembert's paradox (or the hydrodynamic paradox) is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert
. D'Alembert proved that – for incompressible and inviscid
potential flow
– the drag force
is zero on a body moving with constant velocity
relative to the fluid
. Zero drag is in direct contradiction to the observation of substantial drag on bodies moving relative to fluids, such as air and water; especially at high velocities corresponding with high Reynolds numbers.
D’Alembert, working on a 1749 Prize Problem of the Berlin Academy on flow drag, concluded: "It seems to me that the theory (potential flow), developed in all possible rigor, gives, at least in several cases, a strictly vanishing resistance, a singular paradox which I leave to future Geometers to elucidate". A physical paradox
indicates flaws in the theory.
Fluid mechanics was thus discredited by engineers from the start, which resulted in an unfortunate split – between the field of hydraulics
, observing phenomena which could not be explained, and theoretical fluid mechanics
explaining phenomena which could not be observed – in the words of the Chemistry Nobel Laureate Sir Cyril Hinshelwood
.
According to scientific consensus
, the occurrence of the paradox is due to neglect of the effects of viscosity
. In conjunction with scientific experiments, there were huge advances in the theory of viscous fluid friction during the 19th century. With respect to the paradox, this culminated in the discovery and description of thin boundary layer
s by Ludwig Prandtl in 1904. Even at very high Reynolds numbers, the thin boundary layers remain as a result of viscous forces. These viscous forces cause friction drag on streamlined objects, and for bluff bodies the additional result is flow separation
and a low-pressure wake
behind the object, leading to form drag.
The general view in the fluid mechanics community is that, from a practical point of view, the paradox is solved along the lines suggested by Prandtl. A formal mathematical proof is lacking, and difficult to provide, as in so many other fluid-flow problems involving the Navier–Stokes equations (which are used to describe viscous flow).
, who modelled viscous
fluid friction. Saint-Venant states in 1847:
Soon after, in 1851, Stokes
calculated the drag on a sphere in Stokes flow, known as Stokes' law
. Stokes flow is the low Reynolds-number limit of the Navier–Stokes equations describing the motion of a viscous liquid.
However, when the flow problem is put into a non-dimensional form
, the viscous Navier–Stokes equations converge for increasing Reynolds numbers towards the inviscid Euler equations, suggesting that the flow should converge towards the inviscid solutions of potential flow
theory – having the zero drag of the d'Alembert paradox. Of this, there is no evidence found in experimental measurements of drag and flow visualisations. This again raised questions concerning the applicability of fluid mechanics in the second half of the 19th century.
In the second half of the 19th century, focus shifted again towards using inviscid flow
theory for the description of fluid drag—assuming that viscosity becomes less important at high Reynolds numbers. The model proposed by Kirchhoff
and Rayleigh
was based on the free-streamline theory of Helmholtz
and consists of a steady wake
behind the body. Assumptions applied to the wake region include: flow velocities equal to the body velocity, and a constant pressure. This wake region is separated—from the potential flow outside the body and wake—by vortex
sheets with discontinuous jumps in the tangent
ial velocity across the interface.
In order to have a non-zero drag on the body, the wake region must extend to infinity. This condition is indeed fulfilled for the Kirchhoff flow perpendicular to a plate. The theory correctly states the drag force to be proportional to the square of the velocity.
In first instance, the theory could only be applied to flows separating at sharp edges. Later, in 1907, it was extended by Levi-Civita
to flows separating from a smooth curved boundary.
It was readily known that such steady flows are not stable, since the vortex sheets develop so-called Kelvin–Helmholtz instabilities. But this steady-flow model was studied further in the hope it still could give a reasonable estimate of drag. Rayleigh asks "... whether the calculations of resistance are materially affected by this circumstance as the pressures experienced must be nearly independent of what happens at some distance in the rear of the obstacle, where the instability would first begin to manifest itself."
However, fundamental objections arose against this approach: Kelvin
observed that if a plate is moving with constant velocity through the fluid, the velocity in the wake is equal to that of the plate. The infinite extent of the wake—widening with the distance from the plate, as obtained from the theory—results in an infinite kinetic energy in the wake, which must be rejected on physical grounds.
Moreover, the observed pressure differences between front and back of the plate, and resulting drag forces, are much larger than predicted: for a flat plate perpendicular to the flow the predicted drag coefficient
is CD=0.88, while in experiments CD=2.0 is found. This is mainly due to suction at the wake side of the plate, induced by the unsteady flow in the real wake (as opposed to the theory which assumes a constant flow velocity equal to the plate's velocity).
So, this theory is found to be unsatisfactory as an explanation of drag on a body moving through a fluid. Although it can be applied to so-called cavity flows where, instead of a wake filled with fluid, a vacuum cavity is assumed to exist behind the body.
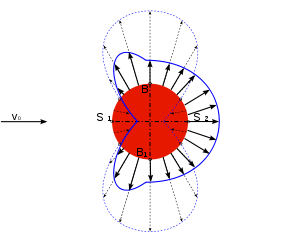The German physicist Ludwig Prandtl suggested in 1904 that the effects of a thin viscous boundary layer
possibly could be the source of substantial drag. Prandtl put forward the idea that, at high velocities and high Reynolds numbers, a no-slip boundary condition causes a strong variation of the flow speeds over a thin layer near the wall of the body. This leads to the generation of vorticity and viscous dissipation
of kinetic energy
in the boundary layer. The energy dissipation, which is lacking in the inviscid theories, results for bluff bodies in separation
of the flow. The low pressure in the wake
region causes form drag, and this can be larger than the friction drag due to the viscous shear stress
at the wall.
Evidence that Prandtl's scenario occurs for bluff bodies in flows of high Reynolds numbers can be seen in impulsively started flows around a cylinder. Initially the flow resembles potential flow, after which the flow separates near the rear stagnation point
. Thereafter, the separation points move upstream, resulting in a low-pressure region of separated flow.
Prandtl made the hypothesis that the viscous effects are important in thin layers – called boundary layers – adjacent to solid boundaries, and that viscosity
has no role of importance outside. The boundary-layer thickness
becomes smaller when the viscosity reduces. The full problem of viscous flow, described by the non-linear Navier–Stokes equations, is in general not mathematically solvable. However, using his hypothesis (and backed up by experiments) Prandtl was able to derive an approximate model for the flow inside the boundary layer, called boundary-layer theory; while the flow outside the boundary layer could be treated using inviscid flow
theory. Boundary-layer theory is amenable to the method of matched asymptotic expansions
for deriving approximate solutions. In the simplest case of a flat plate parallel to the incoming flow, boundary-layer theory results in (friction) drag, whereas all inviscid flow theories will predict zero drag. Importantly for aeronautics
, Prandtl's theory can be applied directly to streamlined bodies like airfoil
s where, in addition to surface-friction drag, there is also form drag. Form drag is due to the effect of the boundary layer and thin wake on the pressure
distribution around the airfoil.
may be very difficult.
The mathematician Garrett Birkhoff
in the opening chapter of his book Hydrodynamics from 1950, addresses a number of paradoxes of fluid mechanics (including d'Alembert's paradox) and expresses a clear doubt in their official resolutions:
In particular, on d'Alembert's paradox, he considers another possible route to the creation of drag: instability of the potential flow solutions to the Euler equations
. Birkhoff states:
In his 1951 review of Birkhoff's book, the mathematician James J. Stoker
sharply criticizes the first chapter of the book:
In the second and revised edition of Birkhoff's Hydrodynamics in 1960, the above two statements no longer appear.
The importance and usefulness of the achievements, made on the subject of the d'Alembert paradox, are reviewed by Stewartson thirty years later. His long 1981 survey article starts with:
For many paradoxes in physics, their resolution often lies in transcending the available theory. In the case of d'Alembert's paradox, the essential mechanism for its resolution was provided by Prandtl through the discovery and modelling of thin viscous boundary layer
s – which are non-vanishing at high Reynolds numbers.
, inviscid
and irrotational.
An inviscid fluid is described by the Euler equations
, which for an incompressible flow read
where u denotes the flow velocity
of the fluid, p the pressure
, ρ the density
, and ∇ is the gradient
operator. The assumption that the flow is irrotational means that the velocity satisfies ∇ × u = 0.
Hence, we have
where the first equality is a vector calculus identity and the second equality uses that the flow is irrotational. Furthermore, for every irrotational flow, there exists a velocity potential φ such that u = ∇φ. Substituting this all in the equation for momentum conservation yields
Thus, the quantity between brackets must be constant (any t-dependence can be eliminated by redefining φ). Assuming that the fluid is at rest at infinity and that the pressure is defined to be zero there, this constant is zero, and thus
which is the Bernoulli equation
for unsteady potential flow.
Since u = ∇φ, this can be integrated with respect to x:
The force F that the fluid exerts on the body is given by the surface integral
where A denotes the body surface and n the normal vector on the body surface. But it follows from (2) that
thus
with the contribution of R(t) to the integral being equal to zero.
At this point, it becomes more convenient to work in the vector components. The kth component of this equation reads
Let V be the volume occupied by the fluid. The divergence theorem
says that
The right-hand side is an integral over an infinite volume, so this needs some justification, which can be provided by appealing to potential theory to show that the velocity u must fall off as r−3 – corresponding to a dipole
potential field in case of a three-dimensional body of finite extent – where r is the distance to the centre of the body. The integrand in the volume integral can be rewritten as follows:
where first equality (1) and then the incompressibility of the flow are used. Substituting this back into the volume integral and another application of the divergence theorem again. This yields
Substituting this in (3), we find that
The fluid cannot penetrate the body and thus n · u = n · v on the body surface. Thus,
Finally, the drag is the force in the direction in which the body moves, so
Hence the drag vanishes. This is d'Alembert's paradox.
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, d'Alembert's paradox (or the hydrodynamic paradox) is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
. D'Alembert proved that – for incompressible and inviscid
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
– the drag force
Drag (physics)
In fluid dynamics, drag refers to forces which act on a solid object in the direction of the relative fluid flow velocity...
is zero on a body moving with constant velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
relative to the fluid
Fluid
In physics, a fluid is a substance that continually deforms under an applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas and, to some extent, plastic solids....
. Zero drag is in direct contradiction to the observation of substantial drag on bodies moving relative to fluids, such as air and water; especially at high velocities corresponding with high Reynolds numbers.
D’Alembert, working on a 1749 Prize Problem of the Berlin Academy on flow drag, concluded: "It seems to me that the theory (potential flow), developed in all possible rigor, gives, at least in several cases, a strictly vanishing resistance, a singular paradox which I leave to future Geometers to elucidate". A physical paradox
Physical paradox
A physical paradox is an apparent contradiction in physical descriptions of the universe. While many physical paradoxes have accepted resolutions, others defy resolution and may indicate flaws in theory...
indicates flaws in the theory.
Fluid mechanics was thus discredited by engineers from the start, which resulted in an unfortunate split – between the field of hydraulics
Hydraulics
Hydraulics is a topic in applied science and engineering dealing with the mechanical properties of liquids. Fluid mechanics provides the theoretical foundation for hydraulics, which focuses on the engineering uses of fluid properties. In fluid power, hydraulics is used for the generation, control,...
, observing phenomena which could not be explained, and theoretical fluid mechanics
Fluid mechanics
Fluid mechanics is the study of fluids and the forces on them. Fluid mechanics can be divided into fluid statics, the study of fluids at rest; fluid kinematics, the study of fluids in motion; and fluid dynamics, the study of the effect of forces on fluid motion...
explaining phenomena which could not be observed – in the words of the Chemistry Nobel Laureate Sir Cyril Hinshelwood
Cyril Norman Hinshelwood
Sir Cyril Norman Hinshelwood OM PRS was an English physical chemist.Born in London, his parents were Norman Macmillan Hinshelwood, a chartered accountant, and Ethe Frances née Smith. He was educated first in Canada, returning in 1905 on the death of his father to a small flat in Chelsea where he...
.
According to scientific consensus
Scientific consensus
Scientific consensus is the collective judgment, position, and opinion of the community of scientists in a particular field of study. Consensus implies general agreement, though not necessarily unanimity. Scientific consensus is not by itself a scientific argument, and it is not part of the...
, the occurrence of the paradox is due to neglect of the effects of viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
. In conjunction with scientific experiments, there were huge advances in the theory of viscous fluid friction during the 19th century. With respect to the paradox, this culminated in the discovery and description of thin boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
s by Ludwig Prandtl in 1904. Even at very high Reynolds numbers, the thin boundary layers remain as a result of viscous forces. These viscous forces cause friction drag on streamlined objects, and for bluff bodies the additional result is flow separation
Flow separation
All solid objects travelling through a fluid acquire a boundary layer of fluid around them where viscous forces occur in the layer of fluid close to the solid surface. Boundary layers can be either laminar or turbulent...
and a low-pressure wake
Wake
A wake is the region of recirculating flow immediately behind a moving or stationary solid body, caused by the flow of surrounding fluid around the body.-Fluid dynamics:...
behind the object, leading to form drag.
The general view in the fluid mechanics community is that, from a practical point of view, the paradox is solved along the lines suggested by Prandtl. A formal mathematical proof is lacking, and difficult to provide, as in so many other fluid-flow problems involving the Navier–Stokes equations (which are used to describe viscous flow).
Viscous friction: Saint-Venant, Navier and Stokes
First steps towards solving the paradox were made by Saint-VenantAdhémar Jean Claude Barré de Saint-Venant
Adhémar Jean Claude Barré de Saint-Venant was a mechanician and mathematician who contributed to early stress analysis and also developed the one-dimensional unsteady open channel flow shallow water equations or Saint-Venant equations that are a fundamental set of equations used in modern...
, who modelled viscous
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
fluid friction. Saint-Venant states in 1847:
- "But one finds another result if, instead of an ideal fluid – object of the calculations of the geometers of the last century – one uses a real fluid, composed of a finite number of molecules and exerting in its state of motion unequal pressure forces or forces having components tangential to the surface elements through which they act; components to which we refer as the friction of the fluid, a name which has been given to them since Descartes and Newton until Venturi."
Soon after, in 1851, Stokes
George Gabriel Stokes
Sir George Gabriel Stokes, 1st Baronet FRS , was an Irish mathematician and physicist, who at Cambridge made important contributions to fluid dynamics , optics, and mathematical physics...
calculated the drag on a sphere in Stokes flow, known as Stokes' law
Stokes' law
In 1851, George Gabriel Stokes derived an expression, now known as Stokes' law, for the frictional force – also called drag force – exerted on spherical objects with very small Reynolds numbers in a continuous viscous fluid...
. Stokes flow is the low Reynolds-number limit of the Navier–Stokes equations describing the motion of a viscous liquid.
However, when the flow problem is put into a non-dimensional form
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
, the viscous Navier–Stokes equations converge for increasing Reynolds numbers towards the inviscid Euler equations, suggesting that the flow should converge towards the inviscid solutions of potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
theory – having the zero drag of the d'Alembert paradox. Of this, there is no evidence found in experimental measurements of drag and flow visualisations. This again raised questions concerning the applicability of fluid mechanics in the second half of the 19th century.
Inviscid separated flow: Kirchhoff and Rayleigh
Inviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
theory for the description of fluid drag—assuming that viscosity becomes less important at high Reynolds numbers. The model proposed by Kirchhoff
Gustav Kirchhoff
Gustav Robert Kirchhoff was a German physicist who contributed to the fundamental understanding of electrical circuits, spectroscopy, and the emission of black-body radiation by heated objects...
and Rayleigh
John Strutt, 3rd Baron Rayleigh
John William Strutt, 3rd Baron Rayleigh, OM was an English physicist who, with William Ramsay, discovered the element argon, an achievement for which he earned the Nobel Prize for Physics in 1904...
was based on the free-streamline theory of Helmholtz
Hermann von Helmholtz
Hermann Ludwig Ferdinand von Helmholtz was a German physician and physicist who made significant contributions to several widely varied areas of modern science...
and consists of a steady wake
Wake
A wake is the region of recirculating flow immediately behind a moving or stationary solid body, caused by the flow of surrounding fluid around the body.-Fluid dynamics:...
behind the body. Assumptions applied to the wake region include: flow velocities equal to the body velocity, and a constant pressure. This wake region is separated—from the potential flow outside the body and wake—by vortex
Vortex
A vortex is a spinning, often turbulent,flow of fluid. Any spiral motion with closed streamlines is vortex flow. The motion of the fluid swirling rapidly around a center is called a vortex...
sheets with discontinuous jumps in the tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
ial velocity across the interface.
In order to have a non-zero drag on the body, the wake region must extend to infinity. This condition is indeed fulfilled for the Kirchhoff flow perpendicular to a plate. The theory correctly states the drag force to be proportional to the square of the velocity.
In first instance, the theory could only be applied to flows separating at sharp edges. Later, in 1907, it was extended by Levi-Civita
Tullio Levi-Civita
Tullio Levi-Civita, FRS was an Italian mathematician, most famous for his work on absolute differential calculus and its applications to the theory of relativity, but who also made significant contributions in other areas. He was a pupil of Gregorio Ricci-Curbastro, the inventor of tensor calculus...
to flows separating from a smooth curved boundary.
It was readily known that such steady flows are not stable, since the vortex sheets develop so-called Kelvin–Helmholtz instabilities. But this steady-flow model was studied further in the hope it still could give a reasonable estimate of drag. Rayleigh asks "... whether the calculations of resistance are materially affected by this circumstance as the pressures experienced must be nearly independent of what happens at some distance in the rear of the obstacle, where the instability would first begin to manifest itself."
However, fundamental objections arose against this approach: Kelvin
William Thomson, 1st Baron Kelvin
William Thomson, 1st Baron Kelvin OM, GCVO, PC, PRS, PRSE, was a mathematical physicist and engineer. At the University of Glasgow he did important work in the mathematical analysis of electricity and formulation of the first and second laws of thermodynamics, and did much to unify the emerging...
observed that if a plate is moving with constant velocity through the fluid, the velocity in the wake is equal to that of the plate. The infinite extent of the wake—widening with the distance from the plate, as obtained from the theory—results in an infinite kinetic energy in the wake, which must be rejected on physical grounds.
Moreover, the observed pressure differences between front and back of the plate, and resulting drag forces, are much larger than predicted: for a flat plate perpendicular to the flow the predicted drag coefficient
Drag coefficient
In fluid dynamics, the drag coefficient is a dimensionless quantity that is used to quantify the drag or resistance of an object in a fluid environment such as air or water. It is used in the drag equation, where a lower drag coefficient indicates the object will have less aerodynamic or...
is CD=0.88, while in experiments CD=2.0 is found. This is mainly due to suction at the wake side of the plate, induced by the unsteady flow in the real wake (as opposed to the theory which assumes a constant flow velocity equal to the plate's velocity).
So, this theory is found to be unsatisfactory as an explanation of drag on a body moving through a fluid. Although it can be applied to so-called cavity flows where, instead of a wake filled with fluid, a vacuum cavity is assumed to exist behind the body.
Thin boundary layers: Prandtl
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
possibly could be the source of substantial drag. Prandtl put forward the idea that, at high velocities and high Reynolds numbers, a no-slip boundary condition causes a strong variation of the flow speeds over a thin layer near the wall of the body. This leads to the generation of vorticity and viscous dissipation
Dissipation
In physics, dissipation embodies the concept of a dynamical system where important mechanical models, such as waves or oscillations, lose energy over time, typically from friction or turbulence. The lost energy converts into heat, which raises the temperature of the system. Such systems are called...
of kinetic energy
Kinetic energy
The kinetic energy of an object is the energy which it possesses due to its motion.It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its acceleration, the body maintains this kinetic energy unless its speed changes...
in the boundary layer. The energy dissipation, which is lacking in the inviscid theories, results for bluff bodies in separation
Flow separation
All solid objects travelling through a fluid acquire a boundary layer of fluid around them where viscous forces occur in the layer of fluid close to the solid surface. Boundary layers can be either laminar or turbulent...
of the flow. The low pressure in the wake
Wake
A wake is the region of recirculating flow immediately behind a moving or stationary solid body, caused by the flow of surrounding fluid around the body.-Fluid dynamics:...
region causes form drag, and this can be larger than the friction drag due to the viscous shear stress
Shear stress
A shear stress, denoted \tau\, , is defined as the component of stress coplanar with a material cross section. Shear stress arises from the force vector component parallel to the cross section...
at the wall.
Evidence that Prandtl's scenario occurs for bluff bodies in flows of high Reynolds numbers can be seen in impulsively started flows around a cylinder. Initially the flow resembles potential flow, after which the flow separates near the rear stagnation point
Stagnation point
In fluid dynamics, a stagnation point is a point in a flow field where the local velocity of the fluid is zero. Stagnation points exist at the surface of objects in the flow field, where the fluid is brought to rest by the object...
. Thereafter, the separation points move upstream, resulting in a low-pressure region of separated flow.
Prandtl made the hypothesis that the viscous effects are important in thin layers – called boundary layers – adjacent to solid boundaries, and that viscosity
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
has no role of importance outside. The boundary-layer thickness
Boundary-layer thickness
This page describes some parameters used to measure the properties of boundary layers. Consider a stationary body with a turbulent flow moving around it, like the semi-infinite flat plate with air flowing over the top of the plate...
becomes smaller when the viscosity reduces. The full problem of viscous flow, described by the non-linear Navier–Stokes equations, is in general not mathematically solvable. However, using his hypothesis (and backed up by experiments) Prandtl was able to derive an approximate model for the flow inside the boundary layer, called boundary-layer theory; while the flow outside the boundary layer could be treated using inviscid flow
Inviscid flow
In fluid dynamics there are problems that are easily solved by using the simplifying assumption of an ideal fluid that has no viscosity. The flow of a fluid that is assumed to have no viscosity is called inviscid flow....
theory. Boundary-layer theory is amenable to the method of matched asymptotic expansions
Method of matched asymptotic expansions
In mathematics, particularly in solving singularly perturbed differential equations, the method of matched asymptotic expansions is a common approach to finding an accurate approximation to a problem's solution.-Method overview:...
for deriving approximate solutions. In the simplest case of a flat plate parallel to the incoming flow, boundary-layer theory results in (friction) drag, whereas all inviscid flow theories will predict zero drag. Importantly for aeronautics
Aeronautics
Aeronautics is the science involved with the study, design, and manufacturing of airflight-capable machines, or the techniques of operating aircraft and rocketry within the atmosphere...
, Prandtl's theory can be applied directly to streamlined bodies like airfoil
Airfoil
An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....
s where, in addition to surface-friction drag, there is also form drag. Form drag is due to the effect of the boundary layer and thin wake on the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
distribution around the airfoil.
Open questions
To verify, as Prandtl suggested, that a vanishingly small cause (vanishingly small viscosity for increasing Reynolds number) has a large effect – substantial drag —may be very difficult.
The mathematician Garrett Birkhoff
Garrett Birkhoff
Garrett Birkhoff was an American mathematician. He is best known for his work in lattice theory.The mathematician George Birkhoff was his father....
in the opening chapter of his book Hydrodynamics from 1950, addresses a number of paradoxes of fluid mechanics (including d'Alembert's paradox) and expresses a clear doubt in their official resolutions:
- "
In particular, on d'Alembert's paradox, he considers another possible route to the creation of drag: instability of the potential flow solutions to the Euler equations
Euler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
. Birkhoff states:
- "
In his 1951 review of Birkhoff's book, the mathematician James J. Stoker
James J. Stoker
James Johnston Stoker was an American applied mathematician and engineer. He was director of the Courant Institute of Mathematical Sciences and is considered one of the founders of the institute, Courant and Friedrichs being the others. Stoker is known for his work in differential geometry and...
sharply criticizes the first chapter of the book:
- "
In the second and revised edition of Birkhoff's Hydrodynamics in 1960, the above two statements no longer appear.
The importance and usefulness of the achievements, made on the subject of the d'Alembert paradox, are reviewed by Stewartson thirty years later. His long 1981 survey article starts with:
- "
For many paradoxes in physics, their resolution often lies in transcending the available theory. In the case of d'Alembert's paradox, the essential mechanism for its resolution was provided by Prandtl through the discovery and modelling of thin viscous boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
s – which are non-vanishing at high Reynolds numbers.
Zero drag in potential flow
Potential flow
The three main assumptions in the derivation of d'Alembert's paradox is that the flow is incompressibleIncompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
, inviscid
Viscosity
Viscosity is a measure of the resistance of a fluid which is being deformed by either shear or tensile stress. In everyday terms , viscosity is "thickness" or "internal friction". Thus, water is "thin", having a lower viscosity, while honey is "thick", having a higher viscosity...
and irrotational.
An inviscid fluid is described by the Euler equations
Euler equations
In fluid dynamics, the Euler equations are a set of equations governing inviscid flow. They are named after Leonhard Euler. The equations represent conservation of mass , momentum, and energy, corresponding to the Navier–Stokes equations with zero viscosity and heat conduction terms. Historically,...
, which for an incompressible flow read
where u denotes the flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
of the fluid, p the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
, ρ the density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
, and ∇ is the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
operator. The assumption that the flow is irrotational means that the velocity satisfies ∇ × u = 0.
Hence, we have
where the first equality is a vector calculus identity and the second equality uses that the flow is irrotational. Furthermore, for every irrotational flow, there exists a velocity potential φ such that u = ∇φ. Substituting this all in the equation for momentum conservation yields
Thus, the quantity between brackets must be constant (any t-dependence can be eliminated by redefining φ). Assuming that the fluid is at rest at infinity and that the pressure is defined to be zero there, this constant is zero, and thus
which is the Bernoulli equation
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
for unsteady potential flow.
Zero drag
Now, suppose that a body moves with constant velocity v through the fluid, which is at rest infinitely far away. Then the velocity field of the fluid has to follow the body, so it is of the form u(x, t) = u(x − v t, 0), and thus:Since u = ∇φ, this can be integrated with respect to x:
The force F that the fluid exerts on the body is given by the surface integral
where A denotes the body surface and n the normal vector on the body surface. But it follows from (2) that
thus
with the contribution of R(t) to the integral being equal to zero.
At this point, it becomes more convenient to work in the vector components. The kth component of this equation reads
Let V be the volume occupied by the fluid. The divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
says that
The right-hand side is an integral over an infinite volume, so this needs some justification, which can be provided by appealing to potential theory to show that the velocity u must fall off as r−3 – corresponding to a dipole
Dipole
In physics, there are several kinds of dipoles:*An electric dipole is a separation of positive and negative charges. The simplest example of this is a pair of electric charges of equal magnitude but opposite sign, separated by some distance. A permanent electric dipole is called an electret.*A...
potential field in case of a three-dimensional body of finite extent – where r is the distance to the centre of the body. The integrand in the volume integral can be rewritten as follows:
where first equality (1) and then the incompressibility of the flow are used. Substituting this back into the volume integral and another application of the divergence theorem again. This yields
Substituting this in (3), we find that
The fluid cannot penetrate the body and thus n · u = n · v on the body surface. Thus,
Finally, the drag is the force in the direction in which the body moves, so
Hence the drag vanishes. This is d'Alembert's paradox.
External links
- Potential Flow and d'Alembert's Paradox at MathPages