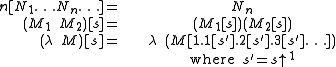De Bruijn index
Encyclopedia
In mathematical logic
, the De Bruijn index is a notation invented by the Dutch
mathematician
Nicolaas Govert de Bruijn
for representing terms in the λ calculus with the purpose of eliminating the names of the variable from the notation. Terms written using these indexes are invariant with respect to α conversion, so the check for α-equivalence is the same as that for syntactic equality. Each De Bruijn index is a natural number
that represents an occurrence of a variable
in a λ-term, and denotes the number of binders that are in scope
between that occurrence and its corresponding binder. The following are some examples:
De Bruijn indexes are commonly used in higher-order
reasoning systems such as automated theorem prover
s and logic programming
systems.
where n — natural number
s greater than 0 — are the variables. A variable n is bound if it is in the scope of at least n binders (λ); otherwise it is free. The binding site for a variable n is the nth binder it is in the scope
of, starting from the innermost binder.
The most primitive operation on λ-terms is substitution: replacing free variables in a term with other terms. In the β-reduction (λ M) N, for example, we must:
To illustrate, consider the application) (λ 5 1)
which might correspond to the following term written in the usual notation) (λx. w x).
After step 1, we obtain the term λ 4 □ (λ 1 □), where the variables that are substituted for are replaced with boxes. Step 2 lowers the free variables, giving λ 3 □ (λ 1 □). Finally, in step 3 we replace the boxes with the argument; the first box is under one binder, so we replace it with λ 6 1 (which is λ 5 1 with the free variables increased by 1); the second is under two binders, so we replace it with λ 7 1. The final result is λ 3 (λ 6 1) (λ 1 (λ 7 1)).
Formally, a substitution is an unbounded list of term replacements for the free variables, written M1.M2…, where Mi is the replacement for the ith free variable. The increasing operation in step 3 is sometimes called shift and written ↑k where k is a natural number indicating the amount to increase the variables; For example, ↑0 is the identity substitution, leaving a term unchanged.
The application of a substitution s to a term M is written M[s]. The composition of two substitutions s1 and s2 is written s1 s2 and defined by
The rules for application are as follows:
The steps outlined for the β-reduction above are thus more concisely expressed as: N →β M [N.1.2.3…].
is one such approach where α-conversion is applied as needed to ensure that:
In practice this is cumbersome, inefficient, and often error-prone. It has therefore led to the search for different representations of such terms. On the other hand, the named representation of λ-terms is more pervasive and can be more immediately understandable by others because the variables can be given descriptive names. Thus, even if a system uses De Bruijn indexes internally, it will present a user interface with names.
De Bruijn indexes are not the only representation of λ-terms that obviates the problem of α-conversion. Among named representations, the nominal
approaches of Pitts and Gabbay is one approach, where the representation of a λ-term is treated as an equivalence class of all terms rewritable
to it using variable permutations. This approach is taken by the Nominal Datatype Package of Isabelle/HOL
.
Another common alternative is an appeal to higher-order representation
s where the λ-binder is treated as a true function. In such representations, the issues of α-equivalence, substitution, etc. are identified with the same operations in a meta-logic.
When reasoning about the meta-theoretic properties of a deductive system in a proof assistant, it is sometimes desirable to limit oneself to first-order representations and to have the ability to (re)name assumptions. The locally nameless approach uses a mixed representation of variables—De Bruijn indexes for bound variables and names for free variables—that is able to benefit from the α-canonical form of De Bruijn indexed terms when appropriate.
Mathematical logic
Mathematical logic is a subfield of mathematics with close connections to foundations of mathematics, theoretical computer science and philosophical logic. The field includes both the mathematical study of logic and the applications of formal logic to other areas of mathematics...
, the De Bruijn index is a notation invented by the Dutch
Netherlands
The Netherlands is a constituent country of the Kingdom of the Netherlands, located mainly in North-West Europe and with several islands in the Caribbean. Mainland Netherlands borders the North Sea to the north and west, Belgium to the south, and Germany to the east, and shares maritime borders...
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn
Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....
for representing terms in the λ calculus with the purpose of eliminating the names of the variable from the notation. Terms written using these indexes are invariant with respect to α conversion, so the check for α-equivalence is the same as that for syntactic equality. Each De Bruijn index is a natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
that represents an occurrence of a variable
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
in a λ-term, and denotes the number of binders that are in scope
Scope (programming)
In computer programming, scope is an enclosing context where values and expressions are associated. Various programming languages have various types of scopes. The type of scope determines what kind of entities it can contain and how it affects them—or semantics...
between that occurrence and its corresponding binder. The following are some examples:
- The term λx. λy. x, sometimes called the K combinator, is written as λ λ 2 with De Bruijn indexes. The binder for the occurrence x is the second λ in scope.
- The term λx. λy. λz. x z (y z) (the S combinator), with De Bruijn indexes, is λ λ λ 3 1 (2 1).
- The term λz. (λy. y (λx. x)) (λx. z x) is λ (λ 1 (λ 1)) (λ 2 1). See the following illustration, where the binders are coloured and the references are shown with arrows.
De Bruijn indexes are commonly used in higher-order
Higher-order logic
In mathematics and logic, a higher-order logic is a form of predicate logic that is distinguished from first-order logic by additional quantifiers and a stronger semantics...
reasoning systems such as automated theorem prover
Automated theorem proving
Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...
s and logic programming
Logic programming
Logic programming is, in its broadest sense, the use of mathematical logic for computer programming. In this view of logic programming, which can be traced at least as far back as John McCarthy's [1958] advice-taker proposal, logic is used as a purely declarative representation language, and a...
systems.
Formal definition
Formally, λ-terms (M, N, …) written using De Bruijn indexes have the following syntax (parentheses allowed freely):- M, N, … ::= n | M N | λ M
where n — natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s greater than 0 — are the variables. A variable n is bound if it is in the scope of at least n binders (λ); otherwise it is free. The binding site for a variable n is the nth binder it is in the scope
Scope (programming)
In computer programming, scope is an enclosing context where values and expressions are associated. Various programming languages have various types of scopes. The type of scope determines what kind of entities it can contain and how it affects them—or semantics...
of, starting from the innermost binder.
The most primitive operation on λ-terms is substitution: replacing free variables in a term with other terms. In the β-reduction (λ M) N, for example, we must:
- find the variables n1, n2, …, nk in M that are bound by the λ in λ M,
- decrease the free variables of
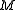to match the removal of the outer 
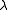-binder, and - replace n1, n2, …, nk with N, suitably increasing the free variables occurring in N each time, to match the number of λ-binders the corresponding variable occurs under when substituted.
To illustrate, consider the application) (λ 5 1)
which might correspond to the following term written in the usual notation) (λx. w x).
After step 1, we obtain the term λ 4 □ (λ 1 □), where the variables that are substituted for are replaced with boxes. Step 2 lowers the free variables, giving λ 3 □ (λ 1 □). Finally, in step 3 we replace the boxes with the argument; the first box is under one binder, so we replace it with λ 6 1 (which is λ 5 1 with the free variables increased by 1); the second is under two binders, so we replace it with λ 7 1. The final result is λ 3 (λ 6 1) (λ 1 (λ 7 1)).
Formally, a substitution is an unbounded list of term replacements for the free variables, written M1.M2…, where Mi is the replacement for the ith free variable. The increasing operation in step 3 is sometimes called shift and written ↑k where k is a natural number indicating the amount to increase the variables; For example, ↑0 is the identity substitution, leaving a term unchanged.
The application of a substitution s to a term M is written M[s]. The composition of two substitutions s1 and s2 is written s1 s2 and defined by
- M [s1 s2] = (M [s1]) [s2].
The rules for application are as follows:
The steps outlined for the β-reduction above are thus more concisely expressed as: N →β M [N.1.2.3…].
Alternatives to De Bruijn indexes
When using the standard "named" representation of λ-terms, where variables are treated as labels or strings, one has to explicitly handle α-conversion when defining any operation on the terms. The standard Variable Convention of BarendregtHenk Barendregt
Hendrik Pieter Barendregt is a Dutch logician, known for his work in lambda calculus and type theory.Barendregt studied mathematical logic at Utrecht University, obtaining his Masters in 1968 and his Ph.D. in 1971, both cum laude, under Dirk van Dalen and Georg Kreisel...
is one such approach where α-conversion is applied as needed to ensure that:
- bound variables are distinct from free variables, and
- all binders bind variables not already in scope.
In practice this is cumbersome, inefficient, and often error-prone. It has therefore led to the search for different representations of such terms. On the other hand, the named representation of λ-terms is more pervasive and can be more immediately understandable by others because the variables can be given descriptive names. Thus, even if a system uses De Bruijn indexes internally, it will present a user interface with names.
De Bruijn indexes are not the only representation of λ-terms that obviates the problem of α-conversion. Among named representations, the nominal
Nominal techniques
Nominal techniques are a range of techniques, based on nominal sets, for handling names and binding, e.g. in abstract syntax. Research into nominal sets gave rise to nominal terms, a metalanguage for embedding object languages with name binding constructs into....
approaches of Pitts and Gabbay is one approach, where the representation of a λ-term is treated as an equivalence class of all terms rewritable
Rewriting
In mathematics, computer science, and logic, rewriting covers a wide range of methods of replacing subterms of a formula with other terms. What is considered are rewriting systems...
to it using variable permutations. This approach is taken by the Nominal Datatype Package of Isabelle/HOL
Isabelle theorem prover
The Isabelle theorem prover is an interactive theorem prover, successor of the Higher Order Logic theorem prover. It is an LCF-style theorem prover , so it is based on a small logical core guaranteeing logical correctness...
.
Another common alternative is an appeal to higher-order representation
Higher-order abstract syntax
In computer science, higher-order abstract syntax is a technique for the representation of abstract syntax trees for languages with variable binders.-Relation to first-order abstract syntax:...
s where the λ-binder is treated as a true function. In such representations, the issues of α-equivalence, substitution, etc. are identified with the same operations in a meta-logic.
When reasoning about the meta-theoretic properties of a deductive system in a proof assistant, it is sometimes desirable to limit oneself to first-order representations and to have the ability to (re)name assumptions. The locally nameless approach uses a mixed representation of variables—De Bruijn indexes for bound variables and names for free variables—that is able to benefit from the α-canonical form of De Bruijn indexed terms when appropriate.
See also
- The De Bruijn notationDe Bruijn notationIn mathematical logic, the De Bruijn notation is a syntax for terms in the λ calculus invented by the Dutch mathematician Nicolaas Govert de Bruijn...
for λ-terms. This notation has little to do with De Bruijn indexes, but the name "De Bruijn notation" is often (erroneously) used to stand for it.