
Higher-order abstract syntax
Encyclopedia
In computer science
, higher-order abstract syntax (abbreviated HOAS) is a technique for the representation of abstract syntax trees for languages with variable binders
.
that has certain structure by its very nature. For instance, in first-order abstract syntax (FOAS) trees, as commonly used in compiler
s, the tree structure implies the subexpression relation, meaning that no parentheses are required to disambiguate programs (as they are in the concrete syntax). HOAS exposes additional structure: the relationship between variables and their binding sites. In FOAS representations, a variable is typically represented with an identifier, with the relation between binding site and use being indicated by using the same identifier. With HOAS, there is no name for the variable; each use of the variable refers directly to the binding site.
There are a number of reasons why this technique is useful. First, it makes the binding structure of a program explicit: just as there is no need to explain operator precedence in a FOAS representation, there is no need to have the rules of binding and scope at hand to interpret a HOAS representation. Second, programs that are
alpha-equivalent
(differing only in the names of bound variables) have identical representations in HOAS, which can make equivalence checking more efficient.
where variables are associated with their binding sites via edges. Another popular way to implement HOAS (in, for example, compilers) is with de Bruijn indices
.
to encode the binding structure of the object language
.
For instance, the logical framework LF
has a λ-construct, which has arrow
(→) type. A first-order encoding of an object language construct
syntax):
exp : type.
var : type.
v : var -> exp.
let : exp -> var -> exp -> exp.
Here,
The canonical
HOAS representation of the same object language would be:
exp : type.
let : exp -> (exp -> exp) -> exp.
In this representation, object level variables do not appear explicitly. The constant
(the body of the let). This function is the higher-order part: an expression with a free variable is
represented as an expression with holes that are filled in by the meta-level function when applied. As a concrete example, we would construct the object level expression
let x = 1 + 2
in x + 3
(assuming the natural constructors for numbers and addition) using the HOAS signature above as
let (plus 1 2) ([y] plus y 3)
where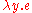 .
.
This specific representation has advantages beyond the ones above: for one, by reusing the meta-level notion of binding, the encoding enjoys properties such as type-preserving substitution without the need to define/prove them. In this way using HOAS can drastically reduce the amount of boilerplate code having to do with binding in an encoding.
Because this technique reuses the mechanism of the meta-language to encode a concept in the object language, it is generally only applicable when the meta-language and object-language notions of binding coincide. This is often the case, but not always: for instance, it is unlikely that a HOAS encoding of dynamic scope such as in Lisp
would be possible in a statically-scoped
language like LF.
Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, higher-order abstract syntax (abbreviated HOAS) is a technique for the representation of abstract syntax trees for languages with variable binders
Name binding
In programming languages, name binding is the association of objects with identifiers. An identifier bound to an object is said to reference that object. Machine languages have no built-in notion of identifiers, but name-object bindings as a service and notation for the programmer is implemented...
.
Relation to first-order abstract syntax
An abstract syntax tree is abstract because it is a mathematical objectMathematical object
In mathematics and the philosophy of mathematics, a mathematical object is an abstract object arising in mathematics.Commonly encountered mathematical objects include numbers, permutations, partitions, matrices, sets, functions, and relations...
that has certain structure by its very nature. For instance, in first-order abstract syntax (FOAS) trees, as commonly used in compiler
Compiler
A compiler is a computer program that transforms source code written in a programming language into another computer language...
s, the tree structure implies the subexpression relation, meaning that no parentheses are required to disambiguate programs (as they are in the concrete syntax). HOAS exposes additional structure: the relationship between variables and their binding sites. In FOAS representations, a variable is typically represented with an identifier, with the relation between binding site and use being indicated by using the same identifier. With HOAS, there is no name for the variable; each use of the variable refers directly to the binding site.
There are a number of reasons why this technique is useful. First, it makes the binding structure of a program explicit: just as there is no need to explain operator precedence in a FOAS representation, there is no need to have the rules of binding and scope at hand to interpret a HOAS representation. Second, programs that are
alpha-equivalent
Lambda calculus
In mathematical logic and computer science, lambda calculus, also written as λ-calculus, is a formal system for function definition, function application and recursion. The portion of lambda calculus relevant to computation is now called the untyped lambda calculus...
(differing only in the names of bound variables) have identical representations in HOAS, which can make equivalence checking more efficient.
Implementation
One mathematical object that could be used to implement HOAS is a graphGraph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
where variables are associated with their binding sites via edges. Another popular way to implement HOAS (in, for example, compilers) is with de Bruijn indices
De Bruijn index
In mathematical logic, the De Bruijn index is a notation invented by the Dutch mathematician Nicolaas Govert de Bruijn for representing terms in the λ calculus with the purpose of eliminating the names of the variable from the notation. Terms written using these indexes are invariant with respect...
.
Use in logical frameworks
In the domain of logical frameworks, the term higher-order abstract syntax is usually used to refer to a specific representation that uses the binders of the meta-languageMetalanguage
Broadly, any metalanguage is language or symbols used when language itself is being discussed or examined. In logic and linguistics, a metalanguage is a language used to make statements about statements in another language...
to encode the binding structure of the object language
Object language
An object language is a language which is the "object" of study in various fields including logic, linguistics, mathematics and theoretical computer science. The language being used to talk about an object language is called a metalanguage...
.
For instance, the logical framework LF
LF (logical framework)
In logic, a logical framework provides a means to define a logic as a signature in a higher-order type theory in such a way that provability of a formula in the original logic reduces to a type inhabitation problem in the framework type theory. This approach has been used successfully for ...
has a λ-construct, which has arrow
(→) type. A first-order encoding of an object language construct
let would be (using TwelfTwelf
Twelf is an implementation of the logical framework LF. It is used for logic programming and for the formalization of programming language theory.-Introduction:...
syntax):
exp : type.
var : type.
v : var -> exp.
let : exp -> var -> exp -> exp.
Here,
exp is the family of object language expressions. The family var is the representation of variables (implemented perhaps as natural numbers, which is not shown); the constant v witnesses the fact that variables are expressions. The constant let is an expression that takes three arguments: an expression (that is being bound), a variable (that it is bound to) and another expression (that the variable is bound within).The canonical
Canonical
Canonical is an adjective derived from canon. Canon comes from the greek word κανών kanon, "rule" or "measuring stick" , and is used in various meanings....
HOAS representation of the same object language would be:
exp : type.
let : exp -> (exp -> exp) -> exp.
In this representation, object level variables do not appear explicitly. The constant
let takes an expression (that is being bound) and a meta-level function exp → exp(the body of the let). This function is the higher-order part: an expression with a free variable is
represented as an expression with holes that are filled in by the meta-level function when applied. As a concrete example, we would construct the object level expression
let x = 1 + 2
in x + 3
(assuming the natural constructors for numbers and addition) using the HOAS signature above as
let (plus 1 2) ([y] plus y 3)
where
[y] e is Twelf's syntax for the function 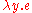 .
.This specific representation has advantages beyond the ones above: for one, by reusing the meta-level notion of binding, the encoding enjoys properties such as type-preserving substitution without the need to define/prove them. In this way using HOAS can drastically reduce the amount of boilerplate code having to do with binding in an encoding.
Because this technique reuses the mechanism of the meta-language to encode a concept in the object language, it is generally only applicable when the meta-language and object-language notions of binding coincide. This is often the case, but not always: for instance, it is unlikely that a HOAS encoding of dynamic scope such as in Lisp
Lisp programming language
Lisp is a family of computer programming languages with a long history and a distinctive, fully parenthesized syntax. Originally specified in 1958, Lisp is the second-oldest high-level programming language in widespread use today; only Fortran is older...
would be possible in a statically-scoped
language like LF.

