Debye length
Encyclopedia
In plasma physics, the Debye length (also called Debye radius), named after the Dutch physicist and physical chemist Peter Debye
, is the scale over which mobile charge carriers (e.g. electrons) screen out electric fields
in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge separation can occur. A Debye sphere is a volume whose radius is the Debye length, in which there is a sphere of influence, and outside of which charges are screened. The notion of Debye length plays an important role in plasma physics, electrolytes and colloids (DLVO theory
).
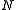different species of charges, the 
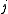-th species carries charge 
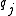and has concentration 
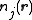at position 
. According to the so-called "primitive model", these charges are distributed in a continuous medium that is characterized only by its relative static permittivity, 
.
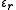This distribution of charges within this medium gives rise to an electric potential
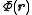that satisfies Poisson's equation
:
,
where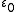
is the electric constant
.
The mobile charges not only establish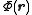
but also move in response to the associated Coulomb force
,
.
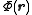If we further assume the system to be in thermodynamic equilibrium
with a heat bath at absolute temperature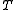
, then the
concentrations of discrete charges,
, may be considered to be
thermodynamic (ensemble) averages and the associated electric potential
to be
a thermodynamic mean field
.
With these assumptions, the concentration of the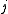
-th charge species is described
by the Boltzmann distribution
,
,
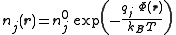where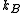
is Boltzmann's constant and where 
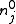is the mean
concentration of charges of species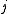
.
Identifying the instantaneous concentrations
and potential in the Poisson equation with their mean-field counterparts in Boltzmann's distribution
yields the Poisson-Boltzmann equation
:
.
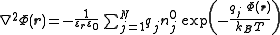Solutions to this nonlinear equation are known for some simple systems. Solutions for more general
systems may be obtained in the high-temperature (weak coupling) limit,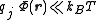
, by Taylor expanding the exponential:
.
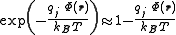This approximation yields the linearized Poisson-Boltzmann equation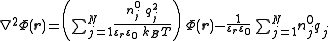
which also is known as the Debye-Hückel equation
:
The second term on the right-hand side vanishes for systems that are electrically neutral. The term in parentheses has the units of an inverse length squared and by
dimensional analysis
leads to the definition of the characteristic length scale
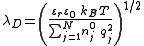
that commonly is referred to as the Debye-Hückel length. As the only characteristic length scale in the Debye-Hückel equation,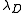
sets the scale for variations in the potential and in the concentrations of charged species. All charged species contribute to the Debye-Hückel length in the same way, regardless of the sign of their charges.
The Debye-Hückel length may be expressed in terms of the Bjerrum length
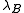as
,
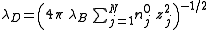where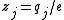
is the integer charge number that relates the charge on the 
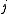-th ionic
species to the elementary charge
.
Source: Chapter 19: The Particle Kinetics of Plasma
http://www.pma.caltech.edu/Courses/ph136/yr2004/
Hannes Alfven
pointed out that: "In a low density plasma, localized space charge regions may build up large potential
drops over distances of the order of some tens of the Debye lengths. Such regions have been called electric double layers. An electric double layer
is the simplest space charge distribution that gives a potential drop in the layer and a vanishing electric field on each side of the layer. In the laboratory, double layers have been studied for half a century, but their importance in cosmic plasmas has not been generally recognized."
(
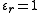), and the Debye length is
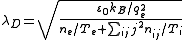
where
The ion term is often dropped, giving
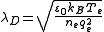
although this is only valid when the mobility of ions is negligible compared to the process's timescale.
or a colloidal dispersion, the Debye length is usually denoted with symbol κ−1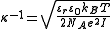
where
or, for a symmetric monovalent electrolyte,
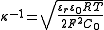
where
Alternatively,
where
For water at room temperature, λB ≈ 0.7 nm.
At room temperature (25 °C), one can consider in water the relation :
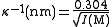
where
The Debye length of silicon
is given:
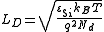
where
When doping profiles exceed the Debye length, majority carriers no longer behave according to the distribution of the dopants. Instead, a measure of the profile of the doping gradients provides an “effective” profile that better matches the profile of the majority carrier density.
Peter Debye
Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...
, is the scale over which mobile charge carriers (e.g. electrons) screen out electric fields
Electric field screening
Screening is the damping of electric fields caused by the presence of mobile charge carriers. It is an important part of the behavior of charge-carrying fluids, such as ionized gases and conduction electrons in semiconductors and metals....
in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge separation can occur. A Debye sphere is a volume whose radius is the Debye length, in which there is a sphere of influence, and outside of which charges are screened. The notion of Debye length plays an important role in plasma physics, electrolytes and colloids (DLVO theory
DLVO theory
The DLVO theory is named after Derjaguin and Landau, Verwey and Overbeek.The theory describes the force between charged surfaces interacting through a liquid medium....
).
Physical origin
The Debye length arises naturally in the thermodynamic description of large systems of mobile charges. In a system of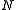 different species of charges, the 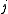-th species carries charge 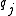and has concentration 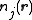at position . According to the so-called "primitive model", these charges are distributed in a continuous medium that is characterized only by its relative static permittivity, 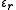.This distribution of charges within this medium gives rise to an electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
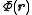that satisfies Poisson's equationPoisson's equation
In mathematics, Poisson's equation is a partial differential equation of elliptic type with broad utility in electrostatics, mechanical engineering and theoretical physics...
:
,where
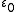is the electric constantElectric constant
The physical constant ε0, commonly called the vacuum permittivity, permittivity of free space or electric constant is an ideal, physical constant, which is the value of the absolute dielectric permittivity of classical vacuum...
.
The mobile charges not only establish
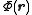but also move in response to the associated Coulomb forceCoulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
,
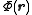.If we further assume the system to be in thermodynamic equilibrium
Thermodynamic equilibrium
In thermodynamics, a thermodynamic system is said to be in thermodynamic equilibrium when it is in thermal equilibrium, mechanical equilibrium, radiative equilibrium, and chemical equilibrium. The word equilibrium means a state of balance...
with a heat bath at absolute temperature
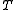, then theconcentrations of discrete charges,
, may be considered to bethermodynamic (ensemble) averages and the associated electric potential
Electric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
to be
a thermodynamic mean field
Mean field theory
Mean field theory is a method to analyse physical systems with multiple bodies. A many-body system with interactions is generally very difficult to solve exactly, except for extremely simple cases . The n-body system is replaced by a 1-body problem with a chosen good external field...
.
With these assumptions, the concentration of the
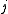-th charge species is describedby the Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
,
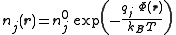,where
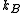is Boltzmann's constant and where 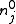is the meanconcentration of charges of species
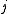.Identifying the instantaneous concentrations
and potential in the Poisson equation with their mean-field counterparts in Boltzmann's distribution
yields the Poisson-Boltzmann equation
Poisson-Boltzmann equation
The Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913...
:
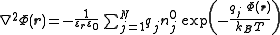.Solutions to this nonlinear equation are known for some simple systems. Solutions for more general
systems may be obtained in the high-temperature (weak coupling) limit,
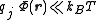, by Taylor expanding the exponential: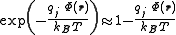.This approximation yields the linearized Poisson-Boltzmann equation
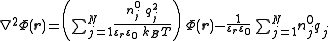
which also is known as the Debye-Hückel equation
Debye-Hückel equation
The Debye–Hückel equation and Debye–Hückel limiting law, were derived by Peter Debye and Erich Hückel, who developed a theory with which to calculate activity coefficients of electrolyte solutions. Activities, rather than concentrations, are needed in many chemical calculations because solutions...
:
The second term on the right-hand side vanishes for systems that are electrically neutral. The term in parentheses has the units of an inverse length squared and by
dimensional analysis
Dimensional analysis
In physics and all science, dimensional analysis is a tool to find or check relations among physical quantities by using their dimensions. The dimension of a physical quantity is the combination of the basic physical dimensions which describe it; for example, speed has the dimension length per...
leads to the definition of the characteristic length scale
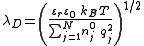
that commonly is referred to as the Debye-Hückel length. As the only characteristic length scale in the Debye-Hückel equation,
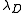sets the scale for variations in the potential and in the concentrations of charged species. All charged species contribute to the Debye-Hückel length in the same way, regardless of the sign of their charges.The Debye-Hückel length may be expressed in terms of the Bjerrum length
Bjerrum length
The Bjerrum length is the separation at which the electrostatic interaction between twoelementary charges is comparable in magnitude to the thermal energy scale,...
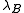as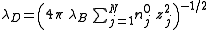,where
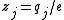is the integer charge number that relates the charge on the 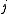-th ionicspecies to the elementary charge
Elementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
.Typical values
In space plasmas where the electron density is relatively low, the Debye length may reach macroscopic values, such as in the magnetosphere, solar wind, interstellar medium and intergalactic medium (see table):| Plasma | Density ne(m-3) | Electron temperature T(K) | Magnetic field B(T) | Debye length λD(m) |
| Solar core | 1032 | 107 | -- | 10−11 |
| Tokamak | 1020 | 108 | 10 | 10−4 |
| Gas discharge | 1016 | 104 | -- | 10−4 |
| Ionosphere | 1012 | 103 | 10−5 | 10−3 |
| Magnetosphere | 107 | 107 | 10−8 | 102 |
| Solar wind | 106 | 105 | 10−9 | 10 |
| Interstellar medium | 105 | 104 | 10−10 | 10 |
| Intergalactic medium | 1 | 106 | -- | 105 |
http://www.pma.caltech.edu/Courses/ph136/yr2004/
Hannes Alfven
Hannes Alfvén
Hannes Olof Gösta Alfvén was a Swedish electrical engineer, plasma physicist and winner of the 1970 Nobel Prize in Physics for his work on magnetohydrodynamics . He described the class of MHD waves now known as Alfvén waves...
pointed out that: "In a low density plasma, localized space charge regions may build up large potential
drops over distances of the order of some tens of the Debye lengths. Such regions have been called electric double layers. An electric double layer
Double layer (plasma)
A double layer is a structure in a plasma and consists of two parallel layers with opposite electrical charge. The sheets of charge cause a strong electric field and a correspondingly sharp change in voltage across the double layer. Ions and electrons which enter the double layer are accelerated,...
is the simplest space charge distribution that gives a potential drop in the layer and a vanishing electric field on each side of the layer. In the laboratory, double layers have been studied for half a century, but their importance in cosmic plasmas has not been generally recognized."
Debye length in a plasma
In a plasma, the background medium may be treated as the vacuum(
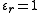), and the Debye length is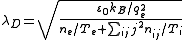where
- λD is the Debye length,
- ε0 is the permittivity of free space,
- kB is the Boltzmann constant,
- qe is the charge of an electron,
- Te and Ti are the temperatures of the electrons and ions, respectively,
- ne is the density of electrons,
- nijis the density of atomic species i, with positive ionIonAn ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
ic charge jqe
The ion term is often dropped, giving
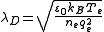
although this is only valid when the mobility of ions is negligible compared to the process's timescale.
Debye length in an electrolyte
In an electrolyteElectrolyte
In chemistry, an electrolyte is any substance containing free ions that make the substance electrically conductive. The most typical electrolyte is an ionic solution, but molten electrolytes and solid electrolytes are also possible....
or a colloidal dispersion, the Debye length is usually denoted with symbol κ−1
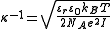
where
- I is the ionic strengthIonic strengthThe ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
of the electrolyte, and here the unit should be mole/m3, - ε0 is the permittivity of free space,
- εr is the dielectric constant,
- kB is the Boltzmann constant,
- T is the absolute temperature in kelvinKelvinThe kelvin is a unit of measurement for temperature. It is one of the seven base units in the International System of Units and is assigned the unit symbol K. The Kelvin scale is an absolute, thermodynamic temperature scale using as its null point absolute zero, the temperature at which all...
s, - NA is the Avogadro number.
- e is the elementary chargeElementary chargeThe elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
,
or, for a symmetric monovalent electrolyte,
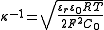
where
- R is the gas constantGas constantThe gas constant is a physical constant which is featured in many fundamental equations in the physical sciences, such as the ideal gas law and the Nernst equation. It is equivalent to the Boltzmann constant, but expressed in units of energy The gas constant (also known as the molar, universal,...
, - F is the Faraday constant,
- C0 is the molar concentration of the electrolyte.
Alternatively,
where
-
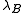is the Bjerrum lengthBjerrum lengthThe Bjerrum length is the separation at which the electrostatic interaction between twoelementary charges is comparable in magnitude to the thermal energy scale,...
of the medium.
For water at room temperature, λB ≈ 0.7 nm.
At room temperature (25 °C), one can consider in water the relation :
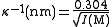
where
- κ−1 is expressed in nanometers (nm)
- I is the ionic strengthIonic strengthThe ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
expressed in molar (M or mol/L)
Debye length in silicon
The Debye length has become increasingly significant in the modeling of solid state devices as improvements in lithographic technologies have enabled smaller geometries.The Debye length of silicon
Silicon
Silicon is a chemical element with the symbol Si and atomic number 14. A tetravalent metalloid, it is less reactive than its chemical analog carbon, the nonmetal directly above it in the periodic table, but more reactive than germanium, the metalloid directly below it in the table...
is given:
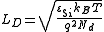
where
- εSi is the dielectric constant of silicon,
- kB is the Boltzmann's constant,
- T is the absolute temperature in kelvins,
- q is the elementary charge, and
- Nd is the density of donors in a substrate.
When doping profiles exceed the Debye length, majority carriers no longer behave according to the distribution of the dopants. Instead, a measure of the profile of the doping gradients provides an “effective” profile that better matches the profile of the majority carrier density.