Debye-Hückel equation
Encyclopedia
The Debye–Hückel equation and Debye–Hückel limiting law, were derived by Peter Debye
and Erich Hückel
, who developed a theory with which to calculate activity coefficient
s of electrolyte
solutions. Activities
, rather than concentrations, are needed in many chemical calculations because solutions that contain ionic solutes do not behave ideally even at very low concentrations. The activity is proportional to the concentration by a factor known as the activity coefficient
, and takes into account the interaction energy
of ions in the solution.
In order to calculate the activity
of an ion
in a solution, one must know the concentration
and the activity coefficient,
. The activity of some ion species C, 
, is equal to a dimensionless measure of the concentration of C, 
multiplied by the activity coefficient of C, 
.
The Debye-Hückel limiting law enables one to determine the activity coefficient of an ion in a dilute solution of known ionic strength
. The equation is
It is important to note that because the ions in the solution act together, the activity coefficient obtained from this equation is actually a mean activity coefficient.
.
In the same year they first published this paper, Debye and Hückel, hereinafter D&H, also released a paper that covered their initial characterization of solutions under the influence of electric fields called "On the Theory of Electrolytes. II. Limiting Law for Electric Conductivity," but that subsequent paper is not (yet) covered here.
In the following summary (as yet incomplete and unchecked), modern notation and terminology are used, from both chemistry and mathematics, in order to prevent confusion. Also, with a few exceptions to improve clarity, the subsections in this summary are (very) condensed versions of the same subsections of the original paper.
in classical form is
D&H say that, due to the "mutual electrostatic forces between the ions," it is necessary to modify the Guldberg-Waage equation by replacing
with 
, where 
is an overall activity coefficient, not a "special" activity coefficient
(a separate activity coefficient associated for each species)—which is what is used in modern chemistry .
The relationship between
and the special activity coefficients, 
is
,
and 
, to express the effect of electrostatic forces in an electrolyte on its thermodynamic state. Specifically, they split most of the thermodynamic potentials into classical and electrostatic terms.
D&H give the total differential of
as
By the definition of the total differential, this means that
which are useful further on.
As stated previously, the internal energy is divided into two parts,
Similarly, the Helmholtz free entropy is also divided into two parts,
D&H state, without giving the logic, that
It would seem that, without some justification,
.
Without mentioning it specifically, D&H later give what might be the required (above) justification while arguing that
, an assumption that the solvent is incompressible.
The definition of the Gibbs free entropy
,
, is
.
D&H give the total differential of
as
.
At this point D&H note that, for water containing 1 mole per liter of potassium chloride
(nominal pressure and temperature aren't given), the electric pressure,
, amounts to 20 atmospheres. Furthermore, they note that this level of pressure gives a relative volume change of 0.001. Therefore, they neglect change in volume of water due to electric pressure, writing
and put
.
D&H say that, according to Planck, the classical part of the Gibbs free entropy is
.
Species zero is the solvent. The definition of
is as follows, where lower case letters indicate the particle specific versions of the corresponding extensive properties:
.
D&H don't say so, but the functional form for
may be derived from the functional dependence of the chemical potential of a component of an ideal mixture upon its mole fraction.
D&H note that the internal energy,
, of a solution is lowered by the electrical interaction of its ions, but that this effect can't be determined by using the crystallographic approximation for distances between dissimilar atoms (the cube root of the ratio of total volume to the number of particles in the volume). This is because there is more thermal motion in a liquid solution than in a crystal. The thermal motion tends to smear out the natural lattice that would otherwise be constructed by the ions. Instead, D&H introduce the concept of an ionic cloud. Like the crystal lattice, each ion still attempts to surround itself with oppositely charged ions, but in a more free-form manner; at small distances away from positive ions, one is more likely to find negative ions and vice versa.
.
To bring an ion of species i, initially far away, to a point
within the ion cloud requires interaction energy
in the amount of
, where 
is the elementary charge
and
is the value of the scalar electric potential
field at
. If electric forces were the only factor in play, the minimum energy configuration of all the ions would be achieved in a close-packed lattice configuration. However, the ions are in thermal equilibrium
with each other and they are relatively free to move. Thus they obey Boltzmann statistics and form a Boltzmann distribution
. All species' number densities
,
, are altered from their bulk (overall average) values, 
, by the corresponding Boltzmann factor
,
, where 
is the Boltzmann constant and 
is the temperature (http://www.pma.caltech.edu/Courses/ph136/yr2006/text.html, section 19.3). Thus,
at every point in the cloud. Note that in the infinite temperature limit, all ions are distributed uniformly, with no regard for their electrostatic interactions.
The charge density
is related to the number density:
.
When combining this result for the charge density with the Poisson equation from electrostatics, a form of the Poisson-Boltzmann equation
results:
.
This equation is difficult to solve and does not follow the principle of linear superposition for the relationship between the number of charges and the strength of the potential field. However, for sufficiently low concentrations of ions, a first order Taylor series approximation for the exponential function may be used (
for 
) to create a linear differential equation (Hamann, Hamnett, and Vielstich. Electrochemistry. Wiley-VCH. section 2.4.2). D&H say that this approximation holds at large distances between ions, which is the same as saying that the concentration is low. Lastly, they claim without proof that the addition of more terms in the expansion has little effect on the final solution. Thus,
.
The Poisson-Boltzmann equation is transformed to
,
because the first summation is zero due to electroneutrality.
Factor out the scalar potential and assign the leftovers, which are constant, to
. Also, let 
be the ionic strength
of the solution:
,
.
So, the fundamental equation is reduced to a form of the Helmholtz equation
:(http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf section 3.1)
.
Today,
is called the Debye screening length
. D&H recognize the importance of the parameter in their paper and characterize it as a measure of the thickness of the ion atmosphere, which is an electrical double layer of the Guoy-Chapman type.
The equation may be expressed in spherical coordinates by taking
at some arbitrary ion (http://hyperphysics.phy-astr.gsu.edu/hbase/electric/laplace.html):
.
The equation has the following general solution; keep in mind that
is a positive constant:
.
The electric potential is zero at infinity by definition, so
must be zero.
In the next step, D&H assume that there is a certain radius,
, beyond which no ions in the atmosphere may approach the (charge) center of the singled out ion. This radius may be due to the physical size of the ion itself, the sizes of the ions in the cloud, and any water molecules that surround the ions. Mathematically, they treat the singled out ion as a point charge to which one may not approach within the radius 
.
The potential of a point charge by itself is:
.
D&H say that the total potential inside the sphere is
,
where
is a constant that represents the potential added by the ionic atmosphere. No justification for 
being a constant is given. However, one can see that this is the case by considering that any spherical static charge distribution is subject to the mathematics of the shell theorem
. The shell theorem says that no force is exerted on charged particles inside a sphere (of arbitrary charge) (http://hyperphysics.phy-astr.gsu.edu/hbase/electric/potsph.html). Since the ion atmosphere is assumed to be (time-averaged) spherically symmetric, with charge varying as a function of radius
, it may be represented as an infinite series of concentric charge shells. Therefore, inside the radius 
, the ion atmosphere exerts no force. If the force is zero, then the potential is a constant (by definition).
In a combination of the continuously distributed model which gave the Poisson-Boltzmann equation and the model of the point charge, it is assumed that at the radius
, there is a continuity of 
and its first derivative. Thus,
,
,
, and
.
By the definition of electric potential energy
, the potential energy associated with the singled out ion in the ion atmosphere is
Notice that this only requires knowledge of the charge of the singled out ion and the potential of all the other ions.
To calculate the potential energy of the entire electrolyte solution, one must use the multiple charge generalization for electric potential energy.
The differential equation is ready for solution (as stated above, the equation only holds for low concentrations):
Using the Buckingham π theorem on this problem results in the following dimensionless groups:
is called the reduced scalar electric potential field. 
is called the reduced radius. The existing groups may be recombined to form two other dimensionless groups for substitution into the differential equation. The first is what could be called the square of the reduced inverse screening length, 
. The second could be called the reduced central ion charge, 
(with a capital Z). Note that, though 
is already dimensionless, without the substitution given below, the differential equation would still be dimensional.
To obtain the nondimensionalized differential equation and initial conditions, use the
groups to eliminate 
in favor of 
, then eliminate 
in favor of 
while carrying out the chain rule and substituting 
, then eliminate 
in favor of 
(no chain rule needed), then eliminate 
in favor of 
, then eliminate 
in favor of 
. The resulting equations are as follows:
For table salt in 0.01 M solution at 25°C, a typical value of
is 0.0005636, while a typical value of 
is 7.017, highlighting the fact that, in low concentrations, 
is a target for a zero order of magnitude approximation such as perturbation analysis. Unfortunately, because of the boundary condition at infinity, regular perturbation does not work. The same boundary condition prevents us from finding the exact solution to the equations. Singular perturbation may work, however.
Typical examples are: measurements of vapour pressure, freezing point, osmotic pressure (indirect methods) and measurement of electric potential in cells (direct method).
Going towards high dilutions goods results have been found using liquid membrane cells, it has been possible to investigate aqueous media 10−4 M and it has been found that for 1:1 electrolytes (as NaCl or KCl) the Debye–Hückel equation is totally correct, but for 2:2 or 3:2 electrolytes it is possible to find negative deviation from the Debye–Hückel limit law: this strange behavior can be observed only in the very dilute area, and in more concentrate regions the deviation becomes positive.
It is possible that Debye–Hückel equation is not able to foresee this behavior because of the linearization of the Poisson-Boltzmann equation, or maybe not: studies about this have been started only during the last years of the 20th century because before it wasn’t possible to investigate the 10−4 M region, so it is possible that during the next years new theories will be born.
A number of approaches have been proposed to extend the validity of the law to concentration ranges as commonly encountered in chemistry
One such Extended Debye-Hückel Equation is given by:
where
as its common logarithm
is the activity coefficient,
is the integer charge of the ion (1 for H+, 2 for Mg2+ etc.), 
is the ionic strength of the aqueous solution, and 
is the size or effective diameter of the ion in angstrom
. The effective hydrated radius of the ion, a is the radius of the ion and its closely bound water molecules. Large ions and less highly charged ions bind water less tightly and have smaller hydrated radii than smaller, more highly charged ions. Typical values are 3Å for ions such as H+,Cl-,CN-, and HCOO-. The effective diameter for the hydronium ion is 9Å.
and 
are constants with values of respectively 0.5085 and 0.3281 at 25°C in water .
The Extended Debye-Hückel Equation provides accurate results for μ ≤ 0.1 M. For solutions of greater ionic strengths, the Pitzer equations
should be used. In these solutions the activity coefficient may actually increase with ionic strength.
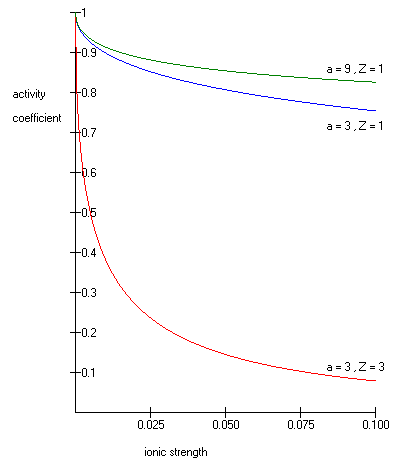The Debye-Hückel Equation cannot be used in the solutions of surfactant
s where the presence of micelle
s influences on the electrochemical properties of the system (even rough judgement overestimates γ for ~50%).
Peter Debye
Peter Joseph William Debye FRS was a Dutch physicist and physical chemist, and Nobel laureate in Chemistry.-Early life:...
and Erich Hückel
Erich Hückel
Erich Armand Arthur Joseph Hückel was a German physicist and physical chemist. He is known for two major contributions:*The Debye–Hückel theory of electrolytic solutions...
, who developed a theory with which to calculate activity coefficient
Activity coefficient
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
s of electrolyte
Electrolyte
In chemistry, an electrolyte is any substance containing free ions that make the substance electrically conductive. The most typical electrolyte is an ionic solution, but molten electrolytes and solid electrolytes are also possible....
solutions. Activities
Activity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
, rather than concentrations, are needed in many chemical calculations because solutions that contain ionic solutes do not behave ideally even at very low concentrations. The activity is proportional to the concentration by a factor known as the activity coefficient
, and takes into account the interaction energyInteraction energy
In physics, interaction energy is the contribution to the total energy that is caused by an interaction between the objects being considered.The interaction energy usually depends on the relative position of the objects...
of ions in the solution.
Debye-Hückel limiting law
- For the principles used to derive this equation see Debye-Hückel theory
In order to calculate the activity
Activity (chemistry)
In chemical thermodynamics, activity is a measure of the “effective concentration” of a species in a mixture, meaning that the species' chemical potential depends on the activity of a real solution in the same way that it would depend on concentration for an ideal solution.By convention, activity...
of an ion
Ion
An ion is an atom or molecule in which the total number of electrons is not equal to the total number of protons, giving it a net positive or negative electrical charge. The name was given by physicist Michael Faraday for the substances that allow a current to pass between electrodes in a...
in a solution, one must know the concentration
Concentration
In chemistry, concentration is defined as the abundance of a constituent divided by the total volume of a mixture. Four types can be distinguished: mass concentration, molar concentration, number concentration, and volume concentration...
and the activity coefficient,
. The activity of some ion species C, , is equal to a dimensionless measure of the concentration of C, multiplied by the activity coefficient of C, .
-
represents the concentration of the chosen standard state, e.g. 1 mol/kg if we work in molality.
The Debye-Hückel limiting law enables one to determine the activity coefficient of an ion in a dilute solution of known ionic strength
Ionic strength
The ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
. The equation is
-
is the charge number of ion species i
is the elementary chargeElementary chargeThe elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
is the inverse of the Debye screening lengthDebye lengthIn plasma physics, the Debye length , named after the Dutch physicist and physical chemist Peter Debye, is the scale over which mobile charge carriers screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge...
, defined below
is the relative permittivity of the solvent
is the permittivity of free space
is Boltzmann's constant
is the temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
of the solution
is Avogadro's numberAvogadro's numberIn chemistry and physics, the Avogadro constant is defined as the ratio of the number of constituent particles N in a sample to the amount of substance n through the relationship NA = N/n. Thus, it is the proportionality factor that relates the molar mass of an entity, i.e...
is the ionic strengthIonic strengthThe ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
of the solution, defined below
is a constant that depends on the solvent. If I is expressed in terms of molality, instead of molarity (as in the equation above and in the rest of this article), then an experimental value for A is 1.172 
. In fact it is common to use a base-10 logarithm, in which case we factor 
, so A is 0.509 
.
It is important to note that because the ions in the solution act together, the activity coefficient obtained from this equation is actually a mean activity coefficient.
Summary of Debye & Hückel's first paper on the theory of dilute electrolytes
The English title of the paper is called "On the Theory of Electrolytes. I. Freezing Point Depression and Related Phenomena." It was originally published in volume 24 of a German-language journal, called Physikalische Zeitschrift, in 1923. An English translationof the paper is included in a book of collected papers presented to Debye by "his pupils, friends, and the publishers on the occasion of his seventieth birthday on March 24, 1954." The paper deals with the calculation of properties of electrolyte solutions that are not under the influence of net electric fields, thus it deals with electrostaticsElectrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
.
In the same year they first published this paper, Debye and Hückel, hereinafter D&H, also released a paper that covered their initial characterization of solutions under the influence of electric fields called "On the Theory of Electrolytes. II. Limiting Law for Electric Conductivity," but that subsequent paper is not (yet) covered here.
In the following summary (as yet incomplete and unchecked), modern notation and terminology are used, from both chemistry and mathematics, in order to prevent confusion. Also, with a few exceptions to improve clarity, the subsections in this summary are (very) condensed versions of the same subsections of the original paper.
Introduction
D&H note that the Guldberg-Waage formula for electrolyte species in chemical reaction equilibriumChemical equilibrium
In a chemical reaction, chemical equilibrium is the state in which the concentrations of the reactants and products have not yet changed with time. It occurs only in reversible reactions, and not in irreversible reactions. Usually, this state results when the forward reaction proceeds at the same...
in classical form is
-
is a notation for multiplication
is a dummy variableFree variables and bound variablesIn mathematics, and in other disciplines involving formal languages, including mathematical logic and computer science, a free variable is a notation that specifies places in an expression where substitution may take place...
indicating the species
is the number of species participating in the reaction
is the mole fraction of species 
is the stoichiometric coefficient of species 
- K is the equilibrium constant.
D&H say that, due to the "mutual electrostatic forces between the ions," it is necessary to modify the Guldberg-Waage equation by replacing
with , where is an overall activity coefficient, not a "special" activity coefficientActivity coefficient
An activity coefficient is a factor used in thermodynamics to account for deviations from ideal behaviour in a mixture of chemical substances. In an ideal mixture, the interactions between each pair of chemical species are the same and, as a result, properties of the mixtures can be expressed...
(a separate activity coefficient associated for each species)—which is what is used in modern chemistry .
The relationship between
and the special activity coefficients, isFundamentals
D&H use the Helmholtz and Gibbs free entropiesFree entropy
A thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy. Also known as a Massieu, Planck, or Massieu-Planck potentials , or free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function...
,
and , to express the effect of electrostatic forces in an electrolyte on its thermodynamic state. Specifically, they split most of the thermodynamic potentials into classical and electrostatic terms.-
is Helmholtz free entropyFree entropyA thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy. Also known as a Massieu, Planck, or Massieu-Planck potentials , or free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function...
is entropyEntropyEntropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when...
is internal energyInternal energyIn thermodynamics, the internal energy is the total energy contained by a thermodynamic system. It is the energy needed to create the system, but excludes the energy to displace the system's surroundings, any energy associated with a move as a whole, or due to external force fields. Internal...
is temperatureTemperatureTemperature is a physical property of matter that quantitatively expresses the common notions of hot and cold. Objects of low temperature are cold, while various degrees of higher temperatures are referred to as warm or hot...
is Helmholtz free energyHelmholtz free energyIn thermodynamics, the Helmholtz free energy is a thermodynamic potential that measures the “useful” work obtainable from a closed thermodynamic system at a constant temperature and volume...
D&H give the total differential of
as-
is pressurePressurePressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
is volumeVolumeVolume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
By the definition of the total differential, this means that
-
and
-
,
which are useful further on.
As stated previously, the internal energy is divided into two parts,
-
indicates the classical part
indicates the electric part
Similarly, the Helmholtz free entropy is also divided into two parts,
D&H state, without giving the logic, that
It would seem that, without some justification,
.Without mentioning it specifically, D&H later give what might be the required (above) justification while arguing that
, an assumption that the solvent is incompressible.The definition of the Gibbs free entropy
Free entropy
A thermodynamic free entropy is an entropic thermodynamic potential analogous to the free energy. Also known as a Massieu, Planck, or Massieu-Planck potentials , or free information. In statistical mechanics, free entropies frequently appear as the logarithm of a partition function...
,
, is.-
is Gibbs free energyGibbs free energyIn thermodynamics, the Gibbs free energy is a thermodynamic potential that measures the "useful" or process-initiating work obtainable from a thermodynamic system at a constant temperature and pressure...
D&H give the total differential of
as.At this point D&H note that, for water containing 1 mole per liter of potassium chloride
Potassium chloride
The chemical compound potassium chloride is a metal halide salt composed of potassium and chlorine. In its pure state, it is odorless and has a white or colorless vitreous crystal appearance, with a crystal structure that cleaves easily in three directions. Potassium chloride crystals are...
(nominal pressure and temperature aren't given), the electric pressure,
, amounts to 20 atmospheres. Furthermore, they note that this level of pressure gives a relative volume change of 0.001. Therefore, they neglect change in volume of water due to electric pressure, writingand put
.D&H say that, according to Planck, the classical part of the Gibbs free entropy is
.
-
is a species
is the number of different particle types in solution
is the number of particles of species i
is the particle specific Gibbs free entropy of species i
is Boltzmann's constant
is the mole fraction of species i
Species zero is the solvent. The definition of
is as follows, where lower case letters indicate the particle specific versions of the corresponding extensive properties:.D&H don't say so, but the functional form for
may be derived from the functional dependence of the chemical potential of a component of an ideal mixture upon its mole fraction.D&H note that the internal energy,
, of a solution is lowered by the electrical interaction of its ions, but that this effect can't be determined by using the crystallographic approximation for distances between dissimilar atoms (the cube root of the ratio of total volume to the number of particles in the volume). This is because there is more thermal motion in a liquid solution than in a crystal. The thermal motion tends to smear out the natural lattice that would otherwise be constructed by the ions. Instead, D&H introduce the concept of an ionic cloud. Like the crystal lattice, each ion still attempts to surround itself with oppositely charged ions, but in a more free-form manner; at small distances away from positive ions, one is more likely to find negative ions and vice versa.The Potential Energy of an Arbitrary Ion Solution
Electroneutrality of a solution requires that.
-
is the total number of ions of species i in the solution
is the charge number of species i.
To bring an ion of species i, initially far away, to a point
within the ion cloud requires interaction energyInteraction energy
In physics, interaction energy is the contribution to the total energy that is caused by an interaction between the objects being considered.The interaction energy usually depends on the relative position of the objects...
in the amount of
, where is the elementary chargeElementary charge
The elementary charge, usually denoted as e, is the electric charge carried by a single proton, or equivalently, the absolute value of the electric charge carried by a single electron. This elementary charge is a fundamental physical constant. To avoid confusion over its sign, e is sometimes called...
and
is the value of the scalar electric potentialElectric potential
In classical electromagnetism, the electric potential at a point within a defined space is equal to the electric potential energy at that location divided by the charge there...
field at
. If electric forces were the only factor in play, the minimum energy configuration of all the ions would be achieved in a close-packed lattice configuration. However, the ions are in thermal equilibriumThermal equilibrium
Thermal equilibrium is a theoretical physical concept, used especially in theoretical texts, that means that all temperatures of interest are unchanging in time and uniform in space...
with each other and they are relatively free to move. Thus they obey Boltzmann statistics and form a Boltzmann distribution
Boltzmann distribution
In chemistry, physics, and mathematics, the Boltzmann distribution is a certain distribution function or probability measure for the distribution of the states of a system. It underpins the concept of the canonical ensemble, providing its underlying distribution...
. All species' number densities
Number density
In physics, astronomy, and chemistry, number density is an intensive quantity used to describe the degree of concentration of countable objects in the three-dimensional physical space...
,
, are altered from their bulk (overall average) values, , by the corresponding Boltzmann factorBoltzmann factor
In physics, the Boltzmann factor is a weighting factor that determines the relative probability of a particle to be in a state i in a multi-state system in thermodynamic equilibrium at temperature T...
,
, where is the Boltzmann constant and is the temperature (http://www.pma.caltech.edu/Courses/ph136/yr2006/text.html, section 19.3). Thus,
-
- V is the volume of the solution
at every point in the cloud. Note that in the infinite temperature limit, all ions are distributed uniformly, with no regard for their electrostatic interactions.
The charge density
Charge density
The linear, surface, or volume charge density is the amount of electric charge in a line, surface, or volume, respectively. It is measured in coulombs per meter , square meter , or cubic meter , respectively, and represented by the lowercase Greek letter Rho . Since there are positive as well as...
is related to the number density:
.When combining this result for the charge density with the Poisson equation from electrostatics, a form of the Poisson-Boltzmann equation
Poisson-Boltzmann equation
The Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913...
results:
.This equation is difficult to solve and does not follow the principle of linear superposition for the relationship between the number of charges and the strength of the potential field. However, for sufficiently low concentrations of ions, a first order Taylor series approximation for the exponential function may be used (
for ) to create a linear differential equation (Hamann, Hamnett, and Vielstich. Electrochemistry. Wiley-VCH. section 2.4.2). D&H say that this approximation holds at large distances between ions, which is the same as saying that the concentration is low. Lastly, they claim without proof that the addition of more terms in the expansion has little effect on the final solution. Thus,.The Poisson-Boltzmann equation is transformed to
,because the first summation is zero due to electroneutrality.
Factor out the scalar potential and assign the leftovers, which are constant, to
. Also, let be the ionic strengthIonic strength
The ionic strength of a solution is a measure of the concentration of ions in that solution. Ionic compounds, when dissolved in water, dissociate into ions. The total electrolyte concentration in solution will affect important properties such as the dissociation or the solubility of different salts...
of the solution:
,.So, the fundamental equation is reduced to a form of the Helmholtz equation
Helmholtz equation
The Helmholtz equation, named for Hermann von Helmholtz, is the elliptic partial differential equation\nabla^2 A + k^2 A = 0where ∇2 is the Laplacian, k is the wavenumber, and A is the amplitude.-Motivation and uses:...
:(http://guava.physics.uiuc.edu/~nigel/courses/569/Essays_2004/files/lu.pdf section 3.1)
.Today,
is called the Debye screening lengthDebye length
In plasma physics, the Debye length , named after the Dutch physicist and physical chemist Peter Debye, is the scale over which mobile charge carriers screen out electric fields in plasmas and other conductors. In other words, the Debye length is the distance over which significant charge...
. D&H recognize the importance of the parameter in their paper and characterize it as a measure of the thickness of the ion atmosphere, which is an electrical double layer of the Guoy-Chapman type.
The equation may be expressed in spherical coordinates by taking
at some arbitrary ion (http://hyperphysics.phy-astr.gsu.edu/hbase/electric/laplace.html):.The equation has the following general solution; keep in mind that
is a positive constant:.
-
, 
, and 
are undetermined constants
The electric potential is zero at infinity by definition, so
must be zero.In the next step, D&H assume that there is a certain radius,
, beyond which no ions in the atmosphere may approach the (charge) center of the singled out ion. This radius may be due to the physical size of the ion itself, the sizes of the ions in the cloud, and any water molecules that surround the ions. Mathematically, they treat the singled out ion as a point charge to which one may not approach within the radius .The potential of a point charge by itself is:
.D&H say that the total potential inside the sphere is
,where
is a constant that represents the potential added by the ionic atmosphere. No justification for being a constant is given. However, one can see that this is the case by considering that any spherical static charge distribution is subject to the mathematics of the shell theoremShell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
. The shell theorem says that no force is exerted on charged particles inside a sphere (of arbitrary charge) (http://hyperphysics.phy-astr.gsu.edu/hbase/electric/potsph.html). Since the ion atmosphere is assumed to be (time-averaged) spherically symmetric, with charge varying as a function of radius
, it may be represented as an infinite series of concentric charge shells. Therefore, inside the radius , the ion atmosphere exerts no force. If the force is zero, then the potential is a constant (by definition).In a combination of the continuously distributed model which gave the Poisson-Boltzmann equation and the model of the point charge, it is assumed that at the radius
, there is a continuity of and its first derivative. Thus,,,, and.By the definition of electric potential energy
Electric potential energy
Electric potential energy, or electrostatic potential energy, is a potential energy that results from conservative Coulomb forces and is associated with the configuration of a particular set of point charges within a defined system...
, the potential energy associated with the singled out ion in the ion atmosphere is
Notice that this only requires knowledge of the charge of the singled out ion and the potential of all the other ions.
To calculate the potential energy of the entire electrolyte solution, one must use the multiple charge generalization for electric potential energy.
Nondimensionalization
This section was created without reference to the original paper and there are some errors in it (for instance, the ionic strength is off by a factor of two). Once these are rectified, this section should probably be moved to the nondimensionalization article and then be linked from here, since the nondimensional version of the Poisson-Boltzmann equation isn't necessary to understand the D&H theory.The differential equation is ready for solution (as stated above, the equation only holds for low concentrations):
Using the Buckingham π theorem on this problem results in the following dimensionless groups:
is called the reduced scalar electric potential field. is called the reduced radius. The existing groups may be recombined to form two other dimensionless groups for substitution into the differential equation. The first is what could be called the square of the reduced inverse screening length, . The second could be called the reduced central ion charge, (with a capital Z). Note that, though is already dimensionless, without the substitution given below, the differential equation would still be dimensional.To obtain the nondimensionalized differential equation and initial conditions, use the
groups to eliminate in favor of , then eliminate in favor of while carrying out the chain rule and substituting , then eliminate in favor of (no chain rule needed), then eliminate in favor of , then eliminate in favor of . The resulting equations are as follows:For table salt in 0.01 M solution at 25°C, a typical value of
is 0.0005636, while a typical value of is 7.017, highlighting the fact that, in low concentrations, is a target for a zero order of magnitude approximation such as perturbation analysis. Unfortunately, because of the boundary condition at infinity, regular perturbation does not work. The same boundary condition prevents us from finding the exact solution to the equations. Singular perturbation may work, however.Experimental verification of the theory
To verify the validity of the Debye-Hückel theory, many experimental ways have been tried, measuring the activity coefficients: the problem is that we need to go towards very high dilutions.Typical examples are: measurements of vapour pressure, freezing point, osmotic pressure (indirect methods) and measurement of electric potential in cells (direct method).
Going towards high dilutions goods results have been found using liquid membrane cells, it has been possible to investigate aqueous media 10−4 M and it has been found that for 1:1 electrolytes (as NaCl or KCl) the Debye–Hückel equation is totally correct, but for 2:2 or 3:2 electrolytes it is possible to find negative deviation from the Debye–Hückel limit law: this strange behavior can be observed only in the very dilute area, and in more concentrate regions the deviation becomes positive.
It is possible that Debye–Hückel equation is not able to foresee this behavior because of the linearization of the Poisson-Boltzmann equation, or maybe not: studies about this have been started only during the last years of the 20th century because before it wasn’t possible to investigate the 10−4 M region, so it is possible that during the next years new theories will be born.
Extensions of the theory
Warning: The notation in this section is (currently) different than in the rest of the article.A number of approaches have been proposed to extend the validity of the law to concentration ranges as commonly encountered in chemistry
One such Extended Debye-Hückel Equation is given by:
where
as its common logarithmCommon logarithm
The common logarithm is the logarithm with base 10. It is also known as the decadic logarithm, named after its base. It is indicated by log10, or sometimes Log with a capital L...
is the activity coefficient,
is the integer charge of the ion (1 for H+, 2 for Mg2+ etc.), is the ionic strength of the aqueous solution, and is the size or effective diameter of the ion in angstromÅngström
The angstrom or ångström, is a unit of length equal to 1/10,000,000,000 of a meter . Its symbol is the Swedish letter Å....
. The effective hydrated radius of the ion, a is the radius of the ion and its closely bound water molecules. Large ions and less highly charged ions bind water less tightly and have smaller hydrated radii than smaller, more highly charged ions. Typical values are 3Å for ions such as H+,Cl-,CN-, and HCOO-. The effective diameter for the hydronium ion is 9Å.
and are constants with values of respectively 0.5085 and 0.3281 at 25°C in water .The Extended Debye-Hückel Equation provides accurate results for μ ≤ 0.1 M. For solutions of greater ionic strengths, the Pitzer equations
Pitzer equations
Pitzer equations are important for the understanding of the behaviour of ions dissolved in natural waters such as rivers, lakes and sea-water. The parameters of the Pitzer equations are linear combinations of parameters, of a virial expansion of the excess Gibbs free energy, which characterise...
should be used. In these solutions the activity coefficient may actually increase with ionic strength.
Surfactant
Surfactants are compounds that lower the surface tension of a liquid, the interfacial tension between two liquids, or that between a liquid and a solid...
s where the presence of micelle
Micelle
A micelle is an aggregate of surfactant molecules dispersed in a liquid colloid. A typical micelle in aqueous solution forms an aggregate with the hydrophilic "head" regions in contact with surrounding solvent, sequestering the hydrophobic single tail regions in the micelle centre. This phase is...
s influences on the electrochemical properties of the system (even rough judgement overestimates γ for ~50%).
See also
- Strong electrolyteStrong electrolyteA strong electrolyte is a solute that completely, or almost completely, ionizes or dissociates in a solution. These ions are good conductors of electric current in the solution....
- Weak electrolyte
- Ionic atmosphereIonic atmosphereIonic Atmosphere is a concept employed in Debye-Hückel theory which explains the conductivity behaviour of electrolytic solutions. It can be generally defined as the area at which a charged entity is capable of attracting an entity of the opposite charge....
- Debye–Hückel theoryDebye–Hückel theoryThe Debye–Hückel theory was proposed by Peter Debye and Erich Hückel as a theoretical explanation for departures from ideality in solutions of electrolytes. It was based on an extremely simplified model of the electrolyte solution but nevertheless gave accurate predictions of mean activity...
External links
- For easy calculation of activity coefficients in (non-micellar) solutions, check out the IUPAC open project Aq-solutions (freeware).
- Gold BookGold BookThe Compendium of Chemical Terminology is a book published by the International Union of Pure and Applied Chemistry containing internationally accepted definitions for terms in chemistry...
definition