
Difference hierarchy
Encyclopedia
In set theory
, the difference hierarchy over a pointclass
is a hierarchy
of larger pointclasses
generated by taking difference
s of sets. If Γ is a pointclass, then the set of differences in Γ is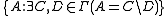 . In usual notation, this set is denoted by 2-Γ. The next level of the hierarchy is denoted by 3-Γ and consists of differences of three sets:
. In usual notation, this set is denoted by 2-Γ. The next level of the hierarchy is denoted by 3-Γ and consists of differences of three sets:
 . This definition can be extended recursively into the transfinite to α-Γ for some ordinal
. This definition can be extended recursively into the transfinite to α-Γ for some ordinal
α.
In the Borel and projective hierarchies, Felix Hausdorff
proved that the countable levels of the
difference hierarchy over Π0γ and Π1γ give
Δ0γ+1 and Δ1γ+1, respectively.
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, the difference hierarchy over a pointclass
Pointclass
In the mathematical field of descriptive set theory, a pointclass is a collection of sets of points, where a point is ordinarily understood to be an element of some perfect Polish space. In practice, a pointclass is usually characterized by some sort of definability property; for example, the...
is a hierarchy
Hierarchy (mathematics)
In mathematics, a hierarchy is a preorder, i.e. an ordered set. The term is used to stress a natural hierarchical relation among the elements. In particular, it is the preferred terminology for posets whose elements are classes of objects of increasing complexity. In that case, the preorder...
of larger pointclasses
generated by taking difference
Complement (set theory)
In set theory, a complement of a set A refers to things not in , A. The relative complement of A with respect to a set B, is the set of elements in B but not in A...
s of sets. If Γ is a pointclass, then the set of differences in Γ is
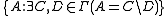 . In usual notation, this set is denoted by 2-Γ. The next level of the hierarchy is denoted by 3-Γ and consists of differences of three sets:
. In usual notation, this set is denoted by 2-Γ. The next level of the hierarchy is denoted by 3-Γ and consists of differences of three sets: . This definition can be extended recursively into the transfinite to α-Γ for some ordinal
. This definition can be extended recursively into the transfinite to α-Γ for some ordinalOrdinal number
In set theory, an ordinal number, or just ordinal, is the order type of a well-ordered set. They are usually identified with hereditarily transitive sets. Ordinals are an extension of the natural numbers different from integers and from cardinals...
α.
In the Borel and projective hierarchies, Felix Hausdorff
Felix Hausdorff
Felix Hausdorff was a Jewish German mathematician who is considered to be one of the founders of modern topology and who contributed significantly to set theory, descriptive set theory, measure theory, function theory, and functional analysis.-Life:Hausdorff studied at the University of Leipzig,...
proved that the countable levels of the
difference hierarchy over Π0γ and Π1γ give
Δ0γ+1 and Δ1γ+1, respectively.

