Domain coloring
Encyclopedia
Douglas N. Arnold
Douglas Norman Arnold is a mathematician whose research focuses on the numerical analysis of partial differential equations with applications in mechanics and other fields in physics. , he is McKnight Presidential Professor of Mathematics at the University of Minnesota.Arnold studied mathematics as...
that he dates to 1997 http://www.ima.umn.edu/~arnold/complex.html.
Insufficient dimensions
A real function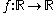
(for example 
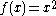)can be graphed
Graph of a function
In mathematics, the graph of a function f is the collection of all ordered pairs . In particular, if x is a real number, graph means the graphical representation of this collection, in the form of a curve on a Cartesian plane, together with Cartesian axes, etc. Graphing on a Cartesian plane is...
using two Cartesian coordinates on a plane
Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
.
A graph of a complex function
of onecomplex variable lives in a space with two complex dimensions. Since the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
itself is two dimensional, a graph of a complex function is an object in four real dimensions. That makes complex functions difficult to visualize in our three dimensional space. One way of depicting
holomorphic functions is with a Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
.
Visual encoding of complex numbers
Given a complex number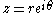
, the phase (also known as argument)
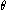can be represented by a hue, and the modulus 
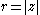isrepresented by either intensity or variations in intensity. The arrangement
of hues is arbitrary, but often it follows the color wheel
Color wheel
A color wheel or color circle is an abstract illustrative organization of color hues around a circle that shows relationships between primary colors, secondary colors, complementary colors, etc....
. Sometimes the phase is represented by a specific gradient rather than hue.
Example
The following image depicts the sineSine
In mathematics, the sine function is a function of an angle. In a right triangle, sine gives the ratio of the length of the side opposite to an angle to the length of the hypotenuse.Sine is usually listed first amongst the trigonometric functions....
function
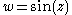from 
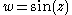to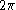 
on the real axis and
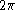to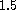 
on the imaginary axis.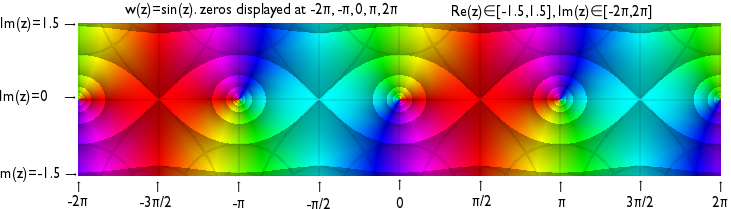
See also
- Conformal picturesConformal picturesHere are examples of conformal maps understood as deforming pictures. This technique is a generalization of domain coloring where the domain space is not colored by a fixed infinite color wheel but by a finite picture tiling the plane...
where the domain is colored with a picture and not with a fixed color wheelColor wheelA color wheel or color circle is an abstract illustrative organization of color hues around a circle that shows relationships between primary colors, secondary colors, complementary colors, etc....
.
External links
- Color Graphs of Complex Functions
- Visualizing complex-valued functions in the plane.
- Gallery of Complex Functions
- Complex Mapper by Alessandro Rosa
- John Davis software - S-Lang script for Domain Coloring
- Open source C and Python domain coloring software
- Enhanced 3D Domain coloring
- Java domain coloring software (In development)