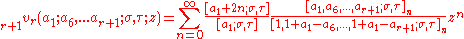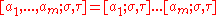Elliptic hypergeometric series
Encyclopedia
In mathematics, an elliptic hypergeometric series is a series Σcn such that the ratio
cn/cn−1 is an elliptic function
of n, analogous to generalized hypergeometric series where the ratio is a rational function
of n, and basic hypergeometric series
where the ratio is a periodic function of the complex number n. They were introduced by in their study of elliptic 6-j symbols.
For surveys of elliptic hypergeometric series see or .
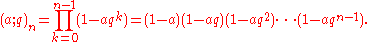
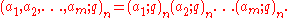
The modified Jacobi theta function with argument x and nome p is defined by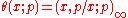

The elliptic shifted factorial is defined by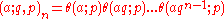
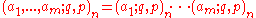
The theta hypergeometric series r+1Er is defined by
The very-well-poised theta hypergeometric series r+1Vr is defined by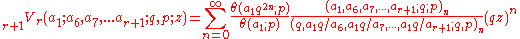
The bilateral theta hypergeometric series rGr is defined by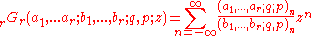
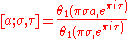
where the Jacobi theta function is defined by
The additive elliptic shifted factorials are defined by
The additive theta hypergeometric series r+1er is defined by
The additive very-well-poised theta hypergeometric series r+1vr is defined by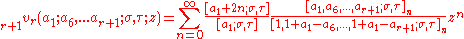
cn/cn−1 is an elliptic function
Elliptic function
In complex analysis, an elliptic function is a function defined on the complex plane that is periodic in two directions and at the same time is meromorphic...
of n, analogous to generalized hypergeometric series where the ratio is a rational function
Rational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
of n, and basic hypergeometric series
Basic hypergeometric series
In mathematics, Heine's basic hypergeometric series, or hypergeometric q-series, are q-analog generalizations of generalized hypergeometric series, and are in turn generalized by elliptic hypergeometric series....
where the ratio is a periodic function of the complex number n. They were introduced by in their study of elliptic 6-j symbols.
For surveys of elliptic hypergeometric series see or .
Definitions
The q-Pochhammer symbol is defined by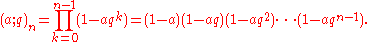
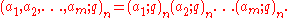
The modified Jacobi theta function with argument x and nome p is defined by
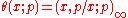

The elliptic shifted factorial is defined by
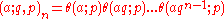
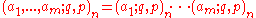
The theta hypergeometric series r+1Er is defined by

The very-well-poised theta hypergeometric series r+1Vr is defined by
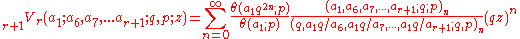
The bilateral theta hypergeometric series rGr is defined by
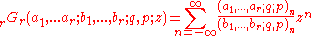
Definitions of additive elliptic hypergeometric series
The elliptic numbers are defined by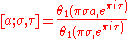
where the Jacobi theta function is defined by

The additive elliptic shifted factorials are defined by
The additive theta hypergeometric series r+1er is defined by

The additive very-well-poised theta hypergeometric series r+1vr is defined by