Energy-momentum relation
Encyclopedia
In special relativity
, the energy-momentum relation is a relation between the energy
, momentum
and the mass
of a body: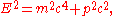
where c is the speed of light
,
is total energy, 
is invariant mass
, and
is momentum.
For a body in its rest frame, the momentum is zero, so the equation simplifies to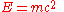
If the object is massless then the energy momentum relation reduces to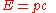
as is the case for a photon
.
In natural units
the energy-momentum relation can be expressed as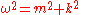
where
is angular frequency
,
is rest mass and 
is wave number.
In Minkowski space
, energy and momentum (the latter multiplied by a factor of c) can be seen as two components of a Minkowski four-vector
. The norm
of this vector is equal to the square of the rest mass of the body, which is a Lorentz
invariant
quantity and hence is independent of the frame of reference
.
When working in units where c = 1, known as the natural unit system, the energy-momentum equation reduces to
In particle physics
, energy is typically given in units of electron volts (eV), momentum in units of eV/c, and mass in units of eV/c2. In electromagnetism, and because of relativistic invariance, it is useful to have the electric field E and the magnetic field B in the same unit (gauss), using the cgs (gaussian) system of units, where energy is given in units of erg
, momentum in g.cm/s and mass in gram
s.
Energy may also in theory be expressed in units of grams, though in practice it requires a large amount of energy to be equivalent to masses in this range. For example, the first atomic bomb liberated about 1 gram of heat, and the largest thermonuclear bombs have generated a kilogram or more of heat. Energies of thermonuclear bombs are usually given in tens of kilotons and megatons referring to the energy liberated by exploding that amount of trinitrotoluene (TNT).
Special relativity
Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...
, the energy-momentum relation is a relation between the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
, momentum
Momentum
In classical mechanics, linear momentum or translational momentum is the product of the mass and velocity of an object...
and the mass
Mass
Mass can be defined as a quantitive measure of the resistance an object has to change in its velocity.In physics, mass commonly refers to any of the following three properties of matter, which have been shown experimentally to be equivalent:...
of a body:
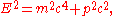
where c is the speed of light
Speed of light
The speed of light in vacuum, usually denoted by c, is a physical constant important in many areas of physics. Its value is 299,792,458 metres per second, a figure that is exact since the length of the metre is defined from this constant and the international standard for time...
,
is total energy, is invariant massInvariant mass
The invariant mass, rest mass, intrinsic mass, proper mass or just mass is a characteristic of the total energy and momentum of an object or a system of objects that is the same in all frames of reference related by Lorentz transformations...
, and
is momentum.For a body in its rest frame, the momentum is zero, so the equation simplifies to
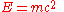
If the object is massless then the energy momentum relation reduces to
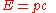
as is the case for a photon
Photon
In physics, a photon is an elementary particle, the quantum of the electromagnetic interaction and the basic unit of light and all other forms of electromagnetic radiation. It is also the force carrier for the electromagnetic force...
.
In natural units
Natural units
In physics, natural units are physical units of measurement based only on universal physical constants. For example the elementary charge e is a natural unit of electric charge, or the speed of light c is a natural unit of speed...
the energy-momentum relation can be expressed as
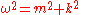
where
is angular frequencyAngular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
,
is rest mass and is wave number.In Minkowski space
Minkowski space
In physics and mathematics, Minkowski space or Minkowski spacetime is the mathematical setting in which Einstein's theory of special relativity is most conveniently formulated...
, energy and momentum (the latter multiplied by a factor of c) can be seen as two components of a Minkowski four-vector
Four-vector
In the theory of relativity, a four-vector is a vector in a four-dimensional real vector space, called Minkowski space. It differs from a vector in that it can be transformed by Lorentz transformations. The usage of the four-vector name tacitly assumes that its components refer to a standard basis...
. The norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
of this vector is equal to the square of the rest mass of the body, which is a Lorentz
Lorentz
Lorentz is a name derived from the Roman surname, Laurentius, which mean "from Laurentum". It is the German form of Laurence.Lorentz may refer to:- Literature :* Friedrich Lorentz, author of works on the Pomeranian language...
invariant
Invariant (physics)
In mathematics and theoretical physics, an invariant is a property of a system which remains unchanged under some transformation.-Examples:In the current era, the immobility of polaris under the diurnal motion of the celestial sphere is a classical illustration of physical invariance.Another...
quantity and hence is independent of the frame of reference
Frame of reference
A frame of reference in physics, may refer to a coordinate system or set of axes within which to measure the position, orientation, and other properties of objects in it, or it may refer to an observational reference frame tied to the state of motion of an observer.It may also refer to both an...
.
When working in units where c = 1, known as the natural unit system, the energy-momentum equation reduces to
In particle physics
Particle physics
Particle physics is a branch of physics that studies the existence and interactions of particles that are the constituents of what is usually referred to as matter or radiation. In current understanding, particles are excitations of quantum fields and interact following their dynamics...
, energy is typically given in units of electron volts (eV), momentum in units of eV/c, and mass in units of eV/c2. In electromagnetism, and because of relativistic invariance, it is useful to have the electric field E and the magnetic field B in the same unit (gauss), using the cgs (gaussian) system of units, where energy is given in units of erg
Erg
An erg is the unit of energy and mechanical work in the centimetre-gram-second system of units, symbol "erg". Its name is derived from the Greek ergon, meaning "work"....
, momentum in g.cm/s and mass in gram
Gram
The gram is a metric system unit of mass....
s.
Energy may also in theory be expressed in units of grams, though in practice it requires a large amount of energy to be equivalent to masses in this range. For example, the first atomic bomb liberated about 1 gram of heat, and the largest thermonuclear bombs have generated a kilogram or more of heat. Energies of thermonuclear bombs are usually given in tens of kilotons and megatons referring to the energy liberated by exploding that amount of trinitrotoluene (TNT).
See also
- Mass-energy equivalenceMass-energy equivalenceIn physics, mass–energy equivalence is the concept that the mass of a body is a measure of its energy content. In this concept, mass is a property of all energy, and energy is a property of all mass, and the two properties are connected by a constant...
- Four-momentumFour-momentumIn special relativity, four-momentum is the generalization of the classical three-dimensional momentum to four-dimensional spacetime. Momentum is a vector in three dimensions; similarly four-momentum is a four-vector in spacetime...