Eutactic star
Encyclopedia
In Euclidean geometry
, a eutactic star is a geometrical figure in a Euclidean space
. A star is a figure consisting of any number of opposing pairs of vectors (or arms) issuing from a central origin. A star is eutactic if it is the orthogonal projection
of a cross-polytope
from a higher-dimensional space onto a subspace
. Such stars were "eutactic" – meaning "well-situated" or "well-arranged" – by because, for a common scalar multiple
, their vectors are projections of an orthonormal basis
.
equal vectors b1, ..., bs issuing from a particular origin in Euclidean s-dimensional space. The configuration of 2s vectors in the s-dimensional space B = ±b1, ... , ±bs is known as a cross. Given these definitions, a eutactic star is, concisely, a star produced by the orthogonal projection of a cross.
An equivalent definition, first mentioned by Schläfli, stipulates that a star is eutactic if a constant ζ exists such that
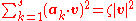
for every vector v. The existence of such a constant requires that the sum of the squares of the orthogonal projections of A on a line be equal in all directions. In general,
A normalised eutactic star is a projected cross composed of unit vectors. Eutactic stars are often considered in n = 3 dimensions because of their connection with the study of regular polyhedra.
defined for vectors x by
where the aj form any collection of s vectors in the n-dimensional Euclidean space. Hadwiger's principal theorem states that the vectors ±a1, ..., ±as form a eutactic star if and only if
there is a constant ζ such that Tx = ζx for every x. The vectors form a normalized eutactic star precisely when T is the identity operator – when ζ = 1.
Equivalently, the star is normalized eutactic if and only if the matrix
A = [a1 ... as], whose columns are the vectors ak, has orthonormal rows. A proof may be given in one direction by completing the rows of this matrix to an orthonormal basis
of
, and in the other by orthogonally projecting onto the n-dimensional subspace spanned by the first n Cartesian coordinate vectors.
Hadwiger's theorem implies the equivalence of Schläfli's stipulation and the geometrical definition of a eutactic star, by the polarization identity
. Furthermore, both Schläfli's identity and Hadwiger's theorem give the same value of the constant ζ.
s and groups
of orthogonal transformations. Schläfli showed early on that the vectors from the center of any regular polytope to its vertices form a eutactic star. Brauer and Coxeter proved the following generalization:
An irreducible group here means a group that does not leave any nontrivial proper subspace invariant (see irreducible representation). Since the set theoretic union of two eutactic stars is itself eutactic (a consequence of Hadwiger's principal theorem), it can be concluded that, in general:
Eutactic stars may be used to validate the eutaxy of any form in general. According to H. S. M. Coxeter: "A form is eutactic if and only if its minimal vectors are parallel
to the vectors of a eutactic star."
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, a eutactic star is a geometrical figure in a Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
. A star is a figure consisting of any number of opposing pairs of vectors (or arms) issuing from a central origin. A star is eutactic if it is the orthogonal projection
Projection (mathematics)
Generally speaking, in mathematics, a projection is a mapping of a set which is idempotent, which means that a projection is equal to its composition with itself. A projection may also refer to a mapping which has a left inverse. Bot notions are strongly related, as follows...
of a cross-polytope
Cross-polytope
In geometry, a cross-polytope, orthoplex, hyperoctahedron, or cocube is a regular, convex polytope that exists in any number of dimensions. The vertices of a cross-polytope are all the permutations of . The cross-polytope is the convex hull of its vertices...
from a higher-dimensional space onto a subspace
Euclidean subspace
In linear algebra, a Euclidean subspace is a set of vectors that is closed under addition and scalar multiplication. Geometrically, a subspace is a flat in n-dimensional Euclidean space that passes through the origin...
. Such stars were "eutactic" – meaning "well-situated" or "well-arranged" – by because, for a common scalar multiple
Scalar (mathematics)
In linear algebra, real numbers are called scalars and relate to vectors in a vector space through the operation of scalar multiplication, in which a vector can be multiplied by a number to produce another vector....
, their vectors are projections of an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
.
Definition
A star is here defined as a set of 2s vectors A = ±a1, ..., ±as issuing from a particular origin in a Euclidean space of dimension n ≤ s. A star is eutactic if the ai are the projections onto n dimensions of a set of mutually perpendicularPerpendicular
In geometry, two lines or planes are considered perpendicular to each other if they form congruent adjacent angles . The term may be used as a noun or adjective...
equal vectors b1, ..., bs issuing from a particular origin in Euclidean s-dimensional space. The configuration of 2s vectors in the s-dimensional space B = ±b1, ... , ±bs is known as a cross. Given these definitions, a eutactic star is, concisely, a star produced by the orthogonal projection of a cross.
An equivalent definition, first mentioned by Schläfli, stipulates that a star is eutactic if a constant ζ exists such that
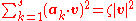
for every vector v. The existence of such a constant requires that the sum of the squares of the orthogonal projections of A on a line be equal in all directions. In general,
A normalised eutactic star is a projected cross composed of unit vectors. Eutactic stars are often considered in n = 3 dimensions because of their connection with the study of regular polyhedra.
Hadwiger's principal theorem
Let T be the symmetric linear transformationLinear transformation
In mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
defined for vectors x by
where the aj form any collection of s vectors in the n-dimensional Euclidean space. Hadwiger's principal theorem states that the vectors ±a1, ..., ±as form a eutactic star if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
there is a constant ζ such that Tx = ζx for every x. The vectors form a normalized eutactic star precisely when T is the identity operator – when ζ = 1.
Equivalently, the star is normalized eutactic if and only if the matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
A = [a1 ... as], whose columns are the vectors ak, has orthonormal rows. A proof may be given in one direction by completing the rows of this matrix to an orthonormal basis
Orthonormal basis
In mathematics, particularly linear algebra, an orthonormal basis for inner product space V with finite dimension is a basis for V whose vectors are orthonormal. For example, the standard basis for a Euclidean space Rn is an orthonormal basis, where the relevant inner product is the dot product of...
of
, and in the other by orthogonally projecting onto the n-dimensional subspace spanned by the first n Cartesian coordinate vectors.Hadwiger's theorem implies the equivalence of Schläfli's stipulation and the geometrical definition of a eutactic star, by the polarization identity
Polarization identity
In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let \|x\| \, denote the norm of vector x and \langle x, \ y \rangle \, the inner product of vectors x and y...
. Furthermore, both Schläfli's identity and Hadwiger's theorem give the same value of the constant ζ.
Applications
Eutactic stars are useful largely because of their relationship with the geometry of polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s and groups
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
of orthogonal transformations. Schläfli showed early on that the vectors from the center of any regular polytope to its vertices form a eutactic star. Brauer and Coxeter proved the following generalization:
A star is eutactic if and only if it is transformed to itself by some irreducible group of orthogonal transformations that acts transitively on pairs of opposite vectors.
An irreducible group here means a group that does not leave any nontrivial proper subspace invariant (see irreducible representation). Since the set theoretic union of two eutactic stars is itself eutactic (a consequence of Hadwiger's principal theorem), it can be concluded that, in general:
A star is eutactic if and only if it is transformed to itself by some irreducible group of orthogonal transformations.
Eutactic stars may be used to validate the eutaxy of any form in general. According to H. S. M. Coxeter: "A form is eutactic if and only if its minimal vectors are parallel
Parallel (geometry)
Parallelism is a term in geometry and in everyday life that refers to a property in Euclidean space of two or more lines or planes, or a combination of these. The assumed existence and properties of parallel lines are the basis of Euclid's parallel postulate. Two lines in a plane that do not...
to the vectors of a eutactic star."