Evaluating sums
Encyclopedia
In mathematics
, a series
is the sum of the elements of a sequence. This article mentions a few common series and how to compute their values (or prove that they do not converge). This gives more derivations than the list of mathematical series elsewhere in Wikipedia.
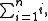
the sum of the first n natural number
s, for any natural number n. Since it is finite, it converges, and its value can be determined using the following technique. We can rewrite the sum by "counting down" rather than "counting up"; that is, if the above series is S, then
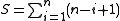
If we now add both expressions we have
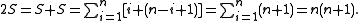
Therefore we get the fundamental identity
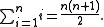
(This formula breaks down in some instances--- for example when performing modular arithmetic
with modulus 2, this formula is nonsensical; however, in that case the sum can easily be evaluated by inspection since the terms alternate between 0 and 1).
Other arithmetic series may be computed using this calculation as a base. Given any two numbers a, d (which may be integral, real, complex, or in fact members of any abelian group
at all), we may define an arithmetic progression with initial term a and difference d, whose general term is
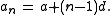
For a fixed integer n, we can form the arithmetic series
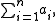
the sum of the first n terms of this progression. If we substitute the definition of ai and use the linearity of the sum, the computation reduces to one we have just done:
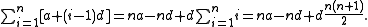
This simplifies (using the definition of an) to
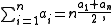
the average of the outer terms of the progression multiplied by the number of terms.
; a is the initial term, and r is the ratio between successive terms. Then the series is
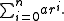
To evaluate this series (again denoted S), a simple cancellation trick is used: if we multiply the series by r and subtract from the original, we get
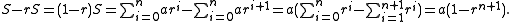
Thus we get the fundamental relation
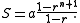
(Again, to be perfectly precise we must have r not equal to 1; in this case, the sum is easily evaluated by inspection since each power of i is also equal to 1).
If (as is usual) we are working in the real or complex numbers, and if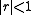
, then we can take the limit as n approaches infinity. This yields the infinite series
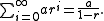
Of course, the right-hand side is valid for any number r other than 1, but only when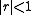
is it equal to the left-hand side. Otherwise, the series diverges (since the terms do not approach 0).
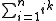
for positive integers k; the arithmetic series is the case for k equal to 1. It follows from an identity of the Bernoulli polynomials
that these sums can be calculated as:
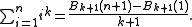
This is not as vacuous as it seems, since the Bernoulli polynomials are well-studied and their coefficients, which are related to the Bernoulli numbers, are easy to calculate.
can be used to find the sum of certain series which are not obvious at first glance; by their nature, these are generally infinite series. There are several well-known examples:
This is not immediate; the radius of convergence
of the power series for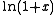
is just 1, and therefore this sum lies on the boundary. To show that the value of the power series is equal to the value of the function requires additional analysis.
Using the binomial theorem
, which is a very special case of the Taylor series (about 1) for the function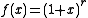
for arbitrary positive real numbers r, we can also obtain
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a series
Series (mathematics)
A series is the sum of the terms of a sequence. Finite sequences and series have defined first and last terms, whereas infinite sequences and series continue indefinitely....
is the sum of the elements of a sequence. This article mentions a few common series and how to compute their values (or prove that they do not converge). This gives more derivations than the list of mathematical series elsewhere in Wikipedia.
Arithmetic series
The prototype of the arithmetic series is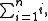the sum of the first n natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s, for any natural number n. Since it is finite, it converges, and its value can be determined using the following technique. We can rewrite the sum by "counting down" rather than "counting up"; that is, if the above series is S, then
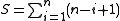
If we now add both expressions we have
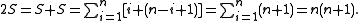
Therefore we get the fundamental identity
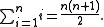
(This formula breaks down in some instances--- for example when performing modular arithmetic
Modular arithmetic
In mathematics, modular arithmetic is a system of arithmetic for integers, where numbers "wrap around" after they reach a certain value—the modulus....
with modulus 2, this formula is nonsensical; however, in that case the sum can easily be evaluated by inspection since the terms alternate between 0 and 1).
Other arithmetic series may be computed using this calculation as a base. Given any two numbers a, d (which may be integral, real, complex, or in fact members of any abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
at all), we may define an arithmetic progression with initial term a and difference d, whose general term is
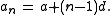
For a fixed integer n, we can form the arithmetic series
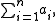
the sum of the first n terms of this progression. If we substitute the definition of ai and use the linearity of the sum, the computation reduces to one we have just done:
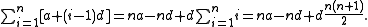
This simplifies (using the definition of an) to
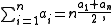
the average of the outer terms of the progression multiplied by the number of terms.
Geometric series
Geometric series, like arithmetic series, can be defined for any numbers (integer, real, complex, or otherwise) a and r. Due to the rules of exponentiation these series tend to be indexed from zeroZeroth
Zero-based numbering is numbering in which the initial element of a sequence is assigned the index 0, rather than the index 1 as is typical in everyday circumstances. Under zero-based numbering, the initial element is sometimes termed the zeroth element, rather than the first element; zeroth is a...
; a is the initial term, and r is the ratio between successive terms. Then the series is
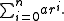
To evaluate this series (again denoted S), a simple cancellation trick is used: if we multiply the series by r and subtract from the original, we get
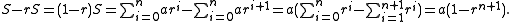
Thus we get the fundamental relation
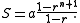
(Again, to be perfectly precise we must have r not equal to 1; in this case, the sum is easily evaluated by inspection since each power of i is also equal to 1).
If (as is usual) we are working in the real or complex numbers, and if
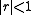, then we can take the limit as n approaches infinity. This yields the infinite series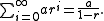Of course, the right-hand side is valid for any number r other than 1, but only when
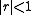is it equal to the left-hand side. Otherwise, the series diverges (since the terms do not approach 0).Higher powers
Other common families of series are sums of powers: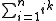for positive integers k; the arithmetic series is the case for k equal to 1. It follows from an identity of the Bernoulli polynomials
Bernoulli polynomials
In mathematics, the Bernoulli polynomials occur in the study of many special functions and in particular the Riemann zeta function and the Hurwitz zeta function. This is in large part because they are an Appell sequence, i.e. a Sheffer sequence for the ordinary derivative operator...
that these sums can be calculated as:
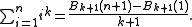
This is not as vacuous as it seems, since the Bernoulli polynomials are well-studied and their coefficients, which are related to the Bernoulli numbers, are easy to calculate.
Applications of Taylor series
Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
can be used to find the sum of certain series which are not obvious at first glance; by their nature, these are generally infinite series. There are several well-known examples:
;
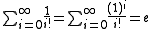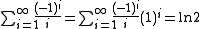
This is not immediate; the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of the power series for
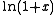is just 1, and therefore this sum lies on the boundary. To show that the value of the power series is equal to the value of the function requires additional analysis.
.
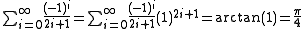Using the binomial theorem
Binomial theorem
In elementary algebra, the binomial theorem describes the algebraic expansion of powers of a binomial. According to the theorem, it is possible to expand the power n into a sum involving terms of the form axbyc, where the exponents b and c are nonnegative integers with , and the coefficient a of...
, which is a very special case of the Taylor series (about 1) for the function
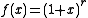for arbitrary positive real numbers r, we can also obtain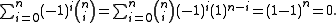See also
- Arithmetic series
- Geometric series
- Taylor seriesTaylor seriesIn mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
- Bernoulli numberBernoulli numberIn mathematics, the Bernoulli numbers Bn are a sequence of rational numbers with deep connections to number theory. They are closely related to the values of the Riemann zeta function at negative integers....