Existential graph
Encyclopedia
An existential graph is a type of diagram
matic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic
as early as 1882, and continued to develop the method until his death in 1914.
Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more than even Peirce could envisage.
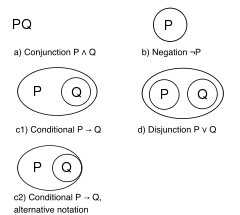The syntax
is:
Any well-formed part of a graph is a subgraph.
The semantics
are:
Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.
The depth of an object is the number of cuts that enclose it.
Rules of inference:
Rules of equivalence:
A proof manipulates a graph by a series of steps, with each step justified by one of the above rules. If a graph can be reduced by steps to the blank page or an empty cut, it is what is now called a tautology
(or the complement thereof). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formula
s of first-order logic
.
. Multiple instances of the same object are linked by a line, called the "line of identity". There are no literal variables
or quantifiers in the sense of first-order logic
. A line of identity connecting two or more predicates can be read as asserting that the predicates share a common variable. The presence of lines of identity requires modifying the alpha rules of Equivalence.
The beta graphs can be read as a system in which all formula are to be taken as closed, because all variables are implicitly quantified. If the "shallowest" part of a line of identity has even (odd) depth, the associated variable is tacitly existentially (universally) quantified.
Zeman (1964) was the first to note that the beta graphs are isomorphic
to first-order logic
with equality (also see Zeman 1967). However, the secondary literature, especially Roberts (1973) and Shin (2002), does not agree on just how this is so. Peirce's writings do not address this question, because first-order logic was first clearly articulated only some years after his death, in the 1928 first edition of David Hilbert
and Wilhelm Ackermann
's Principles of Mathematical Logic.
of modal logic
.
Zeman (1964) was the first to note that straightforward emendations of the gamma graph rules yield the well-known modal logics S4
and S5
. Hence the gamma graphs can be read as a peculiar form of normal modal logic
. This finding of Zeman's has gone unremarked to this day, but we included it in Wikipedia anyway.
ian/ mathematician with Peirce the founder of a major strand of semiotics
. Peirce's graphical logic is but one of his many accomplishments in logic and mathematics. In a series of papers beginning in 1867, and culminating with his classic paper in the 1885 American Journal of Mathematics
, Peirce developed much of the two-element Boolean algebra, propositional calculus, quantification
and the predicate calculus
, and some rudimentary set theory
. Model theorists
consider Peirce the first of their kind. He also extended De Morgan's relation algebra
. He stopped short of metalogic (which eluded even Principia Mathematica
).
But Peirce's evolving semiotic theory led him to doubt the value of logic formulated using conventional linear notation, and to prefer that logic and mathematics be notated in two (or even three) dimensions. His work went beyond Euler's diagrams
and Venn
's revision thereof. Frege's 1879 Begriffsschrift
also employed a two-dimensional notation for logic, but one very different from Peirce's.
Peirce's first published paper on graphical logic (reprinted in Vol. 3 of his Collected Papers) proposed a system dual (in effect) to the alpha existential graphs, called the entitative graph
s. He very soon abandoned this formalism in favor of the existential graphs. The graphical logic went unremarked during his lifetime, and was invariably denigrated or ignored after his death, until the Ph.D. theses by Roberts (1964) and Zeman (1964).
Currently, the chronological critical edition of Peirce's works, the Writings, extends only to 1892. Much of Peirce's work on logical graph
s consists of manuscripts written after that date and still unpublished. Hence our understanding of Peirce's graphical logic is likely to change as the remaining 23 volumes of the chronological edition appear.
Diagram
A diagram is a two-dimensional geometric symbolic representation of information according to some visualization technique. Sometimes, the technique uses a three-dimensional visualization which is then projected onto the two-dimensional surface...
matic or visual notation for logical expressions, proposed by Charles Sanders Peirce, who wrote on graphical logic
Logical graph
A logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
as early as 1882, and continued to develop the method until his death in 1914.
The graphs
Peirce proposed three systems of existential graphs:- alpha, isomorphicIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to sentential logic and the two-element Boolean algebra; - beta, isomorphic to first-order logicFirst-order logicFirst-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with identity, with all formulas closed; - gamma, (nearly) isomorphic to normal modal logicNormal modal logicIn logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
.
Alpha nests in beta and gamma. Beta does not nest in gamma, quantified modal logic being more than even Peirce could envisage.
Alpha
Syntax
In linguistics, syntax is the study of the principles and rules for constructing phrases and sentences in natural languages....
is:
- The blank page;
- Single letters or phrases written anywhere on the page;
- Any graph may be enclosed by a simple closed curve called a cut or sep. A cut can be empty. Cuts can nest and concatenate at will, but must never intersect.
Any well-formed part of a graph is a subgraph.
The semantics
Semantics
Semantics is the study of meaning. It focuses on the relation between signifiers, such as words, phrases, signs and symbols, and what they stand for, their denotata....
are:
- The blank page denotes Truth;
- Letters, phrases, subgraphs, and entire graphs may be True or False;
- To enclose a subgraph with a cut is equivalent to logical negationNegationIn logic and mathematics, negation, also called logical complement, is an operation on propositions, truth values, or semantic values more generally. Intuitively, the negation of a proposition is true when that proposition is false, and vice versa. In classical logic negation is normally identified...
or Boolean complementation. Hence an empty cut denotes False; - All subgraphs within a given cut are tacitly conjoined.
Hence the alpha graphs are a minimalist notation for sentential logic, grounded in the expressive adequacy of And and Not. The alpha graphs constitute a radical simplification of the two-element Boolean algebra and the truth functors.
The depth of an object is the number of cuts that enclose it.
Rules of inference:
- Insertion - Any subgraph may be inserted into an odd numbered depth.
- Erasure - Any subgraph in an even numbered depth may be erased.
Rules of equivalence:
- Double cut - A pair of cuts with nothing between them may be drawn around any subgraph. Likewise two nested cuts with nothing between them may be erased. This rule is equivalent to Boolean involution.
- Iteration/Deiteration – To understand this rule, it is best to view a graph as a tree structureTree structureA tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
having nodeNode (computer science)A node is a record consisting of one or more fields that are links to other nodes, and a data field. The link and data fields are often implemented by pointers or references although it is also quite common for the data to be embedded directly in the node. Nodes are used to build linked, often...
s and ancestorsTree structureA tree structure is a way of representing the hierarchical nature of a structure in a graphical form. It is named a "tree structure" because the classic representation resembles a tree, even though the chart is generally upside down compared to an actual tree, with the "root" at the top and the...
. Any subgraph P in node n may be copied into any node depending on n. Likewise, any subgraph P in node n may be erased if there exists a copy of P in some node ancestral to n (i.e., some node on which n depends). For an equivalent rule in an algebraic context, see C2 in Laws of formLaws of FormLaws of Form is a book by G. Spencer-Brown, published in 1969, that straddles the boundary between mathematics and philosophy...
.
A proof manipulates a graph by a series of steps, with each step justified by one of the above rules. If a graph can be reduced by steps to the blank page or an empty cut, it is what is now called a tautology
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
(or the complement thereof). Graphs that cannot be simplified beyond a certain point are analogues of the satisfiable formula
Formula
In mathematics, a formula is an entity constructed using the symbols and formation rules of a given logical language....
s of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
.
Beta
Peirce notated predicates using intuitive English phrases; the standard notation of contemporary logic, capital Latin letters, may also be employed. A dot asserts the existence of some individual in the domain of discourseDomain of discourse
In the formal sciences, the domain of discourse, also called the universe of discourse , is the set of entities over which certain variables of interest in some formal treatment may range...
. Multiple instances of the same object are linked by a line, called the "line of identity". There are no literal variables
Variable (mathematics)
In mathematics, a variable is a value that may change within the scope of a given problem or set of operations. In contrast, a constant is a value that remains unchanged, though often unknown or undetermined. The concepts of constants and variables are fundamental to many areas of mathematics and...
or quantifiers in the sense of first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
. A line of identity connecting two or more predicates can be read as asserting that the predicates share a common variable. The presence of lines of identity requires modifying the alpha rules of Equivalence.
The beta graphs can be read as a system in which all formula are to be taken as closed, because all variables are implicitly quantified. If the "shallowest" part of a line of identity has even (odd) depth, the associated variable is tacitly existentially (universally) quantified.
Zeman (1964) was the first to note that the beta graphs are isomorphic
Isomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
to first-order logic
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
with equality (also see Zeman 1967). However, the secondary literature, especially Roberts (1973) and Shin (2002), does not agree on just how this is so. Peirce's writings do not address this question, because first-order logic was first clearly articulated only some years after his death, in the 1928 first edition of David Hilbert
David Hilbert
David Hilbert was a German mathematician. He is recognized as one of the most influential and universal mathematicians of the 19th and early 20th centuries. Hilbert discovered and developed a broad range of fundamental ideas in many areas, including invariant theory and the axiomatization of...
and Wilhelm Ackermann
Wilhelm Ackermann
Wilhelm Friedrich Ackermann was a German mathematician best known for the Ackermann function, an important example in the theory of computation....
's Principles of Mathematical Logic.
Gamma
Add to the syntax of alpha a second kind of simple closed curve, written using a dashed rather than a solid line. Peirce proposed rules for this second style of cut, which can be read as the primitive unary operatorUnary operation
In mathematics, a unary operation is an operation with only one operand, i.e. a single input. Specifically, it is a functionf:\ A\to Awhere A is a set. In this case f is called a unary operation on A....
of modal logic
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
.
Zeman (1964) was the first to note that straightforward emendations of the gamma graph rules yield the well-known modal logics S4
Modal logic
Modal logic is a type of formal logic that extends classical propositional and predicate logic to include operators expressing modality. Modals — words that express modalities — qualify a statement. For example, the statement "John is happy" might be qualified by saying that John is...
and S5
S5 (modal logic)
In logic and philosophy, S5 is one of five systems of modal logic proposed byClarence Irving Lewis and Cooper Harold Langford in their 1932 book Symbolic Logic.It is a normal modal logic, and one of the oldest systems of modal logic of any kind....
. Hence the gamma graphs can be read as a peculiar form of normal modal logic
Normal modal logic
In logic, a normal modal logic is a set L of modal formulas such that L contains:* All propositional tautologies;* All instances of the Kripke schema: \Box\toand it is closed under:...
. This finding of Zeman's has gone unremarked to this day, but we included it in Wikipedia anyway.
Peirce's role
The existential graphs are a curious offspring of Peirce the logicLogic
In philosophy, Logic is the formal systematic study of the principles of valid inference and correct reasoning. Logic is used in most intellectual activities, but is studied primarily in the disciplines of philosophy, mathematics, semantics, and computer science...
ian/ mathematician with Peirce the founder of a major strand of semiotics
Semiotics
Semiotics, also called semiotic studies or semiology, is the study of signs and sign processes , indication, designation, likeness, analogy, metaphor, symbolism, signification, and communication...
. Peirce's graphical logic is but one of his many accomplishments in logic and mathematics. In a series of papers beginning in 1867, and culminating with his classic paper in the 1885 American Journal of Mathematics
American Journal of Mathematics
The American Journal of Mathematics is a bimonthly mathematics journal published by the Johns Hopkins University Press.- History :The American Journal of Mathematics is the oldest continuously-published mathematical journal in the United States, established in 1878 at the Johns Hopkins University...
, Peirce developed much of the two-element Boolean algebra, propositional calculus, quantification
Quantification
Quantification has several distinct senses. In mathematics and empirical science, it is the act of counting and measuring that maps human sense observations and experiences into members of some set of numbers. Quantification in this sense is fundamental to the scientific method.In logic,...
and the predicate calculus
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
, and some rudimentary set theory
Set theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
. Model theorists
Model theory
In mathematics, model theory is the study of mathematical structures using tools from mathematical logic....
consider Peirce the first of their kind. He also extended De Morgan's relation algebra
Relation algebra
In mathematics and abstract algebra, a relation algebra is a residuated Boolean algebra expanded with an involution called converse, a unary operation...
. He stopped short of metalogic (which eluded even Principia Mathematica
Principia Mathematica
The Principia Mathematica is a three-volume work on the foundations of mathematics, written by Alfred North Whitehead and Bertrand Russell and published in 1910, 1912, and 1913...
).
But Peirce's evolving semiotic theory led him to doubt the value of logic formulated using conventional linear notation, and to prefer that logic and mathematics be notated in two (or even three) dimensions. His work went beyond Euler's diagrams
Euler diagram
An Euler diagram is a diagrammatic means of representing sets and their relationships. The first use of "Eulerian circles" is commonly attributed to Swiss mathematician Leonhard Euler . They are closely related to Venn diagrams....
and Venn
Venn
Venn may mean:* Blair Venn, Australian actor* John Venn , several people* Henry Venn the elder, , English evangelical minister...
's revision thereof. Frege's 1879 Begriffsschrift
Begriffsschrift
Begriffsschrift is a book on logic by Gottlob Frege, published in 1879, and the formal system set out in that book...
also employed a two-dimensional notation for logic, but one very different from Peirce's.
Peirce's first published paper on graphical logic (reprinted in Vol. 3 of his Collected Papers) proposed a system dual (in effect) to the alpha existential graphs, called the entitative graph
Entitative graph
An entitative graph is an element of the diagrammatic syntax for logic that Charles Sanders Peirce developed under the name of qualitative logic beginning in the 1880's, taking the coverage of the formalism only as far as the propositional or sentential aspects of logic are concerned...
s. He very soon abandoned this formalism in favor of the existential graphs. The graphical logic went unremarked during his lifetime, and was invariably denigrated or ignored after his death, until the Ph.D. theses by Roberts (1964) and Zeman (1964).
Primary literature
- 1931-35 & 1958. The Collected Papers of Charles Sanders Peirce. Volume 4, Book II: "Existential Graphs", consists of paragraphs 347–584, which constitute the locus citandum for the existential graphs.
- Paragraphs 347–349 (II.1.1. "Logical Diagram")—Peirce's definition "Logical Diagram (or Graph)" in BaldwinJames Mark BaldwinJames Mark Baldwin was an American philosopher and psychologist who was educated at Princeton under the supervision of Scottish philosopher James McCosh and who was one of the founders of the Department of Psychology at the university...
's Dictionary of Philosophy and Psychology (1902), v. 2, p. 28. Classics in the History of Psychology Eprint. - Paragraphs 350–371 (II.1.2. "Of Euler's Diagrams")—from "Graphs" (manuscript 479) c. 1903.
- Paragraphs 372–584 Eprint.
- Paragraphs 372–393 (II.2. "Symbolic Logic")—Peirce's part of "Symbolic Logic" in Baldwin's Dictionary of Philosophy and Psychology (1902) v. 2, pp. 645–650, beginning (near second column's top) with "If symbolic logic be defined...". Paragraph 393 (Baldwin's DPP2 p. 650) is by Peirce and Christine Ladd-FranklinChristine Ladd-FranklinChristine Ladd-Franklin was the first American woman psychologist, logician, and mathematician.-Early Life and Early Education:...
("C.S.P., C.L.F."). - Paragraphs 394–417 (II.3. "Existential Graphs")—from Peirce's pamphlet A Syllabus of Certain Topics of Logic, pp. 15–23, Alfred Mudge & Son, Boston (1903).
- Paragraphs 418–509 (II.4. "On Existential Graphs, Euler's Diagrams, and Logical Algebra")—from "Logical Tracts, No. 2" (manuscript 492), c. 1903.
- Paragraphs 510–529 (II.5. "The Gamma Part of Existential Graphs")—from "Lowell Lectures of 1903," Lecture IV (manuscript 467).
- Paragraphs 530–572 (II.6.)—"Prolegomena To an Apology For Pragmaticism" (1906), The MonistThe MonistThe Monist: An International Quarterly Journal of General Philosophical Inquiry is an American academic journal in the field of philosophy. It was founded in October 1890 by Edward C. Hegeler, making it one of the longest-established journals in philosophy...
, v. XVI, n. 4, pp. 492-546. - Paragraphs 573–584 (II.7. "An Improvement on the Gamma Graphs")—from "For the National Academy of Science, 1906 April Meeting in Washington" (manuscript 490).
- Paragraphs 347–349 (II.1.1. "Logical Diagram")—Peirce's definition "Logical Diagram (or Graph)" in Baldwin
- 1992. "Lecture Three: The Logic of Relatives", Reasoning and the Logic of Things, pp. 146–64. Ketner, Kenneth Laine (editing and introduction), and Hilary PutnamHilary PutnamHilary Whitehall Putnam is an American philosopher, mathematician and computer scientist, who has been a central figure in analytic philosophy since the 1960s, especially in philosophy of mind, philosophy of language, philosophy of mathematics, and philosophy of science...
(commentary). Harvard University PressHarvard University PressHarvard University Press is a publishing house established on January 13, 1913, as a division of Harvard University, and focused on academic publishing. In 2005, it published 220 new titles. It is a member of the Association of American University Presses. Its current director is William P...
. Peirce's 1898 lectures in Cambridge, Massachusetts. - 1977, 2001. Semiotic and Significs: The Correspondence between C.S. Peirce and Victoria Lady Welby. Hardwick, C.S., ed. Lubbock TX: Texas Tech University Press. 2nd edition 2001.
- A transcription of Peirce's MS 514 (1909), edited with commentary by John Sowa.
Currently, the chronological critical edition of Peirce's works, the Writings, extends only to 1892. Much of Peirce's work on logical graph
Logical graph
A logical graph is a special type of diagramatic structure in any one of several systems of graphical syntax that Charles Sanders Peirce developed for logic....
s consists of manuscripts written after that date and still unpublished. Hence our understanding of Peirce's graphical logic is likely to change as the remaining 23 volumes of the chronological edition appear.
Secondary literature
- Hammer, Eric M. (1998), "Semantics for Existential Graphs," Journal of Philosophical Logic 27: 489-503.
- Ketner, Kenneth Laine
- (1981), "The Best Example of Semiosis and Its Use in Teaching Semiotics", American Journal of Semiotics v. I, n. 1-2, pp. 47-83. Article is an introduction to existential graphs.
- (1990), Elements of Logic: An Introduction to Peirce's Existential Graphs, Texas Tech University Press, Lubbock, TX, 99 pages, spiral-bound.
- Roberts, Don D.
- (1964), "Existential Graphs and Natural Deduction" in Moore, E. C., and Robin, R. S., eds., Studies in the Philosophy of C. S. Peirce, 2nd series. Amherst MA: University of Massachusetts Press. The first publication to show any sympathy and understanding for Peirce's graphical logic.
- (1973). The Existential Graphs of C.S. Peirce. John Benjamins. An outgrowth of his 1963 thesis.
- Shin, Sun-Joo (2002), The Iconic Logic of Peirce's Graphs. MIT Press.
- Zeman, J. J.
- (1964), The Graphical Logic of C.S. Peirce. Unpublished Ph.D. thesis submitted to the University of ChicagoUniversity of ChicagoThe University of Chicago is a private research university in Chicago, Illinois, USA. It was founded by the American Baptist Education Society with a donation from oil magnate and philanthropist John D. Rockefeller and incorporated in 1890...
. - (1967), "A System of Implicit Quantification," Journal of Symbolic Logic 32: 480-504.
- (1964), The Graphical Logic of C.S. Peirce. Unpublished Ph.D. thesis submitted to the University of Chicago
External links
- Stanford Encyclopedia of PhilosophyStanford Encyclopedia of PhilosophyThe Stanford Encyclopedia of Philosophy is a freely-accessible online encyclopedia of philosophy maintained by Stanford University. Each entry is written and maintained by an expert in the field, including professors from over 65 academic institutions worldwide...
: Peirce's Logic by Eric Hammer. Employs parentheses notation. - Dau, Frithjof, Peirce's Existential Graphs --- Readings and Links. An annotated bibliography on the existential graphs.
- Gottschall, Christian, Proof Builder — Java applet for deriving Alpha graphs.
- Liu, Xin-Wen, "The literature of C.S. Peirce’s Existential Graphs" (via Wayback Machine), Institute of Philosophy, Chinese Academy of Social Sciences, Beijing, PRC.
- Sowa, John F., "Laws, Facts, and Contexts: Foundations for Multimodal Reasoning" accessdate=2009-10-23 Existential graphs and conceptual graphConceptual graphConceptual graphs are a formalism for knowledge representation. In the first published paper on CGs, John F. Sowa used them to represent the conceptual schemas used in database systems...
s. - Van Heuveln, Bram, "Existential Graphs." Dept. of Cognitive Science, Rensselaer Polytechnic InstituteRensselaer Polytechnic InstituteStephen Van Rensselaer established the Rensselaer School on November 5, 1824 with a letter to the Rev. Dr. Samuel Blatchford, in which van Rensselaer asked Blatchford to serve as the first president. Within the letter he set down several orders of business. He appointed Amos Eaton as the school's...
. Alpha only. - Zeman, Jay J., "Existential Graphs". With four online papers by Peirce.