F(R) gravity
Encyclopedia
f gravity is a type of modified gravity theory first proposed in 1970
by Buchdahl as a generalisation of Einstein's
General Relativity
. Although it is an active field of research, there are known problems with the theory. It has the potential, in principle, to explain the accelerated expansion
of the Universe without adding unknown forms of dark energy
or dark matter
.
of the Einstein-Hilbert action
:
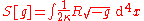
to
where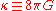
, 
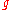is the determinant of the metric tensor
and 
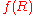is some function of the Ricci Curvature
.
(see the article for more details) but there are also some important differences.
The variation of the determinant is as always: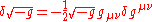
The Ricci scalar is defined as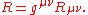
Therefore, its variation with respect to the inverse metric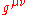
is given by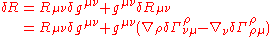
For the second step see the article about the Einstein-Hilbert action
. Now, since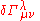
is actually the difference of two connections, it should transform as a tensor. Therefore, it can be written as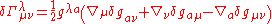
and substituting in the equation above one finds: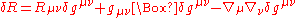
where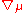
is the covariant derivative
and
is the D'Alembert operator defined as 
.
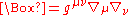Now the variation in the action reads: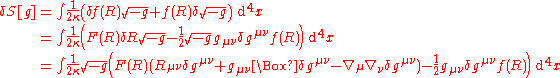
where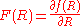
. Doing integration by parts on the second and third terms we get: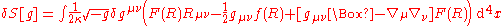
By demanding that the action remains invariant under variations of the metric, ie
, one obtains the field equations:
where
is the energy-momentum tensor defined as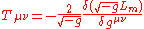
where
is the matter Lagrangian.
we can find the generalized Friedmann equations
to be (in units where
):
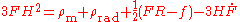
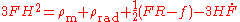
where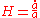
, the dot is the derivative with respect to the cosmic time 
and the terms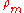 
, 
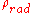represent the matter and radiation densities respectively and satisfy the continuity equations: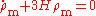
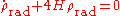
is time and scale dependent. To see this, add a small scalar perturbation to the metric (in the conformal Newtonian gauge):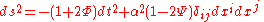
where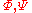
are the Newtonian potentials and use the field equations to first order. After some lengthy calculations, one can define a Poisson equation in the Fourier space and attribute the extra terms that appear on the right hand side to an effective gravitational constant 
.
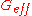Doing so, we get the gravitational potential (valid in sub-horizon scales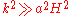
):
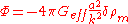where 
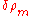is a perturbation in the matter density and 
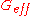is: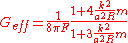
and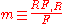
(helicities ±2) and the third (scalar) is coming from the fact that if we take into account a conformal transformation, the fourth order theory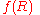
becomes General Relativity
plus a scalar field
. To see this, identify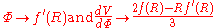
and use the field equations mentioned above to get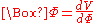
Working to first order of perturbation theory: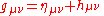
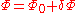
and after some tedious algebra, one can solve for the metric perturbation, which corresponds to the gravitational waves: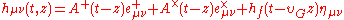
where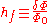
and
is the group velocity
of a wave packet
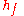centered in momentum 
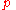as 
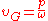. The first two terms correspond to the usual from General Relativity gravitational waves while the third corresponds to the new massive polarization mode of 
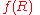theories, which moves at a speed 
(in units where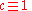 
.
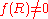for all R, let V(Φ) be the Legendre transform of f(R) so that 
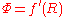and 
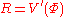. Then,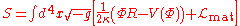
We get the Euler-Lagrange equations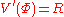
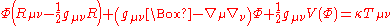
Eliminating Φ, we get exactly the same equations as before. However, the equations we do have are only second order in the derivatives, instead of fourth order.
We are currently working with the Jordan frame. By performing a conformal rescaling
, we get to the Einstein frame.
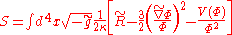
after integrating by parts.
Define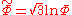
.
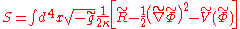
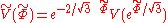
This is none other an ordinary general relativity coupled to a real scalar field! Trying to use f(R) theories to describe the accelerating universe is practically equivalent to using quintessence
.
Due to the structure of the theory, however, Palatini f(R) theories appear to be in conflict with the Standard Model, may violate Solar system experiments, and seem to create unwanted singularities.
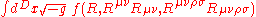
coupling involving invariants of the Ricci tensor and the Weyl tensor
. Special cases are f(R) gravity, conformal gravity, Gauss-Bonnet gravity and Lovelock gravity. It is suggested to consider dependency to the covariant derivative
of the Riemann tensor in order to resolve more problems. Notice that with any nontrivial tensorial dependence, we typically have additional massive spin-2 degrees of freedom, in addition to the massless graviton and a massive scalar. An exception is Gauss-Bonnet gravity where the fourth order terms for the spin-2 components cancel out.
by Buchdahl as a generalisation of Einstein's
Albert Einstein
Albert Einstein was a German-born theoretical physicist who developed the theory of general relativity, effecting a revolution in physics. For this achievement, Einstein is often regarded as the father of modern physics and one of the most prolific intellects in human history...
General Relativity
General relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
. Although it is an active field of research, there are known problems with the theory. It has the potential, in principle, to explain the accelerated expansion
Accelerating universe
The accelerating universe is the observation that the universe appears to be expanding at an increasing rate, which in formal terms means that the cosmic scale factor a has a positive second derivative, implying that the velocity at which a given galaxy is receding from us should be continually...
of the Universe without adding unknown forms of dark energy
Dark energy
In physical cosmology, astronomy and celestial mechanics, dark energy is a hypothetical form of energy that permeates all of space and tends to accelerate the expansion of the universe. Dark energy is the most accepted theory to explain recent observations that the universe appears to be expanding...
or dark matter
Dark matter
In astronomy and cosmology, dark matter is matter that neither emits nor scatters light or other electromagnetic radiation, and so cannot be directly detected via optical or radio astronomy...
.
Introduction
In f(R) gravity, one seeks to generalise the LagrangianLagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
of the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
:
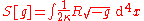
to
where
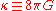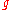, is the determinant of the metric tensorMetric tensor
In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...
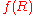and is some function of the Ricci CurvatureScalar curvature
In Riemannian geometry, the scalar curvature is the simplest curvature invariant of a Riemannian manifold. To each point on a Riemannian manifold, it assigns a single real number determined by the intrinsic geometry of the manifold near that point...
.
Derivation of field equations
In metric f(R) gravity, one arrives at the field equations by varying with respect to the metric and not treating the connection independently. For completeness we will now briefly mention the basic steps of the variation of the action. The main steps are the same as in the case of the variation of the Einstein-Hilbert actionEinstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
(see the article for more details) but there are also some important differences.
The variation of the determinant is as always:
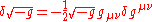
The Ricci scalar is defined as
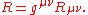
Therefore, its variation with respect to the inverse metric
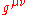is given by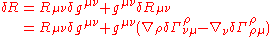For the second step see the article about the Einstein-Hilbert action
Einstein-Hilbert action
The Einstein–Hilbert action in general relativity is the action that yields the Einstein's field equations through the principle of least action...
. Now, since
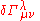is actually the difference of two connections, it should transform as a tensor. Therefore, it can be written as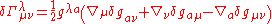and substituting in the equation above one finds:
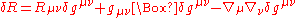
where
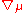is the covariant derivativeCovariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
and
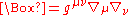is the D'Alembert operator defined as .Now the variation in the action reads:
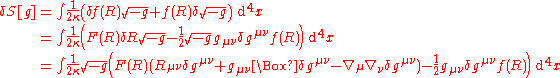
where
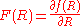. Doing integration by parts on the second and third terms we get: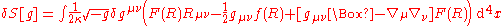By demanding that the action remains invariant under variations of the metric, ie
, one obtains the field equations:where
is the energy-momentum tensor defined as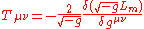where
is the matter Lagrangian.The generalized Friedmann equations
Assuming a Robertson-Walker metric with scale factor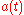 we can find the generalized Friedmann equationsFriedmann equations
The Friedmann equations are a set of equations in physical cosmology that govern the expansion of space in homogeneous and isotropic models of the universe within the context of general relativity...
to be (in units where
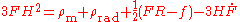
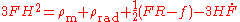
):where
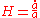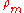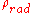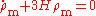
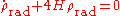
, the dot is the derivative with respect to the cosmic time and the terms , represent the matter and radiation densities respectively and satisfy the continuity equations:Modified Newton's constant
An interesting feature of these theories is the fact that the gravitational constantGravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
is time and scale dependent. To see this, add a small scalar perturbation to the metric (in the conformal Newtonian gauge):
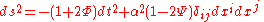
where
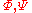are the Newtonian potentials and use the field equations to first order. After some lengthy calculations, one can define a Poisson equation in the Fourier space and attribute the extra terms that appear on the right hand side to an effective gravitational constant 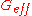.Doing so, we get the gravitational potential (valid in sub-horizon scales
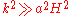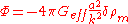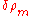): where is a perturbation in the matter density and 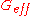is: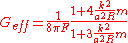and
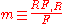
Massive gravitational waves
This class of theories when linearized exhibits three polarization modes for the gravitational waves, of which two correspond to the massless gravitonGraviton
In physics, the graviton is a hypothetical elementary particle that mediates the force of gravitation in the framework of quantum field theory. If it exists, the graviton must be massless and must have a spin of 2...
(helicities ±2) and the third (scalar) is coming from the fact that if we take into account a conformal transformation, the fourth order theory
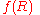becomes General RelativityGeneral relativity
General relativity or the general theory of relativity is the geometric theory of gravitation published by Albert Einstein in 1916. It is the current description of gravitation in modern physics...
plus a scalar field
Scalar field
In mathematics and physics, a scalar field associates a scalar value to every point in a space. The scalar may either be a mathematical number, or a physical quantity. Scalar fields are required to be coordinate-independent, meaning that any two observers using the same units will agree on the...
. To see this, identify
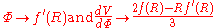
and use the field equations mentioned above to get
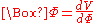
Working to first order of perturbation theory:
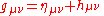
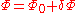
and after some tedious algebra, one can solve for the metric perturbation, which corresponds to the gravitational waves:
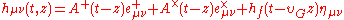
where
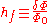
and
is the group velocityGroup velocity
The group velocity of a wave is the velocity with which the overall shape of the wave's amplitudes — known as the modulation or envelope of the wave — propagates through space....
of a wave packet
Wave packet
In physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...
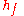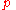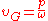centered in momentum as . The first two terms correspond to the usual from General Relativity gravitational waves while the third corresponds to the new massive polarization mode of 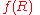theories, which moves at a speed (in units where 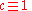.Equivalent formalism
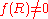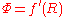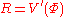We can simplify the analysis of f(R) theories by introducing an auxiliary field Φ. Assuming for all R, let V(Φ) be the Legendre transform of f(R) so that and . Then,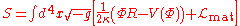We get the Euler-Lagrange equations
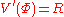
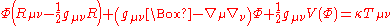
Eliminating Φ, we get exactly the same equations as before. However, the equations we do have are only second order in the derivatives, instead of fourth order.
We are currently working with the Jordan frame. By performing a conformal rescaling
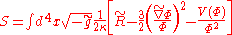
, we get to the Einstein frame.after integrating by parts.
Define
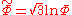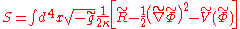
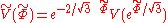
.This is none other an ordinary general relativity coupled to a real scalar field! Trying to use f(R) theories to describe the accelerating universe is practically equivalent to using quintessence
Quintessence (physics)
In physics, quintessence is a hypothetical form of dark energy postulated as an explanation of observations of an accelerating universe. It has been proposed by some physicists to be a fifth fundamental force...
.
Palatini f(R) Gravity
In Palatini f(R) gravity, one treats the metric and connection independently and varies the action with respect to each of them separately. Also important, one assumes the matter Lagrangian does not depend on the connection. These theories have been shown to be equivalent to Brans–Dicke theory with Due to the structure of the theory, however, Palatini f(R) theories appear to be in conflict with the Standard Model, may violate Solar system experiments, and seem to create unwanted singularities.Metric-Affine f(R) Gravity
In metric-affine f(R) gravity, one generalizes things even further, treating both the metric and connection independently, and assuming the matter Lagrangian depends on the connection as well.Tensorial generalization
f(R) gravity as presented in the previous sections is a scalar modification of general relativity. More generally, we can have a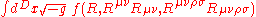coupling involving invariants of the Ricci tensor and the Weyl tensor
Weyl tensor
In differential geometry, the Weyl curvature tensor, named after Hermann Weyl, is a measure of the curvature of spacetime or, more generally, a pseudo-Riemannian manifold. Like the Riemann curvature tensor, the Weyl tensor expresses the tidal force that a body feels when moving along a geodesic...
. Special cases are f(R) gravity, conformal gravity, Gauss-Bonnet gravity and Lovelock gravity. It is suggested to consider dependency to the covariant derivative
Covariant derivative
In mathematics, the covariant derivative is a way of specifying a derivative along tangent vectors of a manifold. Alternatively, the covariant derivative is a way of introducing and working with a connection on a manifold by means of a differential operator, to be contrasted with the approach given...
of the Riemann tensor in order to resolve more problems. Notice that with any nontrivial tensorial dependence, we typically have additional massive spin-2 degrees of freedom, in addition to the massless graviton and a massive scalar. An exception is Gauss-Bonnet gravity where the fourth order terms for the spin-2 components cancel out.
Further reading
- A.A. Starobinsky, Phys. Lett. B, 91, 99 (1980), doi:10.1016/0370-2693(80)90670-X
- S.M. Carroll, V. Duvvuri, M. Trodden, and M.S. Turner, Phys. Rev. D 70, 043528 (2004), arXiv:astro-ph/0306438, June 2003: Is Cosmic Speed-Up Due to New Gravitational Physics?
- N.J. Poplawski, Phys. Rev. D 74, 084032 (2006), arXiv:gr-qc/0607124, Jul 2007: Interacting dark energy in f(R) gravity
- S. Capozziello, V.F. Cardone, A. Troisi, Feb 2006. 5pp. JCAP 0608:001,2006. [e-Print: astro-ph/0602349 Dark energy and dark matter as curvature effects.]
- S. Tsujikawa, arXiv:0705.1032, May 2007: Matter density perturbations and effective gravitational constant in modified gravity models of dark energy
- V. Faraoni, arXiv:0810.2602, Oct. 2008: f(R) gravity: successes and challenges
- E.E. Flanagan, arXiv:astro-ph/0308111, Aug. 2003: Palatini form of 1/R gravity
- S. Capozziello, Mauro Francaviglia, Gen.Rel.Grav.40:357 (2008) [ e-Print: arXiv:0706.1146 [astro-ph]Extended Theories of Gravity and their Cosmological and Astrophysical Applications]
- A. De Felice and S. Tsujikawa, "f(R) Theories", Living Rev. Relativity 13 (2010) 3, http://www.livingreviews.org/lrr-2010-3
- T.P. Sotiriou and V. Faraoni, arXiv:0805.1726, May 2008: f(R) theories of gravity
- T.P. Sotiriou, arXiv:0810.5594, Oct. 2008: 6+1 lessons from f(R) gravity
- S. Capozziello et al. ,Phys.Lett.B 669, 255 (2008) arXiv:0812.2272, Dec 2008: Massive gravitational waves from f(R) theories of gravity: Potential detection with LISA