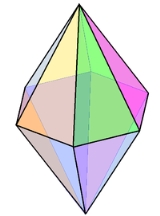
Face-uniform
Encyclopedia
In geometry
, a polytope
(a polyhedron
or a polychoron
for example) or tiling is isohedral or face-transitive when all its faces
are the same. More specifically, all faces must be not merely congruent
but must be transitive, i.e. must lie within the same symmetry orbit.
Isohedral polyhedra are called isohedra. They can be described by their face configuration
. A form that is isohedral and has regular vertices is also edge-transitive (isotoxal) and is said to be a quasiregular
dual
: some theorists regard these figures as truly quasiregular because they share the same symmetries, but this is not generally accepted.
A polyhedron which is isohedral has a dual polyhedron
that is vertex-transitive
(isogonal). The Catalan solids, the bipyramids and the trapezohedra are all isohedral. They are the duals of the isogonal Archimedean solids, prisms
and antiprisms, respectively. The Platonic solids, which are either self-dual or dual with another Platonic solid, are vertex, edge, and face-transitive (isogonal, isotoxal, and isohedral). A polyhedron which is isohedral and isogonal but not isotoxal is said to be noble
.
Convex isohedral polyhedra are the shapes that will make fair dice.
(n>3) or honeycomb
that has its cells
are congruent and transitive with each other.
A facet-transitive or isotopic figure is a n-dimensional polytopes or honeycomb, with its facets
((n-1)-face
s) congruent and transitive. The dual of an isotope is an isogonal polytope. By definition, this isotopic property is common to the duals of the uniform polytope
s.
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
(a polyhedron
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
or a polychoron
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
for example) or tiling is isohedral or face-transitive when all its faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
are the same. More specifically, all faces must be not merely congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
but must be transitive, i.e. must lie within the same symmetry orbit.
Isohedral polyhedra are called isohedra. They can be described by their face configuration
Face configuration
In geometry, a face configuration is notational description of a face-transitive polyhedron. It represents a sequential count of the number of faces that exist at each vertex around a face....
. A form that is isohedral and has regular vertices is also edge-transitive (isotoxal) and is said to be a quasiregular
Quasiregular polyhedron
In geometry, a quasiregular polyhedron is a semiregular polyhedron that has exactly two kinds of regular faces, which alternate around each vertex. They are edge-transitive and hence step closer to regularity than the semiregular which are merely vertex-transitive.There are only two convex...
dual
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
: some theorists regard these figures as truly quasiregular because they share the same symmetries, but this is not generally accepted.
A polyhedron which is isohedral has a dual polyhedron
Dual polyhedron
In geometry, polyhedra are associated into pairs called duals, where the vertices of one correspond to the faces of the other. The dual of the dual is the original polyhedron. The dual of a polyhedron with equivalent vertices is one with equivalent faces, and of one with equivalent edges is another...
that is vertex-transitive
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
(isogonal). The Catalan solids, the bipyramids and the trapezohedra are all isohedral. They are the duals of the isogonal Archimedean solids, prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
and antiprisms, respectively. The Platonic solids, which are either self-dual or dual with another Platonic solid, are vertex, edge, and face-transitive (isogonal, isotoxal, and isohedral). A polyhedron which is isohedral and isogonal but not isotoxal is said to be noble
Noble polyhedron
A noble polyhedron is one which is isohedral and isogonal . They were first studied in any depth by Hess and Bruckner around the turn of the century , and later by Grünbaum.-Classes of noble polyhedra:...
.
Convex isohedral polyhedra are the shapes that will make fair dice.
Examples
 The hexagonal bipyramid Hexagonal bipyramid A hexagonal bipyramid is a polyhedron formed from two hexagonal pyramids joined at their bases. The resulting solid has 12 triangular faces, 8 vertices and 18 edges. The 12 faces are identical isosceles triangles.It is one of an infinite set of bipyramids... , V4.4.6 is a nonregular Regular polyhedron A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags... example of an isohedral polyhedron. |
 The isohedral Cairo pentagonal tiling Cairo pentagonal tiling In geometry, the Cairo pentagonal tiling is a dual semiregular tiling of the Euclidean plane. It is given its name because it appears on the streets of Cairo and in many Islamic decorations. It is one of 14 known isohedral pentagon tilings.... , V3.3.4.3.4 |
 The rhombic dodecahedral honeycomb Rhombic dodecahedral honeycomb The rhombic dodecahedra honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which is believed to be the densest possible packing of equal spheres in ordinary space .It consists of copies of a single cell, the rhombic... is an example of an isohedral space-filling honeycomb. |
Related terms
A cell-transitive or isochoric figure is an n-polytopePolytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
(n>3) or honeycomb
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
that has its cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
are congruent and transitive with each other.
A facet-transitive or isotopic figure is a n-dimensional polytopes or honeycomb, with its facets
Facet (mathematics)
A facet of a simplicial complex is a maximal simplex.In the general theory of polyhedra and polytopes, two conflicting meanings are currently jostling for acceptability:...
((n-1)-face
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
s) congruent and transitive. The dual of an isotope is an isogonal polytope. By definition, this isotopic property is common to the duals of the uniform polytope
Uniform polytope
A uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....
s.
- An isotopic 2-dimensional figure is isotoxal (edge-transitive).
- An isotopic 3-dimensional figure is isohedral (face-transitive).
- An isotopic 4-dimensional figure is isochoric (cell-transitive).

