Frame-dragging
Encyclopedia
Einstein's general theory of relativity predicts that non-static, stationary mass-energy distributions affect spacetime
in a peculiar way giving rise to a phenomenon usually known as frame-dragging. The first frame-dragging effect was derived in 1918, in the framework of general relativity, by the Austrian physicists Josef Lense
and Hans Thirring
, and is also known as the Lense–Thirring effect. They predicted that the rotation of a massive object would distort spacetime metric
, making the orbit of a nearby test particle precess. This does not happen in Newtonian mechanics for which the gravitational field
of a body depends only on its mass, not on its rotation. The Lense-Thirring effect is very small—about one part in a few trillion. To detect it, it is necessary to examine a very massive object, or build an instrument that is very sensitive. More generally, the subject of effects caused by mass-energy currents is known as gravitomagnetism
, in analogy with classical electromagnetism
.
experiment. Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction.
Also, an inner region is dragged more than an outer region. This produces interesting locally-rotating frames. For example, imagine that an "ice skater", in orbit over the equator of a black hole and rotationally at rest with respect to the stars, extends her arms. The arm extended toward the black hole will be torqued spinward. The arm extended away from the black hole will be torqued anti-spinward. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This is the opposite of what happens in everyday experience. If she is already rotating at some speed when she extends her arms, inertial effects and frame-dragging effects will balance and her spin will not change. Due to the Principle of Equivalence
gravitational effects are locally indistinguishable from inertial effects, so the rotation rate at which, when she extends her arms, nothing happens is her local reference for non-rotation. This frame is rotating with respect to the fixed stars and counter-rotating with respect to the black hole. A useful metaphor is a planetary gear system with the black hole being the sun gear, the ice skater being a planetary gear and the outside universe being the ring gear. See Mach's principle
.
Another interesting consequence is that, for an object constrained in an equatorial orbit, but not in freefall, it weighs more if orbiting anti-spinward, and less if orbiting spinward. For example, in a suspended equatorial bowling alley, a bowling ball rolled anti-spinward would weigh more than the same ball rolled in a spinward direction. Note, frame dragging will neither accelerate or slow down the bowling ball in either direction. It is not a "viscosity". Similarly, a stationary plumb-bob
suspended over the rotating object will not list. It will hang vertically. If it starts to fall, induction will push it in the spinward direction.
Linear frame dragging is the similarly inevitable result of the general principle of relativity, applied to linear momentum. Although it arguably has equal theoretical legitimacy to the "rotational" effect, the difficulty of obtaining an experimental verification of the effect means that it receives much less discussion and is often omitted from articles on frame-dragging (but see Einstein, 1921).
Static mass increase is a third effect noted by Einstein in the same paper. The effect is an increase in inertia
of a body when other masses are placed nearby. While not strictly a frame dragging effect (the term frame dragging is not used by Einstein), it is demonstrated by Einstein that it derives from the same equation of general relativity. It is also a tiny effect that is difficult to confirm experimentally.
satellite, launched in 1976, apart from the orbital planes which should have been displaced by 180 deg apart: the so-called butterfly configuration. The measurable quantity was, in this case, the sum of the nodes of LAGEOS and of the new spacecraft, later named LAGEOS III, LARES, WEBER-SAT. Although extensively studied by various groups, such an idea has not yet been implemented. The butterfly configuration would allow, in principle, to measure not only the sum of the nodes but also the difference of the perigees, although such Keplerian orbital elements are more affected by the non-gravitational perturbations like the direct solar radiation pressure: the use of the active, drag-free technology would be required. Other proposed approaches involved the use of a single satellite to be placed in near polar orbit of low altitude, but such a strategy has been shown to be unfeasible. In order to enhance the possibilities of being implemented, it has been recently claimed that LARES/WEBER-SAT would be able to measure the effects induced by the multidimensional braneworld model
by Dvali, Gabadaze and Porrati and to improve by two orders of magnitude the present-day level of accuracy of the equivalence principle. Such claims have been shown to be highly unrealistic.
) technique to measure the Lense–Thirring effect dates back to 1977–1978. Tests have started to be effectively performed by using the LAGEOS
and LAGEOS II satellites in 1996, according to a strategy involving the use of a suitable combination of the nodes of both satellites and the perigee of LAGEOS II. The latest tests with the LAGEOS
satellites have been performed in 2004-2006 by discarding the perigee of LAGEOS II and using a linear combination involving only the nodes of both the spacecraft.
Although the predictions of general relativity are compatible with the experimental results, the realistic evaluation of the total error raised a debate.
Another test of the Lense–Thirring effect in the gravitational field of Mars, performed by suitably interpreting the data of the Mars Global Surveyor
(MGS) spacecraft, has been recently reported. There is also debate about this test. Attempts to detect the Lense–Thirring effect induced by the Sun's rotation on the orbits of the inner planets of the Solar System have been reported as well: the predictions of general relativity are compatible with the estimated corrections to the perihelia precessions, although the errors are still large. However, the inclusion of the radiometric data from the Magellan orbiter recently allowed Pitjeva
to greatly improve the determination of the unmodelled precession of the perihelion of Venus. It amounts to −0.0004 ± 0.0001 arcseconds/century, while the Lense–Thirring effect for the Venus' perihelion is just -0.0003 arcseconds/century. The system of the Galilean satellites of Jupiter was investigated as well, following the original suggestion by Lense and Thirring.
Recently, an indirect test of the gravitomagnetic interaction accurate to 0.1% has been reported by Murphy et al. with the Lunar laser ranging (LLR) technique, but Kopeikin questioned the ability of LLR to be sensitive to gravitomagnetism.
The Gravity Probe B
experiment was a satellite-based mission by a Stanford group and NASA, used to experimentally measure another gravitomagnetic effect, the Schiff precession of a gyroscope, to an expected 1% accuracy or better. Unfortunately such accuracy was not achieved. The first preliminary results released in April 2007 pointed towards an accuracy of 256–128%, with the hope of reaching about 13% in December 2007.
In 2008 the Senior Review Report of the NASA Astrophysics Division Operating Missions stated that it was unlikely that Gravity Probe B team will be able to reduce the errors to the level necessary to produce a convincing test of currently-untested aspects of General Relativity (including Frame-dragging).
On May 4, 2011, the Stanford-based analysis group and NASA announced the final report, and in it the data from GP-B demonstrated the frame-dragging effect with an error of about 19 percent. The findings were accepted for publication in the journal Physical Review Letters
.
(ASI) has announced that the LARES
satellite should be launched with a Vega rocket at the beginning of 2011. The goal of LARES is to measure the Lense–Thirring effect to 1%, but there are doubts that this can be achieved, mainly due to the relatively low orbit which LARES should be inserted into bringing into play more mismodelled even zonal harmonics. That is, spherical harmonics
of the Earth's gravitational field caused by mass concentrations (like mountains) can drag a satellite in a way which may be difficult to distinguish from frame-dragging.
In the case of stars orbiting close to a spinning, supermassive black hole, frame dragging should cause the star's orbital plane to precess about the black hole spin axis. This effect should be detectable within the next few years via astrometric
monitoring of stars at the center of the Milky Way
galaxy.
By comparing the rate of orbital precession of two stars on different orbits, it is possible in principle to test the no-hair theorems of general relativity, in addition to measuring the spin of the black hole.
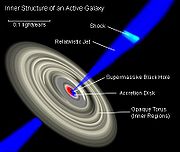Relativistic jet
s may provide evidence for the reality of frame-dragging. Gravitomagnetic forces produced by the Lense–Thirring effect (frame dragging) within the ergosphere
of rotating black hole
s combined with the energy extraction mechanism by Penrose
have been used to explain the observed properties of relativistic jet
s. The gravitomagnetic model developed by Reva Kay Williams predicts the observed high energy particles (~GeV) emitted by quasars and active galactic nuclei; the extraction of X-rays, γ-rays, and relativistic e-e+ pairs; the collimated jets about the polar axis; and the asymmetrical formation of jets (relative to the orbital plane).
, which describes the geometry of spacetime
in the vicinity of a mass M rotating with angular momentum
J
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in a peculiar way giving rise to a phenomenon usually known as frame-dragging. The first frame-dragging effect was derived in 1918, in the framework of general relativity, by the Austrian physicists Josef Lense
Josef Lense
Josef Lense was an Austrian physicistIn 1914 Lense got his doctorate under Samuel Oppenheim. From 1927-28 he was Professor ordinarius and from 1928-1946 Professor extraordinarius for applied mathematics at the Technical University of Munich...
and Hans Thirring
Hans Thirring
Hans Thirring was an Austrian theoretical physicist, professor, and father of the physicist Walter Thirring....
, and is also known as the Lense–Thirring effect. They predicted that the rotation of a massive object would distort spacetime metric
Metric tensor (general relativity)
In general relativity, the metric tensor is the fundamental object of study. It may loosely be thought of as a generalization of the gravitational field familiar from Newtonian gravitation...
, making the orbit of a nearby test particle precess. This does not happen in Newtonian mechanics for which the gravitational field
Gravitational field
The gravitational field is a model used in physics to explain the existence of gravity. In its original concept, gravity was a force between point masses...
of a body depends only on its mass, not on its rotation. The Lense-Thirring effect is very small—about one part in a few trillion. To detect it, it is necessary to examine a very massive object, or build an instrument that is very sensitive. More generally, the subject of effects caused by mass-energy currents is known as gravitomagnetism
Gravitomagnetism
Gravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
, in analogy with classical electromagnetism
Classical electromagnetism
Classical electromagnetism is a branch of theoretical physics that studies consequences of the electromagnetic forces between electric charges and currents...
.
Frame dragging effects
Rotational frame-dragging (the Lense–Thirring effect) appears in the general principle of relativity and similar theories in the vicinity of rotating massive objects. Under the Lense–Thirring effect, the frame of reference in which a clock ticks the fastest is one which is revolving around the object as viewed by a distant observer. This also means that light traveling in the direction of rotation of the object will move past the massive object faster than light moving against the rotation, as seen by a distant observer. It is now the best-known effect, partly thanks to the Gravity Probe BGravity Probe B
Gravity Probe B is a satellite-based mission which launched on 20 April 2004 on a Delta II rocket. The spaceflight phase lasted until 2005; its aim was to measure spacetime curvature near Earth, and thereby the stress–energy tensor in and near Earth...
experiment. Qualitatively, frame-dragging can be viewed as the gravitational analog of electromagnetic induction.
Also, an inner region is dragged more than an outer region. This produces interesting locally-rotating frames. For example, imagine that an "ice skater", in orbit over the equator of a black hole and rotationally at rest with respect to the stars, extends her arms. The arm extended toward the black hole will be torqued spinward. The arm extended away from the black hole will be torqued anti-spinward. She will therefore be rotationally sped up, in a counter-rotating sense to the black hole. This is the opposite of what happens in everyday experience. If she is already rotating at some speed when she extends her arms, inertial effects and frame-dragging effects will balance and her spin will not change. Due to the Principle of Equivalence
Equivalence principle
In the physics of general relativity, the equivalence principle is any of several related concepts dealing with the equivalence of gravitational and inertial mass, and to Albert Einstein's assertion that the gravitational "force" as experienced locally while standing on a massive body is actually...
gravitational effects are locally indistinguishable from inertial effects, so the rotation rate at which, when she extends her arms, nothing happens is her local reference for non-rotation. This frame is rotating with respect to the fixed stars and counter-rotating with respect to the black hole. A useful metaphor is a planetary gear system with the black hole being the sun gear, the ice skater being a planetary gear and the outside universe being the ring gear. See Mach's principle
Mach's principle
In theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
.
Another interesting consequence is that, for an object constrained in an equatorial orbit, but not in freefall, it weighs more if orbiting anti-spinward, and less if orbiting spinward. For example, in a suspended equatorial bowling alley, a bowling ball rolled anti-spinward would weigh more than the same ball rolled in a spinward direction. Note, frame dragging will neither accelerate or slow down the bowling ball in either direction. It is not a "viscosity". Similarly, a stationary plumb-bob
Plumb-bob
A plumb-bob or a plummet is a weight, usually with a pointed tip on the bottom, that is suspended from a string and used as a vertical reference line, or plumb-line....
suspended over the rotating object will not list. It will hang vertically. If it starts to fall, induction will push it in the spinward direction.
Linear frame dragging is the similarly inevitable result of the general principle of relativity, applied to linear momentum. Although it arguably has equal theoretical legitimacy to the "rotational" effect, the difficulty of obtaining an experimental verification of the effect means that it receives much less discussion and is often omitted from articles on frame-dragging (but see Einstein, 1921).
Static mass increase is a third effect noted by Einstein in the same paper. The effect is an increase in inertia
Inertia
Inertia is the resistance of any physical object to a change in its state of motion or rest, or the tendency of an object to resist any change in its motion. It is proportional to an object's mass. The principle of inertia is one of the fundamental principles of classical physics which are used to...
of a body when other masses are placed nearby. While not strictly a frame dragging effect (the term frame dragging is not used by Einstein), it is demonstrated by Einstein that it derives from the same equation of general relativity. It is also a tiny effect that is difficult to confirm experimentally.
Proposals
In 1976 Van Patten and Everitt proposed to implement a dedicated mission aimed to measure the Lense–Thirring node precession of a pair of counter-orbiting spacecraft to be placed in terrestrial polar orbits with drag-free apparatus. A somewhat equivalent, cheaper version of such an idea was put forth in 1986 by Ciufolini who proposed to launch a passive, geodetic satellite in an orbit identical to that of the LAGEOSLAGEOS
LAGEOS, or Laser Geodynamics Satellites, are a series of scientific research satellites designed to provide an orbiting laser ranging benchmark for geodynamical studies of the Earth...
satellite, launched in 1976, apart from the orbital planes which should have been displaced by 180 deg apart: the so-called butterfly configuration. The measurable quantity was, in this case, the sum of the nodes of LAGEOS and of the new spacecraft, later named LAGEOS III, LARES, WEBER-SAT. Although extensively studied by various groups, such an idea has not yet been implemented. The butterfly configuration would allow, in principle, to measure not only the sum of the nodes but also the difference of the perigees, although such Keplerian orbital elements are more affected by the non-gravitational perturbations like the direct solar radiation pressure: the use of the active, drag-free technology would be required. Other proposed approaches involved the use of a single satellite to be placed in near polar orbit of low altitude, but such a strategy has been shown to be unfeasible. In order to enhance the possibilities of being implemented, it has been recently claimed that LARES/WEBER-SAT would be able to measure the effects induced by the multidimensional braneworld model
DGP model
The DGP model is a model of gravity proposed by Gia Dvali, Gregory Gabadadze, and Massimo Porrati in 2000. The model is popular among some model builders, but has resisted being embedded into string theory....
by Dvali, Gabadaze and Porrati and to improve by two orders of magnitude the present-day level of accuracy of the equivalence principle. Such claims have been shown to be highly unrealistic.
Analysis of experimental data
Limiting the scope to the scenarios involving existing orbiting bodies, the first proposal to use the LAGEOS satellite and the Satellite Laser Ranging (SLRSatellite laser ranging
In satellite laser ranging a global network of observation stations measure the round trip time of flight of ultrashort pulses of light to satellites equipped with retroreflectors...
) technique to measure the Lense–Thirring effect dates back to 1977–1978. Tests have started to be effectively performed by using the LAGEOS
LAGEOS
LAGEOS, or Laser Geodynamics Satellites, are a series of scientific research satellites designed to provide an orbiting laser ranging benchmark for geodynamical studies of the Earth...
and LAGEOS II satellites in 1996, according to a strategy involving the use of a suitable combination of the nodes of both satellites and the perigee of LAGEOS II. The latest tests with the LAGEOS
LAGEOS
LAGEOS, or Laser Geodynamics Satellites, are a series of scientific research satellites designed to provide an orbiting laser ranging benchmark for geodynamical studies of the Earth...
satellites have been performed in 2004-2006 by discarding the perigee of LAGEOS II and using a linear combination involving only the nodes of both the spacecraft.
Although the predictions of general relativity are compatible with the experimental results, the realistic evaluation of the total error raised a debate.
Another test of the Lense–Thirring effect in the gravitational field of Mars, performed by suitably interpreting the data of the Mars Global Surveyor
Mars Global Surveyor
The Mars Global Surveyor was a US spacecraft developed by NASA's Jet Propulsion Laboratory and launched November 1996. It began the United States's return to Mars after a 10-year absence. It completed its primary mission in January 2001 and was in its third extended mission phase when, on 2...
(MGS) spacecraft, has been recently reported. There is also debate about this test. Attempts to detect the Lense–Thirring effect induced by the Sun's rotation on the orbits of the inner planets of the Solar System have been reported as well: the predictions of general relativity are compatible with the estimated corrections to the perihelia precessions, although the errors are still large. However, the inclusion of the radiometric data from the Magellan orbiter recently allowed Pitjeva
Elena V. Pitjeva
Elena Vladimirovna Pitjeva is a Russian astronomer working at the Institute of Applied Astronomy, Russian Academy of Sciences, St. Petersburg. She has published over 100 articles, as listed in Google Scholar and the Astrophysics Data System in the field of solar system dynamics and celestial...
to greatly improve the determination of the unmodelled precession of the perihelion of Venus. It amounts to −0.0004 ± 0.0001 arcseconds/century, while the Lense–Thirring effect for the Venus' perihelion is just -0.0003 arcseconds/century. The system of the Galilean satellites of Jupiter was investigated as well, following the original suggestion by Lense and Thirring.
Recently, an indirect test of the gravitomagnetic interaction accurate to 0.1% has been reported by Murphy et al. with the Lunar laser ranging (LLR) technique, but Kopeikin questioned the ability of LLR to be sensitive to gravitomagnetism.
The Gravity Probe B
Gravity Probe B
Gravity Probe B is a satellite-based mission which launched on 20 April 2004 on a Delta II rocket. The spaceflight phase lasted until 2005; its aim was to measure spacetime curvature near Earth, and thereby the stress–energy tensor in and near Earth...
experiment was a satellite-based mission by a Stanford group and NASA, used to experimentally measure another gravitomagnetic effect, the Schiff precession of a gyroscope, to an expected 1% accuracy or better. Unfortunately such accuracy was not achieved. The first preliminary results released in April 2007 pointed towards an accuracy of 256–128%, with the hope of reaching about 13% in December 2007.
In 2008 the Senior Review Report of the NASA Astrophysics Division Operating Missions stated that it was unlikely that Gravity Probe B team will be able to reduce the errors to the level necessary to produce a convincing test of currently-untested aspects of General Relativity (including Frame-dragging).
On May 4, 2011, the Stanford-based analysis group and NASA announced the final report, and in it the data from GP-B demonstrated the frame-dragging effect with an error of about 19 percent. The findings were accepted for publication in the journal Physical Review Letters
Physical Review Letters
Physical Review Letters , established in 1958, is a peer reviewed, scientific journal that is published 52 times per year by the American Physical Society...
.
Possible future tests
A 1% measurement of the Lense–Thirring effect in the gravitational field of the Earth could be obtained by launching at least two entirely new satellites, preferably with active mechanisms of compensation of the non-gravitational forces, in eccentric orbits, as stated in 2005 by Lorenzo Iorio. Recently, the Italian Space AgencyItalian Space Agency
The Italian Space Agency is a government agency established in 1988 to fund, regulate and coordinate space exploration activities in Italy...
(ASI) has announced that the LARES
LARES (satellite)
LARES is an Italian Space Agency scientific satellite to be launched with the new European launch vehicle Vega.LARES will be launched by Vega's maiden flight, scheduled for 2011.- The mission :...
satellite should be launched with a Vega rocket at the beginning of 2011. The goal of LARES is to measure the Lense–Thirring effect to 1%, but there are doubts that this can be achieved, mainly due to the relatively low orbit which LARES should be inserted into bringing into play more mismodelled even zonal harmonics. That is, spherical harmonics
Spherical harmonics
In mathematics, spherical harmonics are the angular portion of a set of solutions to Laplace's equation. Represented in a system of spherical coordinates, Laplace's spherical harmonics Y_\ell^m are a specific set of spherical harmonics that forms an orthogonal system, first introduced by Pierre...
of the Earth's gravitational field caused by mass concentrations (like mountains) can drag a satellite in a way which may be difficult to distinguish from frame-dragging.
In the case of stars orbiting close to a spinning, supermassive black hole, frame dragging should cause the star's orbital plane to precess about the black hole spin axis. This effect should be detectable within the next few years via astrometric
Astrometry
Astrometry is the branch of astronomy that involves precise measurements of the positions and movements of stars and other celestial bodies. The information obtained by astrometric measurements provides information on the kinematics and physical origin of our Solar System and our Galaxy, the Milky...
monitoring of stars at the center of the Milky Way
Milky Way
The Milky Way is the galaxy that contains the Solar System. This name derives from its appearance as a dim un-resolved "milky" glowing band arching across the night sky...
galaxy.
By comparing the rate of orbital precession of two stars on different orbits, it is possible in principle to test the no-hair theorems of general relativity, in addition to measuring the spin of the black hole.
Astronomical evidence
Relativistic jet
Relativistic jets are extremely powerful jets of plasma which emerge from presumed massive objects at the centers of some active galaxies, notably radio galaxies and quasars. Their lengths can reach several thousand or even hundreds of thousands of light years...
s may provide evidence for the reality of frame-dragging. Gravitomagnetic forces produced by the Lense–Thirring effect (frame dragging) within the ergosphere
Ergosphere
The ergosphere is a region located outside a rotating black hole. Its name is derived from the Greek word ergon, which means “work”. It received this name because it is theoretically possible to extract energy and mass from the black hole in this region...
of rotating black hole
Rotating black hole
A rotating black hole is a black hole that possesses spin angular momentum.-Types of black holes:There are four known, exact, black hole solutions to Einstein's equations, which describe gravity in General Relativity. Two of these rotate...
s combined with the energy extraction mechanism by Penrose
Roger Penrose
Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...
have been used to explain the observed properties of relativistic jet
Relativistic jet
Relativistic jets are extremely powerful jets of plasma which emerge from presumed massive objects at the centers of some active galaxies, notably radio galaxies and quasars. Their lengths can reach several thousand or even hundreds of thousands of light years...
s. The gravitomagnetic model developed by Reva Kay Williams predicts the observed high energy particles (~GeV) emitted by quasars and active galactic nuclei; the extraction of X-rays, γ-rays, and relativistic e-e+ pairs; the collimated jets about the polar axis; and the asymmetrical formation of jets (relative to the orbital plane).
Mathematical derivation of frame-dragging
Frame-dragging may be illustrated most readily using the Kerr metricKerr metric
The Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
, which describes the geometry of spacetime
Spacetime
In physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
in the vicinity of a mass M rotating with angular momentum
Angular momentum
In physics, angular momentum, moment of momentum, or rotational momentum is a conserved vector quantity that can be used to describe the overall state of a physical system...
J
-
-
-
where rs is the Schwarzschild radiusSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
and where the following shorthand variables have been introduced for brevity
In the non-relativistic limit where M (or, equivalently, rs) goes to zero, the Kerr metric becomes the orthogonal metric for the oblate spheroidal coordinatesOblate spheroidal coordinatesOblate spheroidal coordinates are a three-dimensional orthogonal coordinate system that results from rotating the two-dimensional elliptic coordinate system about the non-focal axis of the ellipse, i.e., the symmetry axis that separates the foci. Thus, the two foci are transformed into a ring of...
We may re-write the Kerr metric in the following form
This metric is equivalent to a co-rotating reference frame that is rotating with angular speed Ω that depends on both the radius r and the colatitudeColatitudeIn spherical coordinates, colatitude is the complementary angle of the latitude, i.e. the difference between 90° and the latitude.-Astronomical use:The colatitude is useful in astronomy because it refers to the zenith distance of the celestial poles...
θ
In the plane of the equator this simplifies to:
Thus, an inertial reference frame is entrained by the rotating central mass to participate in the latter's rotation; this is frame-dragging.
An extreme version of frame dragging occurs within the ergosphere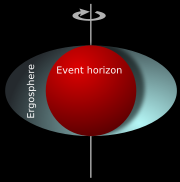
ErgosphereThe ergosphere is a region located outside a rotating black hole. Its name is derived from the Greek word ergon, which means “work”. It received this name because it is theoretically possible to extract energy and mass from the black hole in this region...
of a rotating black holeBlack holeA black hole is a region of spacetime from which nothing, not even light, can escape. The theory of general relativity predicts that a sufficiently compact mass will deform spacetime to form a black hole. Around a black hole there is a mathematically defined surface called an event horizon that...
. The Kerr metric has two surfaces on which it appears to be singular. The inner surface corresponds to a spherical event horizonEvent horizonIn general relativity, an event horizon is a boundary in spacetime beyond which events cannot affect an outside observer. In layman's terms it is defined as "the point of no return" i.e. the point at which the gravitational pull becomes so great as to make escape impossible. The most common case...
similar to that observed in the Schwarzschild metricSchwarzschild metricIn Einstein's theory of general relativity, the Schwarzschild solution describes the gravitational field outside a spherical, uncharged, non-rotating mass such as a star, planet, or black hole. It is also a good approximation to the gravitational field of a slowly rotating body like the Earth or...
; this occurs at
where the purely radial component grr of the metric goes to infinity. The outer surface is not a sphere, but an oblate spheroid that touches the inner surface at the poles of the rotation axis, where the colatitude θ equals 0 or π; its radius is defined by the formula
where the purely temporal component gtt of the metric changes sign from positive to negative. The space between these two surfaces is called the ergosphereErgosphereThe ergosphere is a region located outside a rotating black hole. Its name is derived from the Greek word ergon, which means “work”. It received this name because it is theoretically possible to extract energy and mass from the black hole in this region...
. A moving particle experiences a positive proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
along its worldline, its path through spacetimeSpacetimeIn physics, spacetime is any mathematical model that combines space and time into a single continuum. Spacetime is usually interpreted with space as being three-dimensional and time playing the role of a fourth dimension that is of a different sort from the spatial dimensions...
. However, this is impossible within the ergosphere, where gtt is negative, unless the particle is co-rotating with the interior mass M with an angular speed at least of Ω. However, as seen above, frame-dragging occurs about every rotating mass and at every radius r and colatitude θ, not only within the ergosphere.
Lense–Thirring effect inside a rotating shell
Inside a rotating spherical shell the acceleration due to the Lense–Thirring effect would be
-
where the coefficients are
-
-
for MG ≪ Rc2 or more precisely,
-
The space-time inside the rotating spherical shell will not be flat. A flat space-time inside a rotating mass shell is possible if the shell is allowed to deviate from a precisely spherical shape and the mass density inside the shell is allowed to vary.
See also
- Kerr metricKerr metricThe Kerr metric describes the geometry of empty spacetime around an uncharged axially-symmetric black-hole with an event horizon which is topologically a sphere. The Kerr metric is an exact solution of the Einstein field equations of general relativity; these equations are highly non-linear, which...
- Geodetic effectGeodetic effectThe geodetic effect represents the effect of the curvature of spacetime, predicted by general relativity, on a vector carried along with an orbiting body...
- GravitomagnetismGravitomagnetismGravitomagnetism , refers to a set of formal analogies between Maxwell's field equations and an approximation, valid under certain conditions, to the Einstein field equations for general relativity. The most common version of GEM is valid only far from isolated sources, and for slowly moving test...
- Mach's principleMach's principleIn theoretical physics, particularly in discussions of gravitation theories, Mach's principle is the name given by Einstein to an imprecise hypothesis often credited to the physicist and philosopher Ernst Mach....
- Broad iron K lineBroad Iron K lineIn astronomy, the broad iron K line is a spectral line that is an accurate measure of a black hole's immense gravitational force. The name refers to the shape, on a spectrogram, of light emitted by iron atoms near the black hole surface...
- Relativistic jetRelativistic jetRelativistic jets are extremely powerful jets of plasma which emerge from presumed massive objects at the centers of some active galaxies, notably radio galaxies and quasars. Their lengths can reach several thousand or even hundreds of thousands of light years...
- Lense–Thirring precession
External links
- NASA RELEASE: 04-351 As The World Turns, It Drags Space And Time
- New Scientist press release of the MGS test by Iorio in the gravitational field of Mars
- Paper by Giampiero Sindoni, Claudio Paris and Paolo Ialongo about the Mars-MGS test (unpublished)
- Paper by G. Felici about the Mars-MGS test (unpublished)
- Paper by Kris Krogh about the Mars-MGS test
- Reply by Ignazio Ciufolini and Erricos Pavlis about some criticisms by Iorio
- Frame dragging applied to relativistic jets
- Frame Dragging
- Duke University press release: General Relativistic Frame Dragging
- MSNBC report on X-ray observations
- Ciufolini et al. LAGEOS paper 1997 - 25% error
- Ciufolini update Sep 2002 - 20% error
- Press release regarding LAGEOS study
- Preprint by Ries et al.
- Ciufolini and Pavlis Nature new article on 2004 re-analysis of the LAGEOS data
- Iorio New Astronomy general paper with full references
- Iorio J. of Geodesy paper on the impact of the secular variations of the even zonal harmonics of the geopotential
- Iorio Planetary Space Science paper
- Iorio General Relativity and Gravitation paper on LARES
- Iorio Advances in Space Research paper on LARES
- An Assessment of the Systematic Uncertainty in Present and Future Tests of the Lense–Thirring Effect with Satellite Laser Ranging IorioSpace Science Reviews paper on LARES
- Advances in the measurement of the Lense–Thirring effect with Satellite Laser Ranging in the gravitational field of the Earth Iorio invited book chapter on LARES
An early version of this article was adapted from public domain material from http://science.msfc.nasa.gov/newhome/headlines/ast06nov97_1.htm - Kerr metric
-
-
-
-
-
-