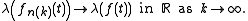Franková-Helly selection theorem
Encyclopedia
In mathematics
, the Fraňková–Helly selection theorem is a generalisation of Helly's selection theorem
for functions of bounded variation
to the case of regulated function
s. It was proved in 1991 by the Czech
mathematician
Dana Fraňková.
, and let BV([0, T]; X) denote the normed vector space
of all functions f : [0, T] → X with finite total variation over the interval
[0, T], equipped with the total variation norm. It is well-known that BV([0, T]; X) satisfies the compactness theorem
known as Helly's selection theorem: given any sequence of functions (fn)n∈N in BV([0, T]; X) that is uniformly bounded in the total variation norm, there exists a subsequence
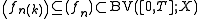
and a limit function f ∈ BV([0, T]; X) such that fn(k)(t) converges weakly
in X to f(t) for every t ∈ [0, T]. That is, for every continuous linear functional λ ∈ X*,
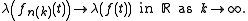
Consider now the Banach space
Reg([0, T]; X) of all regulated functions f : [0, T] → X, equipped with the supremum norm. Helly's theorem does not hold for the space Reg([0, T]; X): a counterexample
is given by the sequence
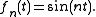
One may ask, however, if a weaker selection theorem is true, and the Fraňková–Helly selection theorem is such a result.
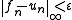
and

where |-| denotes the norm
in X and Var(u) denotes the variation of u, which is defined to be the supremum
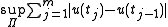
over all partitions
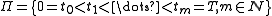
of [0, T]. Then there exists a subsequence
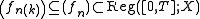
and a limit function f ∈ Reg([0, T]; X) such that fn(k)(t) converges weakly in X to f(t) for every t ∈ [0, T]. That is, for every continuous linear functional λ ∈ X*,
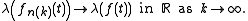
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Fraňková–Helly selection theorem is a generalisation of Helly's selection theorem
Helly's selection theorem
In mathematics, Helly's selection theorem states that a sequence of functions that is locally of bounded total variation and uniformly bounded at a point has a convergent subsequence. In other words, it is a compactness theorem for the space BVloc. It is named for the Austrian mathematician Eduard...
for functions of bounded variation
Bounded variation
In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
to the case of regulated function
Regulated function
In mathematics, a regulated function is a "well-behaved" function of a single real variable. Regulated functions arise as a class of integrable functions, and have several equivalent characterisations...
s. It was proved in 1991 by the Czech
Czech Republic
The Czech Republic is a landlocked country in Central Europe. The country is bordered by Poland to the northeast, Slovakia to the east, Austria to the south, and Germany to the west and northwest....
mathematician
Mathematician
A mathematician is a person whose primary area of study is the field of mathematics. Mathematicians are concerned with quantity, structure, space, and change....
Dana Fraňková.
Background
Let X be a separable Hilbert spaceHilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and let BV([0, T]; X) denote the normed vector space
Normed vector space
In mathematics, with 2- or 3-dimensional vectors with real-valued entries, the idea of the "length" of a vector is intuitive and can easily be extended to any real vector space Rn. The following properties of "vector length" are crucial....
of all functions f : [0, T] → X with finite total variation over the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[0, T], equipped with the total variation norm. It is well-known that BV([0, T]; X) satisfies the compactness theorem
Compact space
In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
known as Helly's selection theorem: given any sequence of functions (fn)n∈N in BV([0, T]; X) that is uniformly bounded in the total variation norm, there exists a subsequence
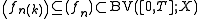
and a limit function f ∈ BV([0, T]; X) such that fn(k)(t) converges weakly
Weak convergence
In mathematics, weak convergence may refer to:* The weak convergence of random variables of a probability distribution.* The weak convergence of a sequence of probability measures....
in X to f(t) for every t ∈ [0, T]. That is, for every continuous linear functional λ ∈ X*,
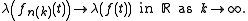
Consider now the Banach space
Banach space
In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
Reg([0, T]; X) of all regulated functions f : [0, T] → X, equipped with the supremum norm. Helly's theorem does not hold for the space Reg([0, T]; X): a counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
is given by the sequence
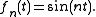
One may ask, however, if a weaker selection theorem is true, and the Fraňková–Helly selection theorem is such a result.
Statement of the Fraňková–Helly selection theorem
As before, let X be a separable Hilbert space and let Reg([0, T]; X) denote the space of regulated functions f : [0, T] → X, equipped with the supremum norm. Let (fn)n∈N be a sequence in Reg([0, T]; X) satisfying the following condition: for every ε > 0, there exists some Lε > 0 so that each fn may be approximated by a un ∈ BV([0, T]; X) satisfying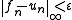
and

where |-| denotes the norm
Norm (mathematics)
In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
in X and Var(u) denotes the variation of u, which is defined to be the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
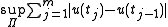
over all partitions
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
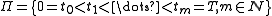
of [0, T]. Then there exists a subsequence
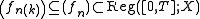
and a limit function f ∈ Reg([0, T]; X) such that fn(k)(t) converges weakly in X to f(t) for every t ∈ [0, T]. That is, for every continuous linear functional λ ∈ X*,