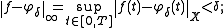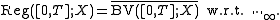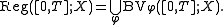In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a regulated function (or ruled function) is a "well-behaved" function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 of a single real

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

 variable. Regulated functions arise as a class of integrable functions, and have several equivalent characterisations. Regulated functions were introduced by Georg Aumann in 1954; the corresponding regulated integral

Regulated integral

In mathematics, the regulated integral is a definition of integration for regulated functions, which are defined to be uniform limits of step functions. The use of the regulated integral instead of the Riemann integral has been advocated by Nicolas Bourbaki and Jean Dieudonné.-Definition on step...

 was promoted by the Bourbaki group, including Jean Dieudonné

Jean Dieudonné

Jean Alexandre Eugène Dieudonné was a French mathematician, notable for research in abstract algebra and functional analysis, for close involvement with the Nicolas Bourbaki pseudonymous group and the Éléments de géométrie algébrique project of Alexander Grothendieck, and as a historian of...

.

Definition

Let X be a Banach space

Banach space

In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...

 with norm || - ||_X. A function f : [0, T] → X is said to be a regulated function if one (and hence both) of the following two equivalent conditions holds true :

• for every t in the interval
  Interval (mathematics)
  In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
  
   [0, T], both the left and right limits
  Limit of a function
  In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
  
   f(t−) and f(t+) exist in X (apart from, obviously, f(0−) and f(T+));

• there exists a sequence of step function
  Step function
  In mathematics, a function on the real numbers is called a step function if it can be written as a finite linear combination of indicator functions of intervals...
  
  s φ_n : [0, T] → X converging uniformly to f (i.e. with respect to the supremum norm || - ||_∞).

It requires a little work to show that these two conditions are equivalent. However, it is relatively easy to see that the second condition may be re-stated in the following equivalent ways:

• for every δ > 0, there is some step function φ_δ : [0, T] → X such that

• f lies in the closure
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
   of the space Step([0, T]; X) of all step functions from [0, T] into X (taking closure with respect to the supremum norm in the space B([0, T]; X) of all bounded functions from [0, T] into X).

Properties of regulated functions

Let Reg([0, T]; X) denote the set of all regulated functions f : [0, T] → X.

• Sums and scalar multiples of regulated functions are again regulated functions. In other words, Reg([0, T]; X) is a vector space
  Vector space
  A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
  
   over the same field
  Field (mathematics)
  In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
  
   K as the space X; typically, K will be the real
  Real number
  In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
  
   or complex number
  Complex number
  A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
  
  s. If X is equipped with an operation of multiplication, then products of regulated functions are again regulated functions. In other words, if X is a K-algebra
  Algebra over a field
  In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
  
  , then so is Reg([0, T]; X).

• The supremum norm is a norm
  Norm (mathematics)
  In linear algebra, functional analysis and related areas of mathematics, a norm is a function that assigns a strictly positive length or size to all vectors in a vector space, other than the zero vector...
  
   on Reg([0, T]; X), and Reg([0, T]; X) is a topological vector space
  Topological vector space
  In mathematics, a topological vector space is one of the basic structures investigated in functional analysis...
  
   with respect to the topology induced by the supremum norm.

• As noted above, Reg([0, T]; X) is the closure in B([0, T]; X) of Step([0, T]; X) with respect to the supremum norm.

• If X is a Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
  , then Reg([0, T]; X) is also a Banach space with respect to the supremum norm.

• Reg([0, T]; R) forms an infinite-dimensional real Banach algebra
  Banach algebra
  In mathematics, especially functional analysis, a Banach algebra, named after Stefan Banach, is an associative algebra A over the real or complex numbers which at the same time is also a Banach space...
  
  : finite linear combinations and products of regulated functions are again regulated functions.

• Since a continuous function
  Continuous function
  In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
  
   defined on a compact space
  Compact space
  In mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
  
   (such as [0, T]) is automatically uniformly continuous, every continuous function f : [0, T] → X is also regulated. In fact, with respect to the supremum norm, the space C⁰([0, T]; X) of continuous functions is a closed
  Closed set
  In geometry, topology, and related branches of mathematics, a closed set is a set whose complement is an open set. In a topological space, a closed set can be defined as a set which contains all its limit points...
  
   linear subspace
  Linear subspace
  The concept of a linear subspace is important in linear algebra and related fields of mathematics.A linear subspace is usually called simply a subspace when the context serves to distinguish it from other kinds of subspaces....
  
   of Reg([0, T]; X).

• If X is a Banach space
  Banach space
  In mathematics, Banach spaces is the name for complete normed vector spaces, one of the central objects of study in functional analysis. A complete normed vector space is a vector space V with a norm ||·|| such that every Cauchy sequence in V has a limit in V In mathematics, Banach spaces is the...
  
  , then the space BV([0, T]; X) of functions of bounded variation
  Bounded variation
  In mathematical analysis, a function of bounded variation, also known as a BV function, is a real-valued function whose total variation is bounded : the graph of a function having this property is well behaved in a precise sense...
  
   forms a dense
  Dense set
  In topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
  
   linear subspace of Reg([0, T]; X):

• If X is a Banach space, then a function f : [0, T] → X is regulated if and only if
  If and only if
  In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
  
   it is of bounded φ-variation for some φ:

• If X is a separable Hilbert space
  Hilbert space
  The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
  
  , then Reg([0, T]; X) satisfies a compactness theorem known as the Fraňková-Helly selection theorem
  Franková-Helly selection theorem
  In mathematics, the Fraňková–Helly selection theorem is a generalisation of Helly's selection theorem for functions of bounded variation to the case of regulated functions...
  
  .

• The set of discontinuities of a regulated function is countable: to see this it is sufficient to note that given 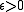, the set of points at which the right and left limits differ by more than is finite. In particular, the discontinuity set has measure zero, from which it follows that a regulated function has a well-defined Riemann integral
  Riemann integral
  In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
  
  .

• The integral, as defined on step functions in the obvious way, extends naturally to Reg([0, T]; X) by defining the integral of a regulated function to be the limit of the integrals of any sequence of step functions converging uniformly to it. This extension is well-defined
  Well-defined
  In mathematics, well-definition is a mathematical or logical definition of a certain concept or object which uses a set of base axioms in an entirely unambiguous way and satisfies the properties it is required to satisfy. Usually definitions are stated unambiguously, and it is clear they satisfy...
  
   and satisfies all of the usual properties of an integral. In particular, the regulated integral
  Regulated integral
  In mathematics, the regulated integral is a definition of integration for regulated functions, which are defined to be uniform limits of step functions. The use of the regulated integral instead of the Riemann integral has been advocated by Nicolas Bourbaki and Jean Dieudonné.-Definition on step...
  
  
  • is a bounded linear function from Reg([0, T]; X) to X; hence, in the case X = R, the integral is an element of the space that is dual to Reg([0, T]; R);
  • agrees with the Riemann integral
    Riemann integral
    In the branch of mathematics known as real analysis, the Riemann integral, created by Bernhard Riemann, was the first rigorous definition of the integral of a function on an interval. The Riemann integral is unsuitable for many theoretical purposes...
    
    .