Functional decomposition
Encyclopedia
Functional decomposition refers broadly to the process of resolving a functional
relationship into its constituent parts in such a way that the original function can be reconstructed (i.e., recomposed) from those parts by function composition
. In general, this process of decomposition is undertaken either for the purpose of gaining insight into the identity of the constituent components (which may reflect individual physical processes of interest, for example), or for the purpose of obtaining a compressed representation of the global function, a task which is feasible only when the constituent processes possess a certain level of modularity (i.e., independence or non-interaction).
For a multivariate function 
, functional decomposition generally refers to a process of identifying a set of functions 
such that
where
is some other function. Thus, we would say that the function 
is decomposed into functions 
. This process is intrinsically hierarchical in the sense that we can (and often do) seek to further decompose the functions 
into a collection of constituent functions 
such that
where
is some other function. Decompositions of this kind are interesting and important for a wide variety of reasons. In general, functional decompositions are worthwhile when there is a certain "sparseness" in the dependency structure; that is, when constituent functions are found to depend on approximately disjoint sets of variables. Thus, for example, if we can obtain a decomposition of 
into a hierarchical composition of functions 
such that 
, 
, 
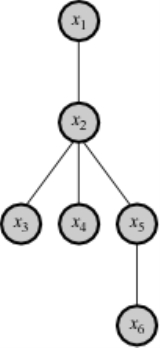
, as shown in the figure at right, this would probably be considered a highly valuable decomposition.
requires storing 
values, the value of the function for each element in the Cartesian product
, i.e., each of the 1024 possible combinations for 
. However, if the decomposition into 
given above is possible, then 
requires storing 4 values, 
requires storing 
values, and 
again requires storing just 4 values. So in virtue of the decomposition, we need store only 
values rather than 1024 values, a dramatic savings.
Intuitively, this reduction in representation size is achieved simply because each variable depends only on a subset of the other variables. Thus, variable 
only depends directly on variable 
, rather than depending on the entire set of variables. We would say that variable 
screens off variable 
from the rest of the world. Practical examples of this phenomenon surround us, as discussed in the "Philosophical Considerations" below, but let's just consider the particular case of "northbound traffic on the West Side Highway
." Let us assume this variable (
) takes on three possible values of {"moving slow", "moving deadly slow", "not moving at all"}. Now let's say variable 
depends on two other variables, "weather" with values of {"sun", "rain", "snow"}, and "GW Bridge traffic" with values {"10mph", "5mph", "1mph"}. The point here is that while there are certainly many secondary variables that affect the weather variable (e.g., low pressure system over Canada, butterfly flapping
in Japan, etc.) and the Bridge traffic variable (e.g., an accident on I-95
, presidential motorcade, etc.) all these other secondary variables are not directly relevant to the West Side Highway traffic. All we need (hypothetically) in order to predict the West Side Highway traffic is the weather and the GW Bridge traffic, because these two variables screen off West Side Highway traffic from all other potential influences. That is, all other influences act through them.
Outside of purely mathematical considerations, perhaps the greatest value of functional decomposition is the insight it provides into the structure of the world. When a functional decomposition can be achieved, this provides ontological information about what structures actually exist in the world, and how they can be predicted and manipulated. For example, in the illustration above, if it is learned that
depends directly only on 
, this means that for purposes of prediction of 
, it suffices to know only 
. Moreover, interventions to influence 
can be taken directly on 
, and nothing additional can be gained by intervening on variables 
, since these only act through 
in any case.
and Western Philosophy
is that the Eastern philosophers tended to espouse ideas favoring holism
while the Western thinkers tended to espouse ideas favoring reductionism
. While this distinction between East and West — like other such philosophical distinctions that have been drawn (e.g., realism
vs. anti-realism
) — almost certainly simplifies matters too much, there is still a kernel of truth to be had. Some examples of the Eastern holistic spirit:
The Western tradition, from its origins among the Greek philosophers, preferred a position in which drawing correct distinctions, divisions, and contrasts was considered the very pinnacle of insight. In the Aristotelian
/Porphyrian
worldview, to be able to distinguish (via strict proof) which qualities of a thing represent its essence
vs. property
vs. accident
vs. definition
, and by virtue of this formal description to segregate that entity into its proper place in the taxonomy of nature — this was to achieve the very height of wisdom.
An important notion that always arises in connection with hierarchies is modularity, which is effectively implied by the sparseness of connections in hierarchical topologies. In physical systems, a module is generally a set of interacting components that relates to the external world via a very limited interface, thus concealing most aspects of its internal structure. As a result, modifications that are made to the internals of a module (to improve efficiency for example) do not necessarily create a ripple effect through the rest of the system . This feature makes the effective use of modularity a centerpiece of all good software and hardware engineering, notably object oriented programming . Other examples of the use of hierarchy in the manufacture of artifacts, including computer software , are too obvious to bear mention.
It has been proposed that perception itself is a process of hierarchical decomposition , and that phenomena which are not essentially hierarchical in nature may not even be "theoretically intelligible" to the human mind . In Simon's words,
, linear systems, and database systems.
and machine learning
. Hierarchical model induction techniques such as Logic circuit minimization, decision trees, decision rules
, grammatical inference, hierarchical clustering
, and quadtree decomposition are all examples of function decomposition. A review of other applications and function decomposition can be found in , which also presents methods based on information theory
and graph theory
.
Many statistical inference methods can be thought of as implementing a function decomposition process in the presence of noise; that is, where functional dependencies are only expected to hold approximately. Among such models are mixture models and the recently popular methods referred to as "causal decompositions" or Bayesian networks.
However, while perfect functional decomposition is usually impossible, the spirit lives on in a large number of statistical methods that are equipped to deal with noisy systems. When a natural or artificial system is intrinsically hierarchical, the joint distribution
on system variables should provide evidence of this hierarchical structure. The task of an observer who seeks to understand the system is then to infer the hierarchical structure from observations of these variables. This is the notion behind the hierarchical decomposition of a joint distribution, the attempt to recover something of the intrinsic hierarchical structure which generated that joint distribution.
As an example, Bayesian network
methods attempt to decompose a joint distribution along its causal fault lines, thus "cutting nature at its seams". The essential motivation behind these methods is again that within most systems (natural or artificial), relatively few components/events interact with one another directly on equal footing . Rather, one observes pockets of dense connections (direct interactions) among small subsets of components, but only loose connections between these densely connected subsets. There is thus a notion of "causal proximity" in physical systems under which variables naturally precipitate into small clusters. Identifying these clusters and using them to represent the joint provides the basis for great efficiency of storage (relative to the full joint distribution) as well as for potent inference algorithms.
, where a major goal is to modularize processes to the greatest extent possible. For example, a library management system may be broken up into an inventory module, a patron information module, and a fee assessment module. In the early decades of computer programming, this was manifested as the "art of subroutining," as it was called by some prominent practitioners.
systems, such as LTI systems
. The input signal to an LTI system can be expressed as a function,
. Then 
can be decomposed into a linear combination of other functions, called component signals:
Here,
are the component signals. Note that 
are constants. This decomposition aids in analysis, because now the output of the system can be expressed in terms of the components of the input. If we let 
represent the effect of the system, then the output signal is 
, which can be expressed as:
In other words, the system can be seen as acting separately on each of the components of the input signal. Commonly used examples of this type of decomposition are the Fourier series
and the Fourier transform
.
This exercise forces each part of the system to have a pure function
. When a system is composed of pure functions, they can be reused, or replaced. A usual side effect is that the interfaces between blocks become simple and generic. Since the interfaces usually become simple, it is easier to replace a pure function with a related, similar function.
For example, say that one needs to make a stereo
system. One might functionally decompose this into speakers
, amplifier
, a tape deck and a front panel. Later, when a different model needs an audio CD, it can probably fit the same interfaces.
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
relationship into its constituent parts in such a way that the original function can be reconstructed (i.e., recomposed) from those parts by function composition
Function composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
. In general, this process of decomposition is undertaken either for the purpose of gaining insight into the identity of the constituent components (which may reflect individual physical processes of interest, for example), or for the purpose of obtaining a compressed representation of the global function, a task which is feasible only when the constituent processes possess a certain level of modularity (i.e., independence or non-interaction).
Basic mathematical definition
, functional decomposition generally refers to a process of identifying a set of functions such thatwhere
is some other function. Thus, we would say that the function is decomposed into functions . This process is intrinsically hierarchical in the sense that we can (and often do) seek to further decompose the functions into a collection of constituent functions such thatwhere
is some other function. Decompositions of this kind are interesting and important for a wide variety of reasons. In general, functional decompositions are worthwhile when there is a certain "sparseness" in the dependency structure; that is, when constituent functions are found to depend on approximately disjoint sets of variables. 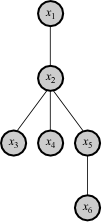Thus, for example, if we can obtain a decomposition of into a hierarchical composition of functions such that , , , as shown in the figure at right, this would probably be considered a highly valuable decomposition.Motivation for decomposition
As to why the decomposition is valuable, the reason is twofold. Firstly, decomposition of a function into non-interacting components generally permits more economical representations of the function. For example, on a set of quaternary (i.e., 4-ary) variables, representing the full function requires storing values, the value of the function for each element in the Cartesian productCartesian product
In mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
, i.e., each of the 1024 possible combinations for . However, if the decomposition into given above is possible, then requires storing 4 values, requires storing values, and again requires storing just 4 values. So in virtue of the decomposition, we need store only values rather than 1024 values, a dramatic savings. only depends directly on variable , rather than depending on the entire set of variables. We would say that variable screens off variable from the rest of the world. Practical examples of this phenomenon surround us, as discussed in the "Philosophical Considerations" below, but let's just consider the particular case of "northbound traffic on the West Side HighwayWest Side Highway
The West Side Highway is a mostly surface section of New York State Route 9A that runs from West 72nd Street along the Hudson River to the southern tip of Manhattan. It replaced the West Side Elevated Highway, built between 1929 and 1951, which was shut down in 1973 due to neglect and lack of...
." Let us assume this variable (
) takes on three possible values of {"moving slow", "moving deadly slow", "not moving at all"}. Now let's say variable depends on two other variables, "weather" with values of {"sun", "rain", "snow"}, and "GW Bridge traffic" with values {"10mph", "5mph", "1mph"}. The point here is that while there are certainly many secondary variables that affect the weather variable (e.g., low pressure system over Canada, butterfly flappingButterfly effect
In chaos theory, the butterfly effect is the sensitive dependence on initial conditions; where a small change at one place in a nonlinear system can result in large differences to a later state...
in Japan, etc.) and the Bridge traffic variable (e.g., an accident on I-95
Interstate 95 in New York
Interstate 95 is a part of the Interstate Highway System that runs from Miami, Florida, to the Canada – United States border near Houlton, Maine. In the U.S. state of New York, I-95 extends from the George Washington Bridge in New York City to the Connecticut state line at Port Chester...
, presidential motorcade, etc.) all these other secondary variables are not directly relevant to the West Side Highway traffic. All we need (hypothetically) in order to predict the West Side Highway traffic is the weather and the GW Bridge traffic, because these two variables screen off West Side Highway traffic from all other potential influences. That is, all other influences act through them.
Outside of purely mathematical considerations, perhaps the greatest value of functional decomposition is the insight it provides into the structure of the world. When a functional decomposition can be achieved, this provides ontological information about what structures actually exist in the world, and how they can be predicted and manipulated. For example, in the illustration above, if it is learned that
depends directly only on , this means that for purposes of prediction of , it suffices to know only . Moreover, interventions to influence can be taken directly on , and nothing additional can be gained by intervening on variables , since these only act through in any case.Philosophical considerations
The philosophical antecedents and ramifications of functional decomposition are quite broad, as functional decomposition in one guise or another underlies all of modern science. Here we review just a few of these philosophical considerations.Reductionist tradition
One of the major distinctions that is often drawn between Eastern philosophyEastern philosophy
Eastern philosophy includes the various philosophies of Asia, including Chinese philosophy, Iranian philosophy, Japanese philosophy, Indian philosophy and Korean philosophy...
and Western Philosophy
Western philosophy
Western philosophy is the philosophical thought and work of the Western or Occidental world, as distinct from Eastern or Oriental philosophies and the varieties of indigenous philosophies....
is that the Eastern philosophers tended to espouse ideas favoring holism
Holism
Holism is the idea that all the properties of a given system cannot be determined or explained by its component parts alone...
while the Western thinkers tended to espouse ideas favoring reductionism
Reductionism
Reductionism can mean either an approach to understanding the nature of complex things by reducing them to the interactions of their parts, or to simpler or more fundamental things or a philosophical position that a complex system is nothing but the sum of its parts, and that an account of it can...
. While this distinction between East and West — like other such philosophical distinctions that have been drawn (e.g., realism
Philosophical realism
Contemporary philosophical realism is the belief that our reality, or some aspect of it, is ontologically independent of our conceptual schemes, linguistic practices, beliefs, etc....
vs. anti-realism
Anti-realism
In analytic philosophy, the term anti-realism is used to describe any position involving either the denial of an objective reality of entities of a certain type or the denial that verification-transcendent statements about a type of entity are either true or false...
) — almost certainly simplifies matters too much, there is still a kernel of truth to be had. Some examples of the Eastern holistic spirit:
- "Open your mouth, increase your activities, start making distinctions between things, and you'll toil forever without hope." — The Tao Te ChingTao Te ChingThe Tao Te Ching, Dao De Jing, or Daodejing , also simply referred to as the Laozi, whose authorship has been attributed to Laozi, is a Chinese classic text...
of Lao Tzu (Brian Browne Walker, translator) - "It's a hard job for [people] to see the meaning of the fact that everything, including ourselves, depends on everything else and has no permanent self-existence." — Majjhima NikayaMajjhima NikayaThe Majjhima Nikaya is a Buddhist scripture, the second of the five nikayas, or collections, in the Sutta Pitaka, which is one of the "three baskets" that compose the Pali Tipitaka of Theravada Buddhism...
(Anne Bankroft, translator) - "A name is imposed on what is thought to be a thing or a state and this divides it from other things and other states. But when you pursue what lies behind the name, you find a greater and greater subtlety that has no divisions..." — Visuddhi Magga (Anne Bankroft, translator)
The Western tradition, from its origins among the Greek philosophers, preferred a position in which drawing correct distinctions, divisions, and contrasts was considered the very pinnacle of insight. In the Aristotelian
Aristotelianism
Aristotelianism is a tradition of philosophy that takes its defining inspiration from the work of Aristotle. The works of Aristotle were initially defended by the members of the Peripatetic school, and, later on, by the Neoplatonists, who produced many commentaries on Aristotle's writings...
/Porphyrian
Porphyry (philosopher)
Porphyry of Tyre , Porphyrios, AD 234–c. 305) was a Neoplatonic philosopher who was born in Tyre. He edited and published the Enneads, the only collection of the work of his teacher Plotinus. He also wrote many works himself on a wide variety of topics...
worldview, to be able to distinguish (via strict proof) which qualities of a thing represent its essence
Essence
In philosophy, essence is the attribute or set of attributes that make an object or substance what it fundamentally is, and which it has by necessity, and without which it loses its identity. Essence is contrasted with accident: a property that the object or substance has contingently, without...
vs. property
Property (philosophy)
In modern philosophy, logic, and mathematics a property is an attribute of an object; a red object is said to have the property of redness. The property may be considered a form of object in its own right, able to possess other properties. A property however differs from individual objects in that...
vs. accident
Accident (philosophy)
Accident, as used in philosophy, is an attribute which may or may not belong to a subject, without affecting its essence. The word "accident" has been employed throughout the history of philosophy with several distinct meanings....
vs. definition
Intensional definition
In logic and mathematics, an intensional definition gives the meaning of a term by specifying all the properties required to come to that definition, that is, the necessary and sufficient conditions for belonging to the set being defined....
, and by virtue of this formal description to segregate that entity into its proper place in the taxonomy of nature — this was to achieve the very height of wisdom.
Characteristics of hierarchy and modularity
In natural or artificial systems that require components to be integrated in some fashion, but where the number of components exceeds what could reasonably be fully interconnected (due to exponential growth in number of connections), one often finds that some degree of hierarchicality must be employed in the solution. The general advantages of sparse hierarchical systems over densely-connected systems—and quantitative estimates of these advantage—are presented by . In prosaic terms, a hierarchy is "a collection of elements that combine lawfully into complex wholes which depend for their properties upon those of their constituent parts," and wherein novelty is "fundamentally combinatorial, iterative, and transparent" .An important notion that always arises in connection with hierarchies is modularity, which is effectively implied by the sparseness of connections in hierarchical topologies. In physical systems, a module is generally a set of interacting components that relates to the external world via a very limited interface, thus concealing most aspects of its internal structure. As a result, modifications that are made to the internals of a module (to improve efficiency for example) do not necessarily create a ripple effect through the rest of the system . This feature makes the effective use of modularity a centerpiece of all good software and hardware engineering, notably object oriented programming . Other examples of the use of hierarchy in the manufacture of artifacts, including computer software , are too obvious to bear mention.
Inevitability of hierarchy and modularity
There are many compelling arguments regarding the prevalence and necessity of hierarchy/modularity in nature . points out that among evolving systems, only those that can manage to obtain and then reuse stable subassemblies (modules) are likely to be able to search through the fitness landscape with a reasonably quick pace; thus, Simon submits that "among possible complex forms, hierarchies are the ones that have the time to evolve." This line of thinking has led to the even stronger claim that although "we do not know what forms of life have evolved on other planets in the universe, ... we can safely assume that 'wherever there is life, it must be hierarchically organized'" . This would be a fortunate state of affairs since the existence of simple and isolable subsystems is thought to be a precondition for successful science . In any case, experience certainly seems to indicate that much of the world possesses hierarchical structure.It has been proposed that perception itself is a process of hierarchical decomposition , and that phenomena which are not essentially hierarchical in nature may not even be "theoretically intelligible" to the human mind . In Simon's words,
Applications
Practical applications of functional decomposition are found in Bayesian networks, structural equation modelingStructural equation modeling
Structural equation modeling is a statistical technique for testing and estimating causal relations using a combination of statistical data and qualitative causal assumptions...
, linear systems, and database systems.
Knowledge representation
Processes related to functional decomposition are prevalent throughout the fields of knowledge representationKnowledge representation
Knowledge representation is an area of artificial intelligence research aimed at representing knowledge in symbols to facilitate inferencing from those knowledge elements, creating new elements of knowledge...
and machine learning
Machine learning
Machine learning, a branch of artificial intelligence, is a scientific discipline concerned with the design and development of algorithms that allow computers to evolve behaviors based on empirical data, such as from sensor data or databases...
. Hierarchical model induction techniques such as Logic circuit minimization, decision trees, decision rules
Decision rules
A set of decision rules is the verbal equivalent of a graphical decision tree, which specifies class membership based on a hierarchical sequence of decisions...
, grammatical inference, hierarchical clustering
Hierarchical clustering
In statistics, hierarchical clustering is a method of cluster analysis which seeks to build a hierarchy of clusters. Strategies for hierarchical clustering generally fall into two types:...
, and quadtree decomposition are all examples of function decomposition. A review of other applications and function decomposition can be found in , which also presents methods based on information theory
Information theory
Information theory is a branch of applied mathematics and electrical engineering involving the quantification of information. Information theory was developed by Claude E. Shannon to find fundamental limits on signal processing operations such as compressing data and on reliably storing and...
and graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
.
Many statistical inference methods can be thought of as implementing a function decomposition process in the presence of noise; that is, where functional dependencies are only expected to hold approximately. Among such models are mixture models and the recently popular methods referred to as "causal decompositions" or Bayesian networks.
Machine learning
In practical scientific applications, it is almost never possible to achieve perfect functional decomposition because of the incredible complexity of the systems under study. this complexity is manifested in the presence of "noise," which is just a designation for all the unwanted and untraceable influences on our observations.However, while perfect functional decomposition is usually impossible, the spirit lives on in a large number of statistical methods that are equipped to deal with noisy systems. When a natural or artificial system is intrinsically hierarchical, the joint distribution
Joint distribution
In the study of probability, given two random variables X and Y that are defined on the same probability space, the joint distribution for X and Y defines the probability of events defined in terms of both X and Y...
on system variables should provide evidence of this hierarchical structure. The task of an observer who seeks to understand the system is then to infer the hierarchical structure from observations of these variables. This is the notion behind the hierarchical decomposition of a joint distribution, the attempt to recover something of the intrinsic hierarchical structure which generated that joint distribution.
As an example, Bayesian network
Bayesian network
A Bayesian network, Bayes network, belief network or directed acyclic graphical model is a probabilistic graphical model that represents a set of random variables and their conditional dependencies via a directed acyclic graph . For example, a Bayesian network could represent the probabilistic...
methods attempt to decompose a joint distribution along its causal fault lines, thus "cutting nature at its seams". The essential motivation behind these methods is again that within most systems (natural or artificial), relatively few components/events interact with one another directly on equal footing . Rather, one observes pockets of dense connections (direct interactions) among small subsets of components, but only loose connections between these densely connected subsets. There is thus a notion of "causal proximity" in physical systems under which variables naturally precipitate into small clusters. Identifying these clusters and using them to represent the joint provides the basis for great efficiency of storage (relative to the full joint distribution) as well as for potent inference algorithms.
Computer programming and software engineering
For most of the same reasons already stipulated, functional decomposition has a prominent role in computer programmingComputer programming
Computer programming is the process of designing, writing, testing, debugging, and maintaining the source code of computer programs. This source code is written in one or more programming languages. The purpose of programming is to create a program that performs specific operations or exhibits a...
, where a major goal is to modularize processes to the greatest extent possible. For example, a library management system may be broken up into an inventory module, a patron information module, and a fee assessment module. In the early decades of computer programming, this was manifested as the "art of subroutining," as it was called by some prominent practitioners.
Signal processing
Functional decomposition is used in the analysis of many signal processingSignal processing
Signal processing is an area of systems engineering, electrical engineering and applied mathematics that deals with operations on or analysis of signals, in either discrete or continuous time...
systems, such as LTI systems
LTI system theory
Linear time-invariant system theory, commonly known as LTI system theory, comes from applied mathematics and has direct applications in NMR spectroscopy, seismology, circuits, signal processing, control theory, and other technical areas. It investigates the response of a linear and time-invariant...
. The input signal to an LTI system can be expressed as a function,
. Then can be decomposed into a linear combination of other functions, called component signals:
Here,
are the component signals. Note that are constants. This decomposition aids in analysis, because now the output of the system can be expressed in terms of the components of the input. If we let represent the effect of the system, then the output signal is , which can be expressed as:
In other words, the system can be seen as acting separately on each of the components of the input signal. Commonly used examples of this type of decomposition are the Fourier series
Fourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
and the Fourier transform
Fourier transform
In mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
.
Systems engineering
Functional decomposition of engineering systems is a method for analyzing engineered systems. The basic idea is to try to divide a system in such a way that each block of the block diagram can be described without an "and" or "or" in the description.This exercise forces each part of the system to have a pure function
Role
A role or a social role is a set of connected behaviours, rights and obligations as conceptualised by actors in a social situation. It is an expected or free or continuously changing behaviour and may have a given individual social status or social position...
. When a system is composed of pure functions, they can be reused, or replaced. A usual side effect is that the interfaces between blocks become simple and generic. Since the interfaces usually become simple, it is easier to replace a pure function with a related, similar function.
For example, say that one needs to make a stereo
Boombox
Boombox is a colloquial expression for a portable cassette or CD player. Other terms known are ghetto blaster, jambox, or radio-cassette. It is a device capable of receiving radio stations and playing recorded music , usually at relatively high volume...
system. One might functionally decompose this into speakers
Loudspeaker
A loudspeaker is an electroacoustic transducer that produces sound in response to an electrical audio signal input. Non-electrical loudspeakers were developed as accessories to telephone systems, but electronic amplification by vacuum tube made loudspeakers more generally useful...
, amplifier
Amplifier
Generally, an amplifier or simply amp, is a device for increasing the power of a signal.In popular use, the term usually describes an electronic amplifier, in which the input "signal" is usually a voltage or a current. In audio applications, amplifiers drive the loudspeakers used in PA systems to...
, a tape deck and a front panel. Later, when a different model needs an audio CD, it can probably fit the same interfaces.
See also
- Bayesian networks
- Database normalizationDatabase normalizationIn the design of a relational database management system , the process of organizing data to minimize redundancy is called normalization. The goal of database normalization is to decompose relations with anomalies in order to produce smaller, well-structured relations...
- Function compositionFunction compositionIn mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
- Inductive inferenceInductive inferenceAround 1960, Ray Solomonoff founded the theory of universal inductive inference, the theory of prediction based on observations; for example, predicting the next symbol based upon a given series of symbols...
- Knowledge representationKnowledge representationKnowledge representation is an area of artificial intelligence research aimed at representing knowledge in symbols to facilitate inferencing from those knowledge elements, creating new elements of knowledge...