Gauss-Manin connection
Encyclopedia
In mathematics
, the Gauss–Manin connection, introduced by , is a connection
on a certain vector bundle
over a family of algebraic varieties
. The base space is taken to be the set of parameters defining the family, and the fibers are taken to be the de Rham cohomology
group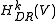
of the fibers V.
Flat sections of the bundle are described by differential equation
s; the best-known of these is the Picard–Fuchs equation, which arises when the family of varieties is taken to be the family of elliptic curve
s. In intuitive terms, when the family is locally trivial, cohomology classes can be moved from one fiber in the family to nearby fibers, providing the 'flat section' concept in purely topological terms. The existence of the connection is to be inferred from the flat sections.
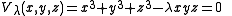
be the projective variety describing the elliptic curve
. Here,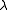
is a free parameter describing the curve; it is an element of the complex projective line (the family of hypersurfaces in n − 1 dimensions of degree n, defined analogously, has been intensively studied in recent years, in connection with the modularity theorem and its extensions). Thus, the base space of the bundle is taken to be the projective line. For a fixed 
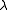in the base space, consider an element 
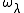of the associated de Rham cohomology group
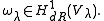
Each such element corresponds to a period of the elliptic curve. The cohomology is two-dimensional. The Gauss–Manin connection corresponds to the second-order differential equation
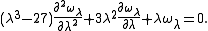
theory, the existence of such equations is subsumed in a general discussion of the direct image.
concept of transcendence theory
, for meromorphic function solutions. The Bombieri-Dwork conjecture, also attributed to André, which is given in more than one version, postulates a converse direction: solutions as G-functions, or p-curvature nilpotent mod p for almost all p, means an equation "arises from geometry".
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Gauss–Manin connection, introduced by , is a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
on a certain vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over a family of algebraic varieties
Algebraic variety
In mathematics, an algebraic variety is the set of solutions of a system of polynomial equations. Algebraic varieties are one of the central objects of study in algebraic geometry...
. The base space is taken to be the set of parameters defining the family, and the fibers are taken to be the de Rham cohomology
De Rham cohomology
In mathematics, de Rham cohomology is a tool belonging both to algebraic topology and to differential topology, capable of expressing basic topological information about smooth manifolds in a form particularly adapted to computation and the concrete representation of cohomology classes...
group
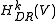of the fibers V.Flat sections of the bundle are described by differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
s; the best-known of these is the Picard–Fuchs equation, which arises when the family of varieties is taken to be the family of elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
s. In intuitive terms, when the family is locally trivial, cohomology classes can be moved from one fiber in the family to nearby fibers, providing the 'flat section' concept in purely topological terms. The existence of the connection is to be inferred from the flat sections.
Example
A commonly cited example is the Dwork construction of the Picard–Fuchs equation. Let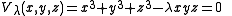be the projective variety describing the elliptic curve
Elliptic curve
In mathematics, an elliptic curve is a smooth, projective algebraic curve of genus one, on which there is a specified point O. An elliptic curve is in fact an abelian variety — that is, it has a multiplication defined algebraically with respect to which it is a group — and O serves as the identity...
. Here,
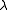is a free parameter describing the curve; it is an element of the complex projective line (the family of hypersurfaces in n − 1 dimensions of degree n, defined analogously, has been intensively studied in recent years, in connection with the modularity theorem and its extensions). Thus, the base space of the bundle is taken to be the projective line. For a fixed 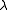in the base space, consider an element 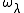of the associated de Rham cohomology group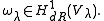Each such element corresponds to a period of the elliptic curve. The cohomology is two-dimensional. The Gauss–Manin connection corresponds to the second-order differential equation
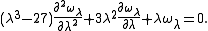
D-module explanation
In the more abstract setting of D-moduleD-module
In mathematics, a D-module is a module over a ring D of differential operators. The major interest of such D-modules is as an approach to the theory of linear partial differential equations...
theory, the existence of such equations is subsumed in a general discussion of the direct image.
Equations "arising from geometry"
The whole class of Gauss–Manin connections has been used to try for formulate the concept of differential equations that "arise from geometry". In connection with the Grothendieck p-curvature conjecture, Nicholas Katz proved that the class of Gauss–Manin connections with algebraic number coefficients satisfies the conjecture. This result is directly connected with the G-functionSiegel G-function
In mathematics, a Siegel G-function is a class of functions in transcendence theory introduced by C. L. Siegel. They satisfy a linear differential equation with polynomial coefficients, and the coefficients of their power series expansion lie in a fixed algebraic number field and have heights of...
concept of transcendence theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
, for meromorphic function solutions. The Bombieri-Dwork conjecture, also attributed to André, which is given in more than one version, postulates a converse direction: solutions as G-functions, or p-curvature nilpotent mod p for almost all p, means an equation "arises from geometry".