Gent (hyperelastic model)
Encyclopedia
The Gent hyperelastic material
model is a phenomenological model of rubber elasticity
that is based on the concept of limiting chain extensibility. In this model, the strain energy density function
is designed such that it has a singularity
when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value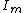
.
The strain energy density function for the Gent model is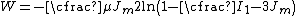
where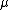
is the shear modulus and 
.
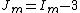In the limit where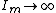
, the Gent model reduces to the Neo-Hookean solid
model. This can be seen by expressing the Gent model in the form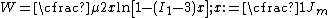
A Taylor series expansion of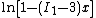
around 
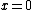and taking the limit as 
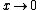leads to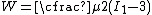
which is the expression for the strain energy density of a Neo-Hookean solid.
Several compressible versions of the Gent model have been designed. One such model has the form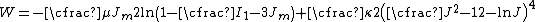
where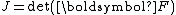
, 
is the bulk modulus
, and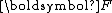
is the deformation gradient.
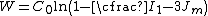
For the model to be consistent with linear elasticity
, the following condition has to be satisfied:
where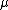
is the shear modulus of the material.
Now, at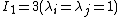
,
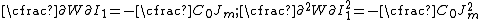
Therefore, the consistency condition for the Gent model is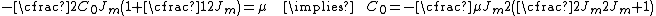
The Gent model assumes that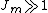
so that 
.
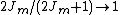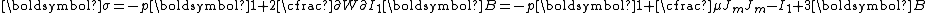
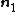-direction, the principal stretches are 
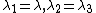. From incompressibility 
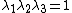. Hence 
.
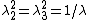Therefore,
The left Cauchy-Green deformation tensor can then be expressed as
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have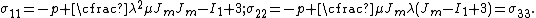
If
, we have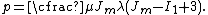
Therefore,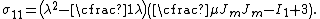
The engineering strain
is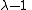
. The engineering stress
is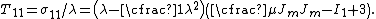
and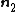 
directions, the principal stretches are 
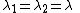. From incompressibility 
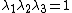. Hence 
.
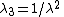Therefore,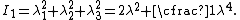
The left Cauchy-Green deformation tensor can then be expressed as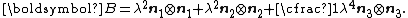
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have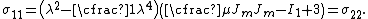
The engineering strain
is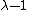
. The engineering stress
is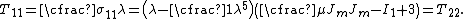
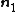directions with the 
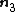direction constrained, the principal stretches are 
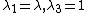. From incompressibility 
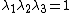. Hence 
.
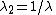Therefore,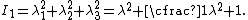
The left Cauchy-Green deformation tensor can then be expressed as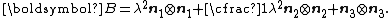
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have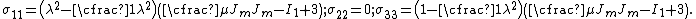
The engineering strain
is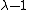
. The engineering stress
is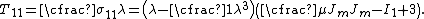
deformation has the form
where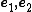
are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by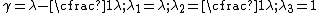
In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as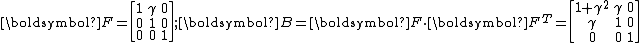
Therefore,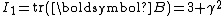
and the Cauchy stress is given by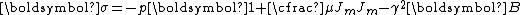
In matrix form,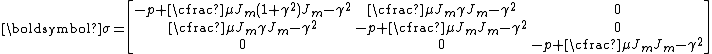
Hyperelastic material
A hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
model is a phenomenological model of rubber elasticity
Rubber Elasticity
Rubber elasticity, a well-known example of hyperelasticity, describes the mechanical behavior of many polymers, especially those with crosslinking. Invoking the theory of rubber elasticity, one considers a polymer chain in a crosslinked network as an entropic spring. When the chain is stretched,...
that is based on the concept of limiting chain extensibility. In this model, the strain energy density function
Strain energy density function
A strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
is designed such that it has a singularity
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
when the first invariant of the left Cauchy-Green deformation tensor reaches a limiting value
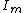.The strain energy density function for the Gent model is
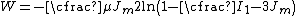
where
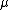is the shear modulus and 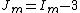.In the limit where
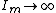, the Gent model reduces to the Neo-Hookean solidNeo-Hookean solid
A Neo-Hookean solid is a hyperelastic material model, similar to Hooke's law, that can be used for predicting the nonlinear stress-strain behavior of materials undergoing large deformations. The model was proposed by Ronald Rivlin in 1948. In contrast to linear elastic materials, a the...
model. This can be seen by expressing the Gent model in the form
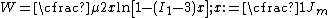
A Taylor series expansion of
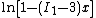around 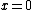and taking the limit as 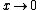leads to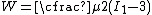which is the expression for the strain energy density of a Neo-Hookean solid.
Several compressible versions of the Gent model have been designed. One such model has the form
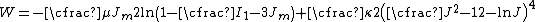
where
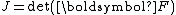, is the bulk modulusBulk modulus
The bulk modulus of a substance measures the substance's resistance to uniform compression. It is defined as the pressure increase needed to decrease the volume by a factor of 1/e...
, and
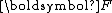is the deformation gradient.Consistency condition
We may alternatively express the Gent model in the form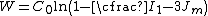For the model to be consistent with linear elasticity
Linear elasticity
Linear elasticity is the mathematical study of how solid objects deform and become internally stressed due to prescribed loading conditions. Linear elasticity models materials as continua. Linear elasticity is a simplification of the more general nonlinear theory of elasticity and is a branch of...
, the following condition has to be satisfied:
where
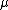is the shear modulus of the material.Now, at
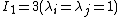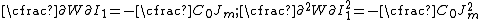
,Therefore, the consistency condition for the Gent model is
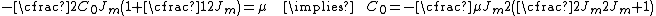
The Gent model assumes that
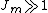so that 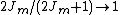.Stress-deformation relations
The Cauchy stress for the incompressible Gent model is given by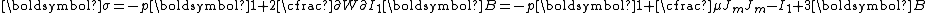Uniaxial extension
For uniaxial extension in the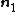-direction, the principal stretches are 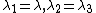. From incompressibility 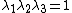. Hence 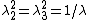.Therefore,
The left Cauchy-Green deformation tensor can then be expressed as
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
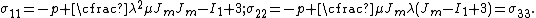
If
, we have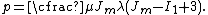Therefore,
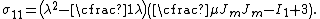
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
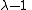. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
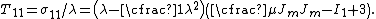
Equibiaxial extension
For equibiaxial extension in the and 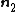directions, the principal stretches are 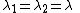. From incompressibility 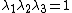. Hence 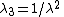.Therefore,
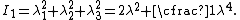
The left Cauchy-Green deformation tensor can then be expressed as
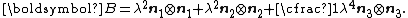
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
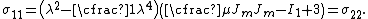
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
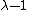. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
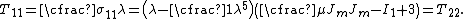
Planar extension
Planar extension tests are carried out on thin specimens which are constrained from deforming in one direction. For planar extension in the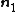 directions with the 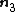direction constrained, the principal stretches are 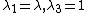. From incompressibility 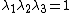. Hence 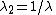.Therefore,
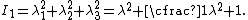
The left Cauchy-Green deformation tensor can then be expressed as
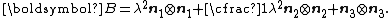
If the directions of the principal stretches are oriented with the coordinate basis vectors, we have
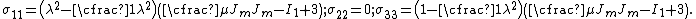
The engineering strain
Stress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
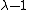. The engineering stressStress (physics)
In continuum mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are a reaction to external forces applied on the body...
is
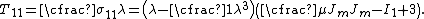
Simple shear
The deformation gradient for a simple shearSimple shear
In fluid mechanics, simple shear is a special case of deformation where only one component of velocity vectors has a non-zero value:\ V_x=f\ V_y=V_z=0And the gradient of velocity is constant and perpendicular to the velocity itself:...
deformation has the form
where
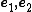are reference orthonormal basis vectors in the plane of deformation and the shear deformation is given by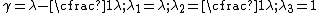In matrix form, the deformation gradient and the left Cauchy-Green deformation tensor may then be expressed as
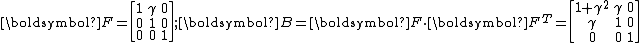
Therefore,
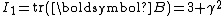
and the Cauchy stress is given by
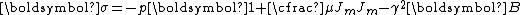
In matrix form,
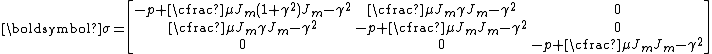
See also
- Hyperelastic materialHyperelastic materialA hyperelastic or Green elastic material is a type of constitutive model for ideally elastic material for which the stress-strain relationship derives from a strain energy density function. The hyperelastic material is a special case of a Cauchy elastic material.For many materials, linear elastic...
- Strain energy density functionStrain energy density functionA strain energy density function or stored energy density function is a scalar valued function that relates the strain energy density of a material to the deformation gradient....
- Mooney-Rivlin solid
- Finite strain theory
- Stress measuresStress measuresThe most commonly used measure of stress is the Cauchy stress. However, several other measures of stress can be defined. Some such stress measures that are widely used in continuum mechanics, particularly in the computational context, are:...