Graph pebbling
Encyclopedia
Graph pebbling is a mathematical game
and area of interest played on a graph
with pebbles on the vertices
. 'Game play' is composed of a series of pebbling moves. A pebbling move on a graph consists of taking two pebbles off one vertex and placing one on an adjacent vertex (the second removed pebble is discarded from play). π(G), the pebbling number of a graph G is the lowest natural number
n that satisfies the following condition:
For example, on a graph with 2 vertices and 1 edge connecting them the pebbling number is 2. No matter how the two pebbles are placed on the vertices of the graph it is always possible to move a pebble to any vertex in the graph. One of the central questions of graph pebbling is the value of π(G) for a given graph G.
Other topics in pebbling include cover pebbling, optimal pebbling, domination cover pebbling, bounds, and thresholds for pebbling numbers, deep graphs, and others.
. In 1989 F.R.K. Chung
introduced the concept in the literature and defined the pebbling number, π(G).
The pebbling number for a complete graph
on n vertices is easily verified to be n: If we had (n − 1) pebbles to put on the graph, then we could put 1 pebble on each vertex except one. This would make it impossible to place a pebble on the last vertex. Since this last vertex could have been the designated target vertex, the pebbling number must be greater than n − 1. If we were to add 1 more pebble to the graph there are 2 possible cases. First, we could add it to the empty vertex, which would put a pebble on every vertex. Or secondly, we could add it to one of the vertices with only 1 pebble on them. Once any vertex has 2 pebbles on it, it becomes possible to make a pebbling move to any other vertex in the complete graph.
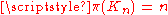where 
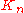is a complete graph
on n vertices.
where 
is a path graph
on n vertices.
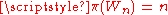where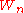 
is a wheel graph
on n vertices.
Do this for every vertex v in G. d(u, v) denotes the distance from u to v. Then the cover pebbling number is the largest s(v) that results.
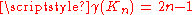where 
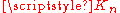is a complete graph
on n vertices.
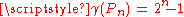where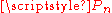 
is a path
on n vertices.
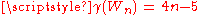where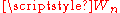 
is a wheel graph
on n vertices.
Game
A game is structured playing, usually undertaken for enjoyment and sometimes used as an educational tool. Games are distinct from work, which is usually carried out for remuneration, and from art, which is more often an expression of aesthetic or ideological elements...
and area of interest played on a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
with pebbles on the vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. 'Game play' is composed of a series of pebbling moves. A pebbling move on a graph consists of taking two pebbles off one vertex and placing one on an adjacent vertex (the second removed pebble is discarded from play). π(G), the pebbling number of a graph G is the lowest natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
n that satisfies the following condition:
Given any target or 'root' vertex in the graph and any initial configuration of n pebbles on the graph, it is possible, after a series of pebbling moves, to reach a new configuration in which the designated root vertex has one or more pebbles.
For example, on a graph with 2 vertices and 1 edge connecting them the pebbling number is 2. No matter how the two pebbles are placed on the vertices of the graph it is always possible to move a pebble to any vertex in the graph. One of the central questions of graph pebbling is the value of π(G) for a given graph G.
Other topics in pebbling include cover pebbling, optimal pebbling, domination cover pebbling, bounds, and thresholds for pebbling numbers, deep graphs, and others.
π(G) — the pebbling number of a graph
The game of pebbling was first suggested by Lagarias and Saks, as a tool for solving a particular problem in number theoryNumber theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
. In 1989 F.R.K. Chung
Fan Chung
Fan Rong K Chung Graham , known professionally as Fan Chung, is a mathematician who works mainly in the areas of spectral graph theory, extremal graph theory and random graphs, in particular...
introduced the concept in the literature and defined the pebbling number, π(G).
The pebbling number for a complete graph
Complete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on n vertices is easily verified to be n: If we had (n − 1) pebbles to put on the graph, then we could put 1 pebble on each vertex except one. This would make it impossible to place a pebble on the last vertex. Since this last vertex could have been the designated target vertex, the pebbling number must be greater than n − 1. If we were to add 1 more pebble to the graph there are 2 possible cases. First, we could add it to the empty vertex, which would put a pebble on every vertex. Or secondly, we could add it to one of the vertices with only 1 pebble on them. Once any vertex has 2 pebbles on it, it becomes possible to make a pebbling move to any other vertex in the complete graph.
π(G) for families of graphs
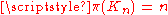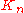where is a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on n vertices.
where is a path graphPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
on n vertices.
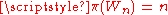where 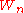is a wheel graphWheel graph
In the mathematical discipline of graph theory, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an -cycle. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle,...
on n vertices.
γ(G) — the cover pebbling number of a graph
Crull et al. introduced the concept of cover pebbling. γ(G), the cover pebbling number of a graph is the minimum number of pebbles needed so that from any initial arrangement of the pebbles, after a series of pebbling moves, it is possible to have at least 1 pebble on every vertex of a graph. Vuong and Wyckoff proved a theorem known as the stacking theorem which essentially finds the cover pebbling number for any graph: this theorem was proved at about the same time by Jonas Sjostrand.The stacking theorem
The stacking theorem states the initial configuration of pebbles that requires the most pebbles to be cover solved happens when all pebbles are placed on a single vertex. From there they state:
Do this for every vertex v in G. d(u, v) denotes the distance from u to v. Then the cover pebbling number is the largest s(v) that results.
γ(G) for families of graphs
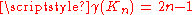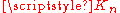where is a complete graphComplete graph
In the mathematical field of graph theory, a complete graph is a simple undirected graph in which every pair of distinct vertices is connected by a unique edge.-Properties:...
on n vertices.
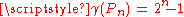where 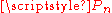is a pathPath (graph theory)
In graph theory, a path in a graph is a sequence of vertices such that from each of its vertices there is an edge to the next vertex in the sequence. A path may be infinite, but a finite path always has a first vertex, called its start vertex, and a last vertex, called its end vertex. Both of them...
on n vertices.
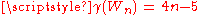where 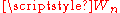is a wheel graphWheel graph
In the mathematical discipline of graph theory, a wheel graph Wn is a graph with n vertices, formed by connecting a single vertex to all vertices of an -cycle. The numerical notation for wheels is used inconsistently in the literature: some authors instead use n to refer to the length of the cycle,...
on n vertices.