
Grothendieck–Katz p-curvature conjecture
Encyclopedia
In mathematics
, the Grothendieck–Katz p-curvature conjecture is a problem on linear ordinary differential equation
s, related to differential Galois theory
and in a loose sense analogous to the result in the Chebotarev density theorem considered as the polynomial
case. It is a conjecture of Alexander Grothendieck
from the late 1960s, and apparently not published by him in any form.
The general case remains unsolved, despite recent progress; it has been linked to geometric investigations involving algebraic foliation
s.
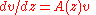
for a vector v of size n, and an n×n matrix A of algebraic function
s with algebraic number
coefficients. The question is to give a criterion for when there is a full set of algebraic function solutions, meaning a fundamental matrix (i.e. n vector solutions put into a block matrix
). For example, a classical question was for the hypergeometric equation: when does it have a pair of algebraic solutions, in terms of its parameters? The answer is known classically as Schwarz's list
. In monodromy
terms, the question is of identifying the cases of finite monodromy group.
By reformulation and passing to a larger system, the essential case is for rational functions in A and rational number coefficients. Then a necessary condition is that for almost all
prime numbers p, the system defined by reduction modulo p should also have a full set of algebraic solutions, over the finite field with p elements.
Grothendieck's conjecture is that these necessary conditions, for almost all p, should be sufficient. The connection with p-curvature is that the mod p condition stated is the same as saying the p-curvature, formed by a recurrence operation on A, is zero; so another way to say it is that p-curvature of 0 for almost all p implies enough algebraic solutions of the original equation.
techniques to show that this conjecture is essentially the same as saying that the differential Galois group G (or strictly speaking the Lie algebra
g of the algebraic group
G, which in this case is the Zariski closure of the monodromy group) can be determined by mod p information, for a certain wide class of differential equations.
and Mark Kisin
; these equations are on a locally symmetric variety X subject to some group-theoretic conditions. This work is based on the previous results of Katz for Picard–Fuchs equations (in the contemporary sense of the Gauss–Manin connection), as amplified in the Tannakian direction by André. It also applies a version of superrigidity
particular to arithmetic group
s. Other progress has been by arithmetic methods.
in 1972, in a paper where the conjecture was published. Since then, reformulations have been published. A q-analogue for difference equations has been proposed.
In responding to Kisin's talk on this work at the 2009 Colloque Grothendieck Katz gave a brief account from personal knowledge of the genesis of the conjecture. Grothendieck put it forth in public discussion in Spring 1969, but wrote nothing on the topic. He was led to the idea by foundational intuitions in the area of crystalline cohomology
, at that time being developed by his student Pierre Berthelot. In some way wishing to equate the notion of "nilpotence" in the theory of connections, with the divided power structure
technique that became standard in crystalline theory, Grothendieck produced the conjecture as a by-product.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Grothendieck–Katz p-curvature conjecture is a problem on linear ordinary differential equation
Linear differential equation
Linear differential equations are of the formwhere the differential operator L is a linear operator, y is the unknown function , and the right hand side ƒ is a given function of the same nature as y...
s, related to differential Galois theory
Differential Galois theory
In mathematics, differential Galois theory studies the Galois groups of differential equations.Whereas algebraic Galois theory studies extensions of algebraic fields, differential Galois theory studies extensions of differential fields, i.e. fields that are equipped with a derivation, D. Much of...
and in a loose sense analogous to the result in the Chebotarev density theorem considered as the polynomial
Polynomial
In mathematics, a polynomial is an expression of finite length constructed from variables and constants, using only the operations of addition, subtraction, multiplication, and non-negative integer exponents...
case. It is a conjecture of Alexander Grothendieck
Alexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
from the late 1960s, and apparently not published by him in any form.
The general case remains unsolved, despite recent progress; it has been linked to geometric investigations involving algebraic foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s.
Formulation
In a simplest possible statement, in which the p-curvature is not explicit, it can be stated in its essentials for a vector system written as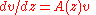
for a vector v of size n, and an n×n matrix A of algebraic function
Algebraic function
In mathematics, an algebraic function is informally a function that satisfies a polynomial equation whose coefficients are themselves polynomials with rational coefficients. For example, an algebraic function in one variable x is a solution y for an equationwhere the coefficients ai are polynomial...
s with algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
coefficients. The question is to give a criterion for when there is a full set of algebraic function solutions, meaning a fundamental matrix (i.e. n vector solutions put into a block matrix
Block matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
). For example, a classical question was for the hypergeometric equation: when does it have a pair of algebraic solutions, in terms of its parameters? The answer is known classically as Schwarz's list
Schwarz's list
In the mathematical theory of special functions, Schwarz's list or the Schwartz table is the list of 15 cases found by when hypergeometric functions can be expressed algebraically...
. In monodromy
Monodromy
In mathematics, monodromy is the study of how objects from mathematical analysis, algebraic topology and algebraic and differential geometry behave as they 'run round' a singularity. As the name implies, the fundamental meaning of monodromy comes from 'running round singly'...
terms, the question is of identifying the cases of finite monodromy group.
By reformulation and passing to a larger system, the essential case is for rational functions in A and rational number coefficients. Then a necessary condition is that for almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
prime numbers p, the system defined by reduction modulo p should also have a full set of algebraic solutions, over the finite field with p elements.
Grothendieck's conjecture is that these necessary conditions, for almost all p, should be sufficient. The connection with p-curvature is that the mod p condition stated is the same as saying the p-curvature, formed by a recurrence operation on A, is zero; so another way to say it is that p-curvature of 0 for almost all p implies enough algebraic solutions of the original equation.
Katz's formulation for the Galois group
Nicholas Katz has applied Tannakian categoryTannakian category
In mathematics, a tannakian category is a particular kind of monoidal category C, equipped with some extra structure relative to a given field K. The role of such categories C is to approximate, in some sense, the category of linear representations of an algebraic group G defined over K...
techniques to show that this conjecture is essentially the same as saying that the differential Galois group G (or strictly speaking the Lie algebra
Lie algebra
In mathematics, a Lie algebra is an algebraic structure whose main use is in studying geometric objects such as Lie groups and differentiable manifolds. Lie algebras were introduced to study the concept of infinitesimal transformations. The term "Lie algebra" was introduced by Hermann Weyl in the...
g of the algebraic group
Algebraic group
In algebraic geometry, an algebraic group is a group that is an algebraic variety, such that the multiplication and inverse are given by regular functions on the variety...
G, which in this case is the Zariski closure of the monodromy group) can be determined by mod p information, for a certain wide class of differential equations.
Progress
A wide class of cases has been proved by Benson FarbBenson Farb
Benson Stanley Farb is an American mathematician at the University of Chicago. His research fields include geometric group theory and low-dimensional topology....
and Mark Kisin
Mark Kisin
Mark Kisin is a mathematician known for work in algebraic number theory and arithmetic geometry. In particular, he is known for his contributions to the study of p-adic representations and p-adic cohomology....
; these equations are on a locally symmetric variety X subject to some group-theoretic conditions. This work is based on the previous results of Katz for Picard–Fuchs equations (in the contemporary sense of the Gauss–Manin connection), as amplified in the Tannakian direction by André. It also applies a version of superrigidity
Superrigidity
In mathematics, in the theory of discrete groups, superrigidity is a concept designed to show how a linear representation ρ of a discrete group Γ inside an algebraic group G can, under some circumstances, be as good as a representation of G itself...
particular to arithmetic group
Arithmetic group
In mathematics, an arithmetic group in a linear algebraic group G defined over a number field K is a subgroup Γ of G that is commensurable with G, where O is the ring of integers of K. Here two subgroups A and B of a group are commensurable when their intersection has finite index in each of them...
s. Other progress has been by arithmetic methods.
History
Nicholas Katz related some cases to deformation theoryDeformation theory
In mathematics, deformation theory is the study of infinitesimal conditions associated with varying a solution P of a problem to slightly different solutions Pε, where ε is a small number, or vector of small quantities. The infinitesimal conditions are therefore the result of applying the approach...
in 1972, in a paper where the conjecture was published. Since then, reformulations have been published. A q-analogue for difference equations has been proposed.
In responding to Kisin's talk on this work at the 2009 Colloque Grothendieck Katz gave a brief account from personal knowledge of the genesis of the conjecture. Grothendieck put it forth in public discussion in Spring 1969, but wrote nothing on the topic. He was led to the idea by foundational intuitions in the area of crystalline cohomology
Crystalline cohomology
In mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
, at that time being developed by his student Pierre Berthelot. In some way wishing to equate the notion of "nilpotence" in the theory of connections, with the divided power structure
Divided power structure
In mathematics, specifically commutative algebra, a divided power structure is a way of making expressions of the form x^n / n! meaningful even when it is not possible to actually divide by n!.- Definition :Let A be a commutative ring with an ideal I...
technique that became standard in crystalline theory, Grothendieck produced the conjecture as a by-product.
Further reading
- Jean-Benoît Bost, Algebraic leaves of algebraic foliations over number fields, Publications Mathématiques de L'IHÉS, Volume 93, Number 1, September 2001
- Yves André, Sur la conjecture des p-courbures de Grothendieck–Katz et un problème de Dwork, in Geometric Aspects of Dwork Theory (2004), editors Alan Adolphson, Francesco Baldassarri, Pierre Berthelot, Nicholas Katz, François Loeser
- Anand Pillay (2006), Differential algebra and generalizations of Grothendieck's conjecture on the arithmetic of linear differential equations

