Groundwater flow equation
Encyclopedia
Used in hydrogeology
, the groundwater flow equation is the mathematical
relationship which is used to describe the flow of groundwater
through an aquifer
. The transient flow of groundwater is described by a form of the diffusion equation, similar to that used in heat transfer
to describe the flow of heat in a solid (heat conduction
). The steady-state flow of groundwater is described by a form of the Laplace equation, which is a form of potential flow
and has analogs in numerous fields.
The groundwater flow equation is often derived for a small representative elemental volume (REV), where the properties of the medium are assumed to be effectively constant. A mass balance is done on the water flowing in and out of this small volume, the flux terms in the relationship being expressed in terms of head by using the constituitive equation
called Darcy's law
, which requires that the flow is slow.
, to arrive at the transient groundwater flow equation. This balance is analogous to the energy balance used in heat transfer
to arrive at the heat equation
. It is simply a statement of accounting, that for a given control volume, aside from sources or sinks, mass cannot be created or destroyed. The conservation of mass states that for a given increment of time (Δt) the difference between the mass flowing in across the boundaries, the mass flowing out across the boundaries, and the sources within the volume, is the change in storage.
times volume
, and under most conditions, water can be considered incompressible (density does not depend on pressure). The mass fluxes across the boundaries then become volume fluxes (as are found in Darcy's law
). Using Taylor series
to represent the in and out flux terms across the boundaries of the control volume, and using the divergence theorem
to turn the flux across the boundary into a flux over the entire volume, the final form of the groundwater flow equation (in differential form) is:
This is known in other fields as the diffusion equation or heat equation, it is a parabolic partial differential equation
(PDE). This mathematical statement indicates that the change in hydraulic head
with time (left hand side) equals the negative divergence
of the flux (q) and the source terms (G). This equation has both head and flux as unknowns, but Darcy's law relates flux to hydraulic heads, so substituting it in for the flux (q) leads to
Now if hydraulic conductivity
(k) is spatially uniform and isotropic (rather than a tensor
), it can be taken out of the spatial derivative, simplifying them to the Laplacian, this makes the equation
Dividing through by the specific storage
(Ss), puts hydraulic diffusivity (α = k/Ss or equivalently, α = T/S) on the right hand side. The hydraulic diffusivity is proportional to the speed at which a finite pressure pulse will propagate through the system (large values of α lead to fast propagation of signals). The groundwater flow equation then becomes
Where the sink/source term, G, now has the same units but is divided by the appropriate storage term (as defined by the hydraulic diffusivity substitution).
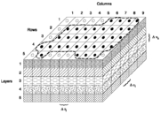
Especially when using rectangular grid finite-difference models (e.g. MODFLOW
, made by the USGS), we deal with Cartesian coordinates. In these coordinates the general Laplacian operator becomes (for three-dimensional flow) specifically
MODFLOW code discretizes and simulates an orthogonal 3-D form of the governing groundwater flow equation. However, it has an option to run in a "quasi-3D" mode if the user wishes to do so; in this case the model deals with the vertically averaged T and S, rather than k and Ss. In the quasi-3D mode, flow is calculated between 2D horizontal layers using the concept of leakage.
is a line source located at the origin — parallel to the z axis — causing converging radial flow). Under these conditions the above equation becomes (r being radial distance and θ being angle),
Despite these large assumptions, the groundwater flow equation does a good job of representing the distribution of heads in aquifers due to a transient distribution of sources and sinks.
This equation states that hydraulic head is a harmonic function
, and has many analogs in other fields. The Laplace equation can be solved using techniques, using similar assumptions stated above, but with the additional requirements of a steady-state flow field.
A common method for solution of this equations in civil engineering
and soil mechanics
is to use the graphical technique of drawing flownet
s; where contour line
s of hydraulic head and the stream function make a curvilinear grid, allowing complex geometries to be solved approximately.
Steady-state flow to a pumping well (which never truly occurs, but is sometimes a useful approximation) is commonly called the Thiem solution.
boundary condition: in addition to solving for the spatial distribution of heads, the location of this surface is also an unknown. This is a non-linear problem, even though the governing equation is linear.
An alternative formulation of the groundwater flow equation may be obtained by invoking the Dupuit assumption
(or Dupuit-Forcheimer assumption), where it is assumed that heads do not vary in the vertical direction (i.e.,
). A horizontal water balance is applied to a long vertical column with area 
extending from the aquifer base to the unsaturated surface. This distance is referred to as the saturated thickness, b. In a confined aquifer, the saturated thickness is determined by the height of the aquifer, H, and the pressure head is non-zero everywhere. In an unconfined aquifer
, the saturated thickness is defined as the vertical distance between the water table surface and the aquifer base. If
, and the aquifer base is at the zero datum, then the unconfined saturated thickness is equal to the head, i.e., b=h.
Assuming both the hydraulic conductivity
and the horizontal components of flow are uniform along the entire saturated thickness of the aquifer (i.e.,
and 
), we can express Darcy's law
in terms of integrated discharges, Qx and Qy:
Inserting these into our mass balance
expression, we obtain the general 2D governing equation for incompressible saturated groundwater flow:
Where n is the aquifer porosity
. The source term, N (length per time), represents the addition of water in the vertical direction (e.g., recharge). By incorporating the correct definitions for saturated thickness, specific storage
, and specific yield, we can transform this into two unique governing equations for confined and unconfined conditions:
(confined), where S=Ssb is the aquifer storativity and
(unconfined), where Sy is the specific yield of the aquifer.
Note that the partial differential equation
in the unconfined case is non-linear, whereas it is linear in the confined case. For unconfined steady-state flow, this non-linearity may be removed by expressing the PDE in terms of the head squared:
Or, for homogeneous aquifers,
This formulation allows us to apply standard methods for solving linear PDEs in the case of unconfined flow. For heterogeneous aquifers with no recharge, Potential flow
methods may be applied for mixed confined/unconfined cases.
Hydrogeology
Hydrogeology is the area of geology that deals with the distribution and movement of groundwater in the soil and rocks of the Earth's crust, . The term geohydrology is often used interchangeably...
, the groundwater flow equation is the mathematical
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
relationship which is used to describe the flow of groundwater
Groundwater
Groundwater is water located beneath the ground surface in soil pore spaces and in the fractures of rock formations. A unit of rock or an unconsolidated deposit is called an aquifer when it can yield a usable quantity of water. The depth at which soil pore spaces or fractures and voids in rock...
through an aquifer
Aquifer
An aquifer is a wet underground layer of water-bearing permeable rock or unconsolidated materials from which groundwater can be usefully extracted using a water well. The study of water flow in aquifers and the characterization of aquifers is called hydrogeology...
. The transient flow of groundwater is described by a form of the diffusion equation, similar to that used in heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
to describe the flow of heat in a solid (heat conduction
Heat conduction
In heat transfer, conduction is a mode of transfer of energy within and between bodies of matter, due to a temperature gradient. Conduction means collisional and diffusive transfer of kinetic energy of particles of ponderable matter . Conduction takes place in all forms of ponderable matter, viz....
). The steady-state flow of groundwater is described by a form of the Laplace equation, which is a form of potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
and has analogs in numerous fields.
The groundwater flow equation is often derived for a small representative elemental volume (REV), where the properties of the medium are assumed to be effectively constant. A mass balance is done on the water flowing in and out of this small volume, the flux terms in the relationship being expressed in terms of head by using the constituitive equation
Constitutive equation
In physics, a constitutive equation is a relation between two physical quantities that is specific to a material or substance, and approximates the response of that material to external forces...
called Darcy's law
Darcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
, which requires that the flow is slow.
Mass balance
A mass balance must be performed, and used along with Darcy's lawDarcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
, to arrive at the transient groundwater flow equation. This balance is analogous to the energy balance used in heat transfer
Heat transfer
Heat transfer is a discipline of thermal engineering that concerns the exchange of thermal energy from one physical system to another. Heat transfer is classified into various mechanisms, such as heat conduction, convection, thermal radiation, and phase-change transfer...
to arrive at the heat equation
Heat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
. It is simply a statement of accounting, that for a given control volume, aside from sources or sinks, mass cannot be created or destroyed. The conservation of mass states that for a given increment of time (Δt) the difference between the mass flowing in across the boundaries, the mass flowing out across the boundaries, and the sources within the volume, is the change in storage.
Diffusion equation (transient flow)
Mass can be represented as densityDensity
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
times volume
Volume
Volume is the quantity of three-dimensional space enclosed by some closed boundary, for example, the space that a substance or shape occupies or contains....
, and under most conditions, water can be considered incompressible (density does not depend on pressure). The mass fluxes across the boundaries then become volume fluxes (as are found in Darcy's law
Darcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
). Using Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
to represent the in and out flux terms across the boundaries of the control volume, and using the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
to turn the flux across the boundary into a flux over the entire volume, the final form of the groundwater flow equation (in differential form) is:
This is known in other fields as the diffusion equation or heat equation, it is a parabolic partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
(PDE). This mathematical statement indicates that the change in hydraulic head
Hydraulic head
Hydraulic head or piezometric head is a specific measurement of water pressure above a geodetic datum. It is usually measured as a water surface elevation, expressed in units of length, at the entrance of a piezometer...
with time (left hand side) equals the negative divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
of the flux (q) and the source terms (G). This equation has both head and flux as unknowns, but Darcy's law relates flux to hydraulic heads, so substituting it in for the flux (q) leads to
Now if hydraulic conductivity
Hydraulic conductivity
Hydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
(k) is spatially uniform and isotropic (rather than a tensor
Tensor
Tensors are geometric objects that describe linear relations between vectors, scalars, and other tensors. Elementary examples include the dot product, the cross product, and linear maps. Vectors and scalars themselves are also tensors. A tensor can be represented as a multi-dimensional array of...
), it can be taken out of the spatial derivative, simplifying them to the Laplacian, this makes the equation
Dividing through by the specific storage
Specific storage
Specific storage , storativity , specific yield and specific capacity are material physical properties that characterize the capacity of an aquifer to release groundwater from storage in response to a decline in hydraulic head. For that reason they are sometimes referred to as "storage properties"...
(Ss), puts hydraulic diffusivity (α = k/Ss or equivalently, α = T/S) on the right hand side. The hydraulic diffusivity is proportional to the speed at which a finite pressure pulse will propagate through the system (large values of α lead to fast propagation of signals). The groundwater flow equation then becomes
Where the sink/source term, G, now has the same units but is divided by the appropriate storage term (as defined by the hydraulic diffusivity substitution).
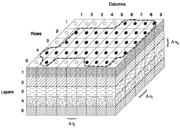
Rectangular cartesian coordinates
MODFLOW
MODFLOW is the U.S. Geological Survey modular finite-difference flow model, which is a computer code that solves the groundwater flow equation. The program is used by hydrogeologists to simulate the flow of groundwater through aquifers...
, made by the USGS), we deal with Cartesian coordinates. In these coordinates the general Laplacian operator becomes (for three-dimensional flow) specifically
MODFLOW code discretizes and simulates an orthogonal 3-D form of the governing groundwater flow equation. However, it has an option to run in a "quasi-3D" mode if the user wishes to do so; in this case the model deals with the vertically averaged T and S, rather than k and Ss. In the quasi-3D mode, flow is calculated between 2D horizontal layers using the concept of leakage.
Circular cylindrical coordinates
Another useful coordinate system is 3D cylindrical coordinates (typically where a pumping wellWater well
A water well is an excavation or structure created in the ground by digging, driving, boring or drilling to access groundwater in underground aquifers. The well water is drawn by an electric submersible pump, a trash pump, a vertical turbine pump, a handpump or a mechanical pump...
is a line source located at the origin — parallel to the z axis — causing converging radial flow). Under these conditions the above equation becomes (r being radial distance and θ being angle),
Assumptions
This equation represents flow to a pumping well (a sink of strength G), located at the origin. Both this equation and the Cartesian version above are the fundamental equation in groundwater flow, but to arrive at this point requires considerable simplification. Some of the main assumptions which went into both these equations are:- the aquifer material is incompressible (no change in matrix due to changes in pressure — aka subsidence),
- the water is of constant density (incompressible),
- any external loads on the aquifer (e.g., overburdenOverburdenOverburden is the material that lies above an area of economic or scientific interest in mining and archaeology; most commonly the rock, soil, and ecosystem that lies above a coal seam or ore body. It is also known as 'waste' or 'spoil'...
, atmospheric pressureAtmospheric pressureAtmospheric pressure is the force per unit area exerted into a surface by the weight of air above that surface in the atmosphere of Earth . In most circumstances atmospheric pressure is closely approximated by the hydrostatic pressure caused by the weight of air above the measurement point...
) are constant, - for the 1D radial problem the pumping well is fully penetrating a non-leaky aquifer,
- the groundwater is flowing slowly (Reynolds number less than unity), and
- the hydraulic conductivity (k) is an isotropic scalarScalar (physics)In physics, a scalar is a simple physical quantity that is not changed by coordinate system rotations or translations , or by Lorentz transformations or space-time translations . This is in contrast to a vector...
.
Despite these large assumptions, the groundwater flow equation does a good job of representing the distribution of heads in aquifers due to a transient distribution of sources and sinks.
Laplace equation (steady-state flow)
If the aquifer has recharging boundary conditions a steady-state may be reached (or it may be used as an approximation in many cases), and the diffusion equation (above) simplifies to the Laplace equation.
This equation states that hydraulic head is a harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
, and has many analogs in other fields. The Laplace equation can be solved using techniques, using similar assumptions stated above, but with the additional requirements of a steady-state flow field.
A common method for solution of this equations in civil engineering
Civil engineering
Civil engineering is a professional engineering discipline that deals with the design, construction, and maintenance of the physical and naturally built environment, including works like roads, bridges, canals, dams, and buildings...
and soil mechanics
Soil mechanics
Soil mechanics is a branch of engineering mechanics that describes the behavior of soils. It differs from fluid mechanics and solid mechanics in the sense that soils consist of a heterogeneous mixture of fluids and particles but soil may also contain organic solids, liquids, and gasses and other...
is to use the graphical technique of drawing flownet
Flownet
A flownet is a graphical representation of two-dimensional steady-state groundwater flow through aquifers. Construction of a flownet is often used for solving groundwater flow problems where the geometry makes analytical solutions impractical...
s; where contour line
Contour line
A contour line of a function of two variables is a curve along which the function has a constant value. In cartography, a contour line joins points of equal elevation above a given level, such as mean sea level...
s of hydraulic head and the stream function make a curvilinear grid, allowing complex geometries to be solved approximately.
Steady-state flow to a pumping well (which never truly occurs, but is sometimes a useful approximation) is commonly called the Thiem solution.
Two-dimensional groundwater flow
The above groundwater flow equations are valid for three dimensional flow. In unconfined aquifers, the solution to the 3D form of the equation is complicated by the presence of a free surface water tableWater table
The water table is the level at which the submarine pressure is far from atmospheric pressure. It may be conveniently visualized as the 'surface' of the subsurface materials that are saturated with groundwater in a given vicinity. However, saturated conditions may extend above the water table as...
boundary condition: in addition to solving for the spatial distribution of heads, the location of this surface is also an unknown. This is a non-linear problem, even though the governing equation is linear.
An alternative formulation of the groundwater flow equation may be obtained by invoking the Dupuit assumption
Dupuit assumption
The Dupuit assumption holds that groundwater moves horizontally in an unconfined aquifer, and that the groundwater discharge is proportional to the saturated aquifer thickness...
(or Dupuit-Forcheimer assumption), where it is assumed that heads do not vary in the vertical direction (i.e.,
). A horizontal water balance is applied to a long vertical column with area extending from the aquifer base to the unsaturated surface. This distance is referred to as the saturated thickness, b. In a confined aquifer, the saturated thickness is determined by the height of the aquifer, H, and the pressure head is non-zero everywhere. In an unconfined aquiferAquifer
An aquifer is a wet underground layer of water-bearing permeable rock or unconsolidated materials from which groundwater can be usefully extracted using a water well. The study of water flow in aquifers and the characterization of aquifers is called hydrogeology...
, the saturated thickness is defined as the vertical distance between the water table surface and the aquifer base. If
, and the aquifer base is at the zero datum, then the unconfined saturated thickness is equal to the head, i.e., b=h.Assuming both the hydraulic conductivity
Hydraulic conductivity
Hydraulic conductivity, symbolically represented as K, is a property of vascular plants, soil or rock, that describes the ease with which water can move through pore spaces or fractures. It depends on the intrinsic permeability of the material and on the degree of saturation...
and the horizontal components of flow are uniform along the entire saturated thickness of the aquifer (i.e.,
and ), we can express Darcy's lawDarcy's law
Darcy's law is a phenomenologically derived constitutive equation that describes the flow of a fluid through a porous medium. The law was formulated by Henry Darcy based on the results of experiments on the flow of water through beds of sand...
in terms of integrated discharges, Qx and Qy:
Inserting these into our mass balance
Mass balance
A mass balance is an application of conservation of mass to the analysis of physical systems. By accounting for material entering and leaving a system, mass flows can be identified which might have been unknown, or difficult to measure without this technique...
expression, we obtain the general 2D governing equation for incompressible saturated groundwater flow:
Where n is the aquifer porosity
Porosity
Porosity or void fraction is a measure of the void spaces in a material, and is a fraction of the volume of voids over the total volume, between 0–1, or as a percentage between 0–100%...
. The source term, N (length per time), represents the addition of water in the vertical direction (e.g., recharge). By incorporating the correct definitions for saturated thickness, specific storage
Specific storage
Specific storage , storativity , specific yield and specific capacity are material physical properties that characterize the capacity of an aquifer to release groundwater from storage in response to a decline in hydraulic head. For that reason they are sometimes referred to as "storage properties"...
, and specific yield, we can transform this into two unique governing equations for confined and unconfined conditions:
(confined), where S=Ssb is the aquifer storativity and
(unconfined), where Sy is the specific yield of the aquifer.
Note that the partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in the unconfined case is non-linear, whereas it is linear in the confined case. For unconfined steady-state flow, this non-linearity may be removed by expressing the PDE in terms of the head squared:
Or, for homogeneous aquifers,
This formulation allows us to apply standard methods for solving linear PDEs in the case of unconfined flow. For heterogeneous aquifers with no recharge, Potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
methods may be applied for mixed confined/unconfined cases.
See also
- Analytic element methodAnalytic element methodThe analytic element method is a numerical method used for the solution of partial differential equations. It was initially developed by O.D.L. Strack at the University of Minnesota...
, a numerical method used for the solution of partial differential equations - Dupuit assumptionDupuit assumptionThe Dupuit assumption holds that groundwater moves horizontally in an unconfined aquifer, and that the groundwater discharge is proportional to the saturated aquifer thickness...
, a simplification of the groundwater flow equation regarding vertical flow - Groundwater energy balanceGroundwater energy balanceThe groundwater energy balance is the energy balance of a groundwater body in terms of incoming hydraulic energy associated with groundwater inflow into the body, energy associated with the outflow, energy conversion into heat due to friction of flow, and the resulting change of energy status and...
, groundwater flow equations based on the energy balance
Further reading
- An excellent beginner's read for groundwater modeling. Covers all the basic concepts, with simple examples in FORTRAN 77.
External links
- USGS groundwater software — free groundwater modeling software like MODFLOW