
Hedgehog space
Encyclopedia
In mathematics
, a hedgehog space is a topological space
, consisting of a set of spines joined at a point.
For any cardinal number
 , the
, the  -hedgehog space is formed by taking the disjoint union
-hedgehog space is formed by taking the disjoint union
of real unit interval
real unit interval
s identified at the origin. Each unit interval is referred to as one of the hedgehog's spines. A -hedgehog space is sometimes called a hedgehog space of spininess
-hedgehog space is sometimes called a hedgehog space of spininess  .
.
The hedgehog space is a metric space
, when endowed with the hedgehog metric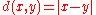 if
if  and
and  lie in the same spine, and by
lie in the same spine, and by 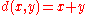 if
if  and
and 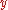 lie in different spines. Although their disjoint union makes the origins of the intervals distinct, the metric identifies them by assigning them 0 distance.
lie in different spines. Although their disjoint union makes the origins of the intervals distinct, the metric identifies them by assigning them 0 distance.
Hedgehog spaces are examples of real tree
s.
when the two points belong to a ray though the origin, and is otherwise the sum of the distances of the two points from the origin, is sometimes called the Paris metric because navigation in this metric resembles that in the radial street plan of Paris
. The Paris metric, restricted to the unit disk, is a hedgehog space where K is the cardinality of the continuum
.
 can be represented as a subspace of the product of countably many
can be represented as a subspace of the product of countably many  -hedgehog spaces.
-hedgehog spaces.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a hedgehog space is a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
, consisting of a set of spines joined at a point.
For any cardinal number
Cardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
 , the
, the  -hedgehog space is formed by taking the disjoint union
-hedgehog space is formed by taking the disjoint unionDisjoint union
In mathematics, the term disjoint union may refer to one of two different concepts:* In set theory, a disjoint union is a modified union operation that indexes the elements according to which set they originated in; disjoint sets have no element in common.* In probability theory , a disjoint union...
of
 real unit interval
real unit intervalUnit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...
s identified at the origin. Each unit interval is referred to as one of the hedgehog's spines. A
 -hedgehog space is sometimes called a hedgehog space of spininess
-hedgehog space is sometimes called a hedgehog space of spininess  .
.The hedgehog space is a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, when endowed with the hedgehog metric
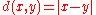 if
if  and
and  lie in the same spine, and by
lie in the same spine, and by 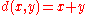 if
if  and
and 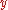 lie in different spines. Although their disjoint union makes the origins of the intervals distinct, the metric identifies them by assigning them 0 distance.
lie in different spines. Although their disjoint union makes the origins of the intervals distinct, the metric identifies them by assigning them 0 distance.Hedgehog spaces are examples of real tree
Real tree
A real tree, or an \mathbb R-tree, is a metric space such thatfor any x, y in M there is a unique arc from x to y and this arc is a geodesic segment. Here by an arc from x to y we mean the image in M of a topological embedding f from an interval [a,b] to M such that f=x and f=y...
s.
Paris metric
The metric on the plane in which the distance between any two points is their Euclidean distanceEuclidean distance
In mathematics, the Euclidean distance or Euclidean metric is the "ordinary" distance between two points that one would measure with a ruler, and is given by the Pythagorean formula. By using this formula as distance, Euclidean space becomes a metric space...
when the two points belong to a ray though the origin, and is otherwise the sum of the distances of the two points from the origin, is sometimes called the Paris metric because navigation in this metric resembles that in the radial street plan of Paris
Paris
Paris is the capital and largest city in France, situated on the river Seine, in northern France, at the heart of the Île-de-France region...
. The Paris metric, restricted to the unit disk, is a hedgehog space where K is the cardinality of the continuum
Cardinality of the continuum
In set theory, the cardinality of the continuum is the cardinality or “size” of the set of real numbers \mathbb R, sometimes called the continuum. It is an infinite cardinal number and is denoted by |\mathbb R| or \mathfrak c ....
.
Kowalsky's theorem
Kowalsky's theorem states that any metric space of weight can be represented as a subspace of the product of countably many
can be represented as a subspace of the product of countably many  -hedgehog spaces.
-hedgehog spaces.

